2018-2019学年浙江省杭州市萧山区城厢片九年级(下)期初数学试卷解析版
文档属性
| 名称 | 2018-2019学年浙江省杭州市萧山区城厢片九年级(下)期初数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 167.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-01 00:00:26 | ||
图片预览


文档简介
2018-2019学年浙江省杭州市萧山区城厢片九年级(下)期初数学试卷
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项最符合题目要求.
1.下列事件中,属于必然事件的是( )
A.旭日东升 B.守株待兔 C.大海捞针 D.明天放假
2.二次函数y=(x+1)2与x轴交点坐标为( )
A.(﹣1,0) B.(1,0) C.(0,﹣1) D.(0,1)
3.已知在Rt△ABC中,∠C=90°,∠A=α,BC=m,那么AB的长为( )
A.msinα B.mcosα C. D.
4.点P是半径为10的圆O所在平面上的一点,且点P到点O的距离为8.则过点P的直线l与圆O的位置关系为( )
A.相交
B.相切
C.相离
D.相交、相切、相离都有可能
5.如果一个扇形的半径是3,弧长是π,那么此扇形的圆心角的大小为( )
A.30° B.45° C.60° D.90°
6.如图,AB是半圆O的直径,D为半圆上的点,在BA延长线上取点C,使得DC=DO,连结CD并延长交圆O于点E,连结AE,若∠C=18°,则∠EAB的度数为( )
A.18° B.21° C.27° D.36°
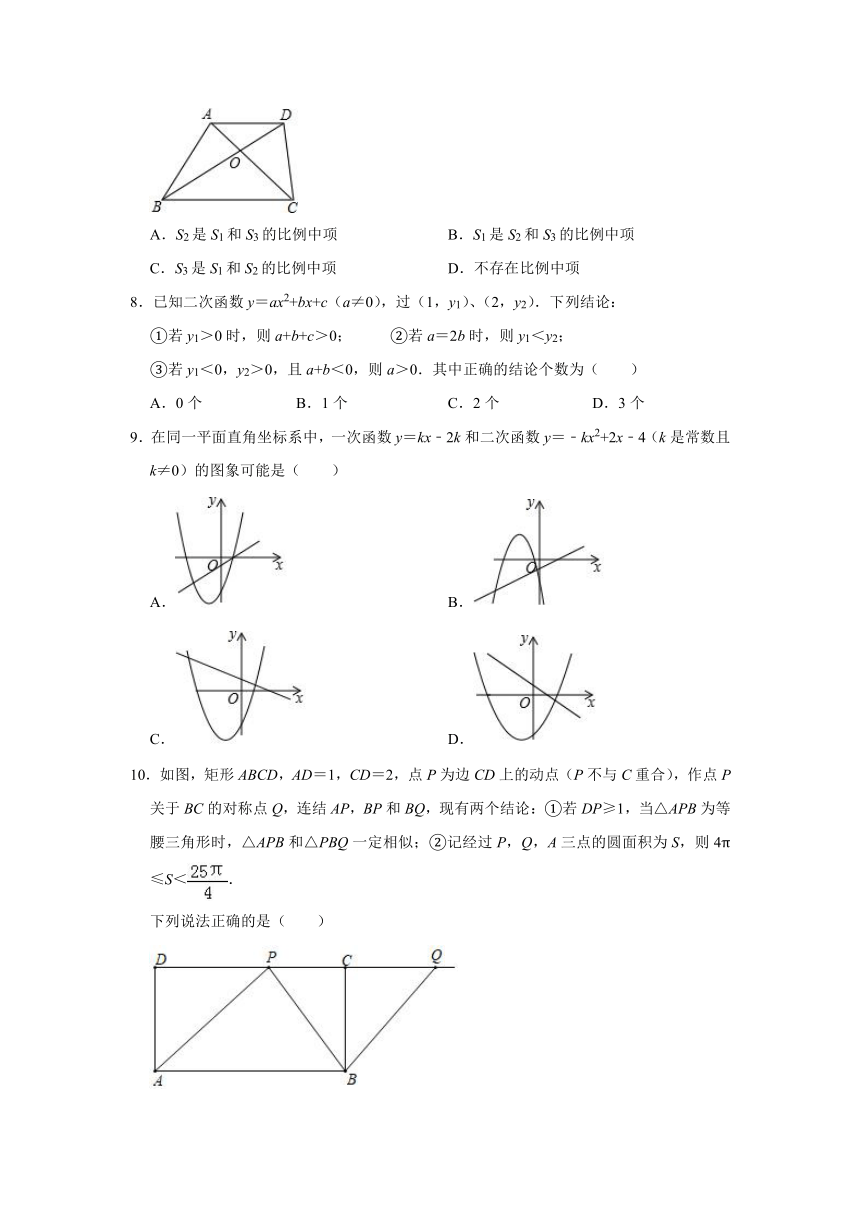
7.如图,四边形ABCD中,AD∥BC,AC和BD交于点O,记S△AOD为S1,S△AOB为S2,S△BOC为S3,则下列关于比例中项的描述正确的是( )
A.S2是S1和S3的比例中项 B.S1是S2和S3的比例中项
C.S3是S1和S2的比例中项 D.不存在比例中项
8.已知二次函数y=ax2+bx+c(a≠0),过(1,y1)、(2,y2).下列结论:
①若y1>0时,则a+b+c>0; ②若a=2b时,则y1<y2;
③若y1<0,y2>0,且a+b<0,则a>0.其中正确的结论个数为( )
A.0个 B.1个 C.2个 D.3个
9.在同一平面直角坐标系中,一次函数y=kx﹣2k和二次函数y=﹣kx2+2x﹣4(k是常数且k≠0)的图象可能是( )
A. B.
C. D.
10.如图,矩形ABCD,AD=1,CD=2,点P为边CD上的动点(P不与C重合),作点P关于BC的对称点Q,连结AP,BP和BQ,现有两个结论:①若DP≥1,当△APB为等腰三角形时,△APB和△PBQ一定相似;②记经过P,Q,A三点的圆面积为S,则4π≤S<.
下列说法正确的是( )
A.①对②对 B.①对②错 C.①错②对 D.①错②错
二、填空题:本题有6个小题,每小题4分,共24分.
11.(4分)比较大小:cos30° .
12.(4分)一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于,问至少取出了 个黑球.
13.(4分)已知关于x的一元二次方程x2+bx﹣c=0无实数解,则抛物线y=﹣x2﹣bx+c经过 象限.
14.(4分)如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是 .
15.(4分)将抛物线y1=x2﹣2x﹣3先向左平移1个单位,再向上平移4个单位后,与抛物线y2=ax2+bx+c重合,现有一直线y3=2x+3与抛物线y2=ax2+bx+c相交.当y2≤y3时自变量x的取值范围是 .
16.(4分)如图所示,在△ABD中,BC为AD边上的高线,tan∠BAD=1,在BC上截取CG=CD,连结AG,将△ACG绕点C旋转,使点G落在BD边上的F处,A落在E处,连结BE,若AD=4,tanD=3,则△CFD和△ECF的面积比为 ;BE长为 .
三、解答题:本题有7小题,共66分.解答应写出文字说明、证明过程或演算步骤.
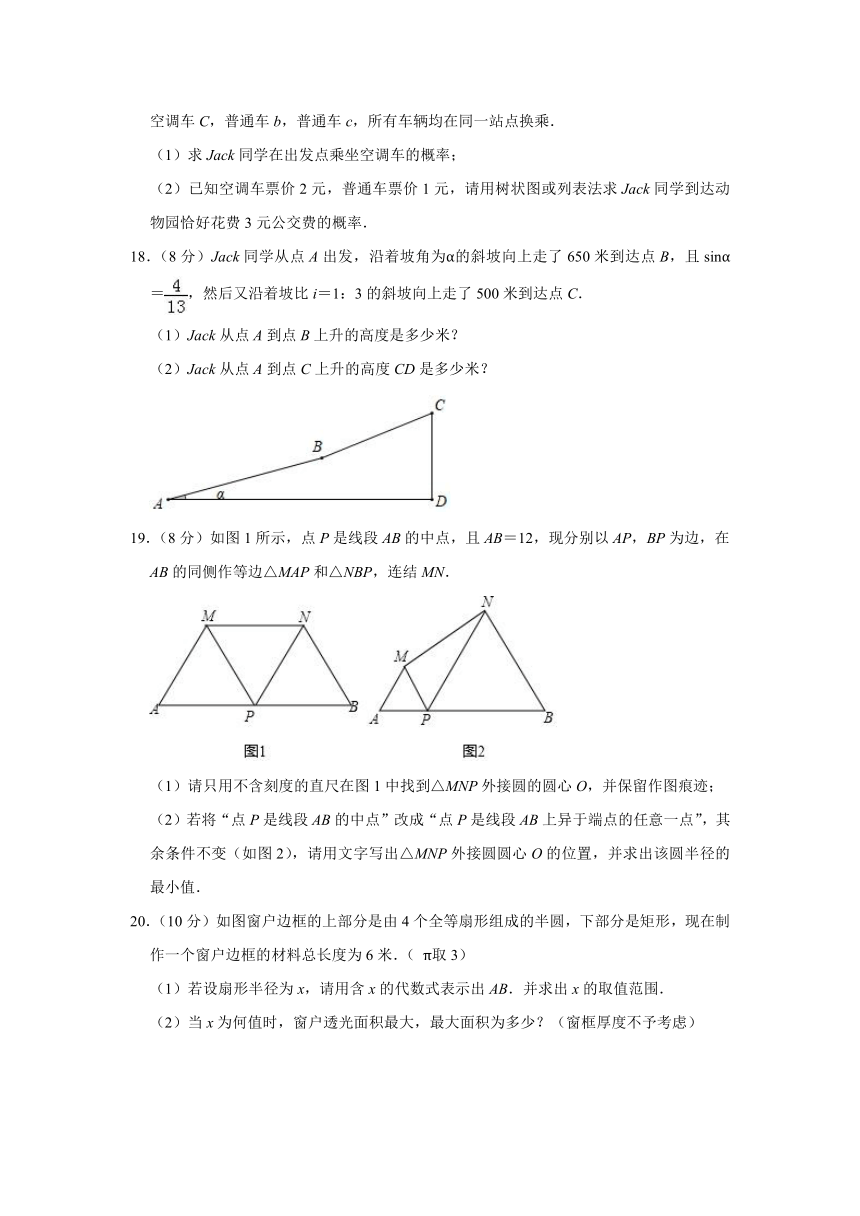
17.(6分)Jack同学寒假去野生动物园游玩,从Baidu地图查找线路发现,几条线路均要换乘,乘车方案如下:在出发站点可选择空调车A,空调车B,普通车a;换乘点可选择空调车C,普通车b,普通车c,所有车辆均在同一站点换乘.
(1)求Jack同学在出发点乘坐空调车的概率;
(2)已知空调车票价2元,普通车票价1元,请用树状图或列表法求Jack同学到达动物园恰好花费3元公交费的概率.
18.(8分)Jack同学从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=,然后又沿着坡比i=1:3的斜坡向上走了500米到达点C.
(1)Jack从点A到点B上升的高度是多少米?
(2)Jack从点A到点C上升的高度CD是多少米?
19.(8分)如图1所示,点P是线段AB的中点,且AB=12,现分别以AP,BP为边,在AB的同侧作等边△MAP和△NBP,连结MN.
(1)请只用不含刻度的直尺在图1中找到△MNP外接圆的圆心O,并保留作图痕迹;
(2)若将“点P是线段AB的中点”改成“点P是线段AB上异于端点的任意一点”,其余条件不变(如图2),请用文字写出△MNP外接圆圆心O的位置,并求出该圆半径的最小值.
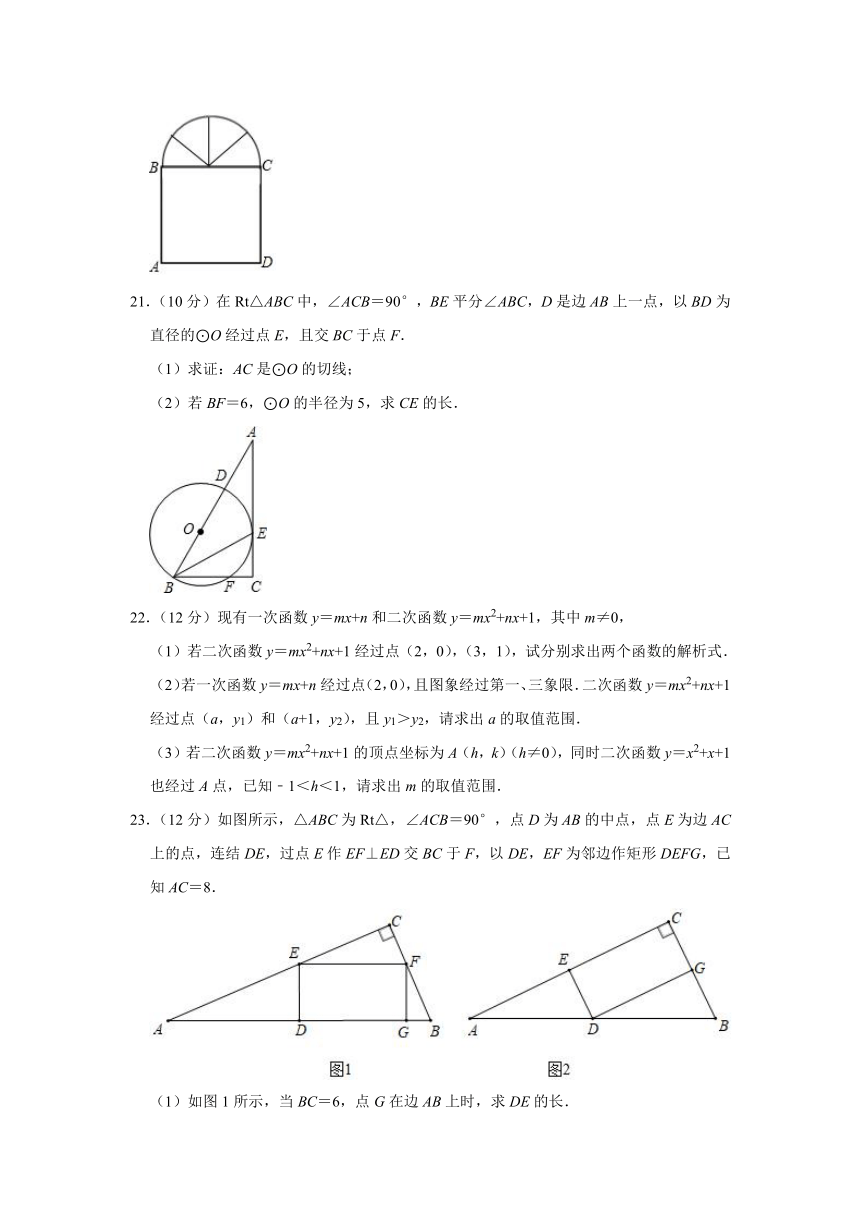
20.(10分)如图窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形,现在制作一个窗户边框的材料总长度为6米.( π取3)
(1)若设扇形半径为x,请用含x的代数式表示出AB.并求出x的取值范围.
(2)当x为何值时,窗户透光面积最大,最大面积为多少?(窗框厚度不予考虑)
21.(10分)在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
22.(12分)现有一次函数y=mx+n和二次函数y=mx2+nx+1,其中m≠0,
(1)若二次函数y=mx2+nx+1经过点(2,0),(3,1),试分别求出两个函数的解析式.
(2)若一次函数y=mx+n经过点(2,0),且图象经过第一、三象限.二次函数y=mx2+nx+1经过点(a,y1)和(a+1,y2),且y1>y2,请求出a的取值范围.
(3)若二次函数y=mx2+nx+1的顶点坐标为A(h,k)(h≠0),同时二次函数y=x2+x+1也经过A点,已知﹣1<h<1,请求出m的取值范围.
23.(12分)如图所示,△ABC为Rt△,∠ACB=90°,点D为AB的中点,点E为边AC上的点,连结DE,过点E作EF⊥ED交BC于F,以DE,EF为邻边作矩形DEFG,已知AC=8.
(1)如图1所示,当BC=6,点G在边AB上时,求DE的长.
(2)如图2所示,若,点G在边BC上时,求BC的长.
(3)①若,且点G恰好落在Rt△ABC的边上,求BC的长.
②若(n为正整数),且点G恰好落在Rt△ABC的边上,请直接写出BC的长.
2018-2019学年浙江省杭州市萧山区城厢片九年级(下)期初数学试卷
参考答案与试题解析
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项最符合题目要求.
1.【解答】解:A、旭日东升是必然事件,正确;
B、守株待兔是随机事件,不符合题意;
C、大海捞针是不可能事件,不符合题意;
D、明天放假是随机事件,不符合题意;
故选:A.
2.【解答】解:二次函数y=(x+1)2图象与x轴交点横坐标就是(x+1)2=0的根,
解方程(x+1)2=0,
得:x1=x2=﹣1,
∴二次函数y=(x+1)2图象与x轴交点坐标为(﹣1,0);
故选:A.
3.【解答】
解:在Rt△ACB中,BC=m,∠A=α,
∴sinA=,
∴AB==,
故选:C.
4.【解答】解:∵点P到点O的距离为8,圆O的半径为10,
∴8<10,
∴点P在圆内,
∴过点P的直线l与圆O的位置关系为相交,
故选:A.
5.【解答】解:设圆心角为n°.
由题意:=π,
∴n=60,
故选:C.
6.【解答】解:如图,连接OE,
∵DC=DO,
∴∠DOC=∠C=18°,
∴∠ODE=∠DOC+∠C=36°,
∵OD=OE,
∴∠OED=∠ODE=36°,
∴∠EOB=∠C+∠OED=18°+36°=54°,
∴∠EAB=∠EOB=27°,
故选:C.
7.【解答】解:∵AD∥BC,
∴△AOD∽△COB,
∴=()2,
∵=,
∴=()2,
∴S22=S1?S3,
即S2是S1和S3的比例中项.
故选:A.
8.【解答】解:①将点(1,y1)代入二次函数y=ax2+bx+c,
得到y1=a+b+c,
∵y1>0,
∴a+b+c>0.
故①正确.
②若a=2b时,函数对称轴x=﹣=﹣,
当a>0时,y1<y2,
当a<0时,y1>y2.
故②错误.
③∵a+b<0,
∴a<﹣b
当a<0时,﹣<,此时只能y1>0,y2<0;
当a>0时,﹣>,此时只能y1<0,y2>0;
所以y1<0,y2>0,且a+b<0时,a>0.
故③正确.
故选:C.
9.【解答】解:A、由一次函数图象可知,k>0,∴﹣k<0,∴二次函数的图象开口应该向下,故A选项不合题意;
B、由一次函数图象可知,k>0,∴﹣k<0,,∴二次函数的图象开口向下,且对称轴在x轴的正半轴,故B选项不合题意;
C、由一次函数图象可知,k<0,∴﹣k>0,,∴二次函数的图象开口向上,且对称轴在x轴的负半轴,一次函数必经过点(2,0),当x=2时,二次函数值y=﹣4k>0,故C选项符合题意;
D、由一次函数图象可知,k<0,∴﹣k>0,,∴二次函数的图象开口向上,且对称轴在x轴的负半轴,一次函数必经过点(2,0),当x=2时,二次函数值y=﹣4k>0,故D选项不合题意;
故选:C.
10.【解答】解:①如图1中,
∵DP≥1,当△APB为等腰三角形,
∴只有AP=AB,
在Rt△ADP中,∵∠D=90°,AP=2,AD=1,
∴PA=2AD,
∴∠APD=30°,
∵CD∥AB,
∴∠CPB=∠ABP,
∵AP=AB,
∴∠ABP=∠APB,
∴∠APB=∠CPB=75°,
∵P,Q关于BC对称,
∴BP=BQ,
∴∠BPC=∠BQC=75°,
∴△APB∽△BPQ,故①正确.
②如图2中,作△APQ的外接圆⊙O.
当点O与B重合时,⊙O的半径最小,此时⊙O的面积为4π,
当点P与C重合时,设OA=OP=x,
在Rt△AOB中,则有x2=22+(x﹣1)2,
∴x=,
此时⊙O的面积=π,
观察图象可知:4π≤S<.故②正确,
故选:A.
二、填空题:本题有6个小题,每小题4分,共24分.
11.【解答】解:∵cos30°=,
∴cos30°>.
故答案为:>.
12.【解答】解:设取走x个黑球,则放入x个黄球,
由题意,得≥,
解得:x≥,
∵x为整数,
∴x的最小正整数解是x=9.
答:至少取走了9个黑球.
故答案为:9.
13.【解答】解:∵关于x的一元二次方程x2+bx﹣c=0无实数解,
∴△=b2+4c<0,
∵抛物线y=﹣x2﹣bx+c中,二次项系数﹣1<0,
∴抛物线的开口向下,
∵判别式=(﹣b)2﹣4×(﹣1)×c=b2+4c<0,
∴抛物线与x轴无交点,
∴抛物线在x轴的下方,
∴抛物线y=﹣x2﹣bx+c经过第三、四象限;
故答案为:三、四.
14.【解答】解:
当O、Q、P三点一线且OP⊥BC时,PQ有最小值,设AC与圆的切点为D,连接OD,如图,
∵AC为圆的切线,
∴OD⊥AC,
∵AC=8,BC=6,AB=10,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴OD∥BC,且O为AB中点,
∴OD为△ABC的中位线,
∴OD=BC=3,
同理可得PO=AC=4,
∴PQ=OP﹣OQ=4﹣3=1,
故答案为:1.
15.【解答】解:y1=x2﹣2x﹣3=(x﹣1)2﹣4,
把y1=(x﹣1)2﹣4先向左平移1个单位,再向上平移4个单位后所得抛物线解析式为y=x2,
解方程组得或,
所以直线y3=2x+3与抛物线y2=ax2+bx+c交点坐标为(﹣1,1),(3,9),
当﹣1≤x≤3时,y2≤y3.
故答案为﹣1≤x≤3.
16.【解答】解:作CM⊥DF于M,如图所示:
则∠CMD=90°,
∵在△ABD中,BC为AD边上的高线,tan∠BAD=1,
∴∠BCD=∠ACB=90°,AC=BC,
在Rt△BCD中,∵tanD=3=,
∴BC=3CD,
∵AD=AC+CD=BC+CD=4,
∴CD=1,AC=BC=3,
∵∠CMD=∠BCD,∠D=∠D,
∴△CDM∽△BDC,==,
∴=,
在△AGC和△BDC中,,
∴△AGC≌△BDC(SAS),
∴∠CAG=∠CBD,△AGC的面积=△BDC的面积,∠CAG=∠CBD,
由旋转的性质得:CF=CD,EC=AC=BC,∠CEF=∠CAG,∠BCF=∠ACN,
∴△CDF的面积=2△CDM的面积,
∴△CFD的面积:△ECF的面积=1:5;
∵CG=CD,
∴CG=CF,
在△ACN和△BCF中,,
∴△ACN≌△BCF(ASA),
∴AN=BF,CN=CF=CD=CG=1,
∴GN=DF,BC:CG=CE:CN,
∵∠GCN=∠BCE,
∴△CGN∽△CBE,
∴=,
在Rt△DCM中,tanD=3,CD=1,
∴DM=,
∵CD=CF,CM⊥DF,
∴DF=2DM=,
∴GN=,
∴=,
解得:BE=;
故答案为:1:5,.
三、解答题:本题有7小题,共66分.解答应写出文字说明、证明过程或演算步骤.
17.【解答】解:(1)∵在出发站点可选择空调车A、空调车B、普通车a,
∴Jack在出发站点乘坐空调车的概率为:;
(2)如图所示:
,
一共有9种组合,只有Ab,Ac,Bb,Bc,aC组合恰好花费3元,
故Jack到达动物园恰好花费3元公交费的概率为:.
18.【解答】解:(1)作BF⊥AD
在Rt△ABF中,BF=AB×sinα=650×=200(米),
答:Jack从点A到点B上升的高度是200米;
(2)作BE⊥CD
在Rt△CBE中,CE:BE=1:3,
可得CE:BC=1:,
可得CE=,
得CD=(200+50)m,
答:Jack从点A到点C上升的高度CD是(200+50)米.
19.【解答】解:(1)如图,连接AN,BM交于点O,点O即为所求.
(2)O点为∠MAB角平分线和∠NBA角平分线的交点.
当OP⊥AB时,半径最短,
可得r=.
20.【解答】解:(1)根据题意得:2AB+7x+πx=2AB+10x=6,
整理得:AB=3﹣5x;
根据3﹣5x>0,
所以x的取值范围是:0<x<;
(2)设面积为S,则S=2x(3﹣5x)+x2=﹣x2+6x=﹣(x﹣)2+,
当x=时,S最大=.
21.【解答】(1)证明:连接OE.
∵OE=OB,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBC,
∴∠EBC=∠OEB,
∴OE∥BC,
∴∠OEA=∠C,
∵∠ACB=90°,
∴∠OEA=90°
∴AC是⊙O的切线;
(2)解:连接OE、OF,过点O作OH⊥BF交BF于H,
由题意可知四边形OECH为矩形,
∴OH=CE,
∵BF=6,
∴BH=3,
在Rt△BHO中,OB=5,
∴OH==4,
∴CE=4.
22.【解答】解:(1)将点(2,0),(3,1),代入一次函数y=mx+n中,
,
解得,
∴一次函数的解析式是y=x﹣2,
再将点(2,0),(3,1),代入二次函数y=mx2+nx+1,
,
解得,
∴二次函数的解析式是y═x2++1.
(2)∵一次函数y=mx+n经过点(2,0),
∴n=﹣2m,
∵二次函数y=mx2+nx+1的对称轴是x=﹣,
∴对称轴为x=1,
又∵一次函数y=mx+n图象经过第一、三象限,
∴m>0,
∵y1>y2,
∴1﹣a>1+a﹣1,
∴a<.
(3)∵y=mx2+nx+1的顶点坐标为A(h,k),
∴k=mh2+nh+1,且h=﹣,
又∵二次函数y=x2+x+1也经过A点,
∴k=h2+h+1,
∴mh2+nh+1=h2+h+1,
∴,
又∵﹣1<h<1,
∴m<﹣2或m>0.
23.【解答】解:(1)如图1中,
在Rt△ABC中,∵AC=8,BC=6,
∴AB===10,
∵D是AB中点,
∴AD=DB=5,
∵∠A=∠A,
∴tan∠A==,
∴=,
∴DE=.
(2)如图2中,设DE=x,则EF=EC=2x.
∵DE∥BC,AD=DB,
∴AE=EC=2x,
∴4x=8,
∴x=2,
∴DE=BC,
∴BC=2DE=4.
(3)①当点G落在BC边上时,如图2中,设DE=x,则EF=EC=4x,
可得:AE=EC=4x,8x=8,
∴x=1,
∴BC=2DE=2.
当点G落在AB边上时,
作DH⊥AC于H,设DH=x,则CE=4x,BC=2x,EH=4﹣4x,
利用△HDE∽△CAB,可得,解得x=,则BC=.
②若(n为正整数)时,同法可知:BC=或.
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项最符合题目要求.
1.下列事件中,属于必然事件的是( )
A.旭日东升 B.守株待兔 C.大海捞针 D.明天放假
2.二次函数y=(x+1)2与x轴交点坐标为( )
A.(﹣1,0) B.(1,0) C.(0,﹣1) D.(0,1)
3.已知在Rt△ABC中,∠C=90°,∠A=α,BC=m,那么AB的长为( )
A.msinα B.mcosα C. D.
4.点P是半径为10的圆O所在平面上的一点,且点P到点O的距离为8.则过点P的直线l与圆O的位置关系为( )
A.相交
B.相切
C.相离
D.相交、相切、相离都有可能
5.如果一个扇形的半径是3,弧长是π,那么此扇形的圆心角的大小为( )
A.30° B.45° C.60° D.90°
6.如图,AB是半圆O的直径,D为半圆上的点,在BA延长线上取点C,使得DC=DO,连结CD并延长交圆O于点E,连结AE,若∠C=18°,则∠EAB的度数为( )
A.18° B.21° C.27° D.36°
7.如图,四边形ABCD中,AD∥BC,AC和BD交于点O,记S△AOD为S1,S△AOB为S2,S△BOC为S3,则下列关于比例中项的描述正确的是( )
A.S2是S1和S3的比例中项 B.S1是S2和S3的比例中项
C.S3是S1和S2的比例中项 D.不存在比例中项
8.已知二次函数y=ax2+bx+c(a≠0),过(1,y1)、(2,y2).下列结论:
①若y1>0时,则a+b+c>0; ②若a=2b时,则y1<y2;
③若y1<0,y2>0,且a+b<0,则a>0.其中正确的结论个数为( )
A.0个 B.1个 C.2个 D.3个
9.在同一平面直角坐标系中,一次函数y=kx﹣2k和二次函数y=﹣kx2+2x﹣4(k是常数且k≠0)的图象可能是( )
A. B.
C. D.
10.如图,矩形ABCD,AD=1,CD=2,点P为边CD上的动点(P不与C重合),作点P关于BC的对称点Q,连结AP,BP和BQ,现有两个结论:①若DP≥1,当△APB为等腰三角形时,△APB和△PBQ一定相似;②记经过P,Q,A三点的圆面积为S,则4π≤S<.
下列说法正确的是( )
A.①对②对 B.①对②错 C.①错②对 D.①错②错
二、填空题:本题有6个小题,每小题4分,共24分.
11.(4分)比较大小:cos30° .
12.(4分)一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于,问至少取出了 个黑球.
13.(4分)已知关于x的一元二次方程x2+bx﹣c=0无实数解,则抛物线y=﹣x2﹣bx+c经过 象限.
14.(4分)如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是 .
15.(4分)将抛物线y1=x2﹣2x﹣3先向左平移1个单位,再向上平移4个单位后,与抛物线y2=ax2+bx+c重合,现有一直线y3=2x+3与抛物线y2=ax2+bx+c相交.当y2≤y3时自变量x的取值范围是 .
16.(4分)如图所示,在△ABD中,BC为AD边上的高线,tan∠BAD=1,在BC上截取CG=CD,连结AG,将△ACG绕点C旋转,使点G落在BD边上的F处,A落在E处,连结BE,若AD=4,tanD=3,则△CFD和△ECF的面积比为 ;BE长为 .
三、解答题:本题有7小题,共66分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)Jack同学寒假去野生动物园游玩,从Baidu地图查找线路发现,几条线路均要换乘,乘车方案如下:在出发站点可选择空调车A,空调车B,普通车a;换乘点可选择空调车C,普通车b,普通车c,所有车辆均在同一站点换乘.
(1)求Jack同学在出发点乘坐空调车的概率;
(2)已知空调车票价2元,普通车票价1元,请用树状图或列表法求Jack同学到达动物园恰好花费3元公交费的概率.
18.(8分)Jack同学从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=,然后又沿着坡比i=1:3的斜坡向上走了500米到达点C.
(1)Jack从点A到点B上升的高度是多少米?
(2)Jack从点A到点C上升的高度CD是多少米?
19.(8分)如图1所示,点P是线段AB的中点,且AB=12,现分别以AP,BP为边,在AB的同侧作等边△MAP和△NBP,连结MN.
(1)请只用不含刻度的直尺在图1中找到△MNP外接圆的圆心O,并保留作图痕迹;
(2)若将“点P是线段AB的中点”改成“点P是线段AB上异于端点的任意一点”,其余条件不变(如图2),请用文字写出△MNP外接圆圆心O的位置,并求出该圆半径的最小值.
20.(10分)如图窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形,现在制作一个窗户边框的材料总长度为6米.( π取3)
(1)若设扇形半径为x,请用含x的代数式表示出AB.并求出x的取值范围.
(2)当x为何值时,窗户透光面积最大,最大面积为多少?(窗框厚度不予考虑)
21.(10分)在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
22.(12分)现有一次函数y=mx+n和二次函数y=mx2+nx+1,其中m≠0,
(1)若二次函数y=mx2+nx+1经过点(2,0),(3,1),试分别求出两个函数的解析式.
(2)若一次函数y=mx+n经过点(2,0),且图象经过第一、三象限.二次函数y=mx2+nx+1经过点(a,y1)和(a+1,y2),且y1>y2,请求出a的取值范围.
(3)若二次函数y=mx2+nx+1的顶点坐标为A(h,k)(h≠0),同时二次函数y=x2+x+1也经过A点,已知﹣1<h<1,请求出m的取值范围.
23.(12分)如图所示,△ABC为Rt△,∠ACB=90°,点D为AB的中点,点E为边AC上的点,连结DE,过点E作EF⊥ED交BC于F,以DE,EF为邻边作矩形DEFG,已知AC=8.
(1)如图1所示,当BC=6,点G在边AB上时,求DE的长.
(2)如图2所示,若,点G在边BC上时,求BC的长.
(3)①若,且点G恰好落在Rt△ABC的边上,求BC的长.
②若(n为正整数),且点G恰好落在Rt△ABC的边上,请直接写出BC的长.
2018-2019学年浙江省杭州市萧山区城厢片九年级(下)期初数学试卷
参考答案与试题解析
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项最符合题目要求.
1.【解答】解:A、旭日东升是必然事件,正确;
B、守株待兔是随机事件,不符合题意;
C、大海捞针是不可能事件,不符合题意;
D、明天放假是随机事件,不符合题意;
故选:A.
2.【解答】解:二次函数y=(x+1)2图象与x轴交点横坐标就是(x+1)2=0的根,
解方程(x+1)2=0,
得:x1=x2=﹣1,
∴二次函数y=(x+1)2图象与x轴交点坐标为(﹣1,0);
故选:A.
3.【解答】
解:在Rt△ACB中,BC=m,∠A=α,
∴sinA=,
∴AB==,
故选:C.
4.【解答】解:∵点P到点O的距离为8,圆O的半径为10,
∴8<10,
∴点P在圆内,
∴过点P的直线l与圆O的位置关系为相交,
故选:A.
5.【解答】解:设圆心角为n°.
由题意:=π,
∴n=60,
故选:C.
6.【解答】解:如图,连接OE,
∵DC=DO,
∴∠DOC=∠C=18°,
∴∠ODE=∠DOC+∠C=36°,
∵OD=OE,
∴∠OED=∠ODE=36°,
∴∠EOB=∠C+∠OED=18°+36°=54°,
∴∠EAB=∠EOB=27°,
故选:C.
7.【解答】解:∵AD∥BC,
∴△AOD∽△COB,
∴=()2,
∵=,
∴=()2,
∴S22=S1?S3,
即S2是S1和S3的比例中项.
故选:A.
8.【解答】解:①将点(1,y1)代入二次函数y=ax2+bx+c,
得到y1=a+b+c,
∵y1>0,
∴a+b+c>0.
故①正确.
②若a=2b时,函数对称轴x=﹣=﹣,
当a>0时,y1<y2,
当a<0时,y1>y2.
故②错误.
③∵a+b<0,
∴a<﹣b
当a<0时,﹣<,此时只能y1>0,y2<0;
当a>0时,﹣>,此时只能y1<0,y2>0;
所以y1<0,y2>0,且a+b<0时,a>0.
故③正确.
故选:C.
9.【解答】解:A、由一次函数图象可知,k>0,∴﹣k<0,∴二次函数的图象开口应该向下,故A选项不合题意;
B、由一次函数图象可知,k>0,∴﹣k<0,,∴二次函数的图象开口向下,且对称轴在x轴的正半轴,故B选项不合题意;
C、由一次函数图象可知,k<0,∴﹣k>0,,∴二次函数的图象开口向上,且对称轴在x轴的负半轴,一次函数必经过点(2,0),当x=2时,二次函数值y=﹣4k>0,故C选项符合题意;
D、由一次函数图象可知,k<0,∴﹣k>0,,∴二次函数的图象开口向上,且对称轴在x轴的负半轴,一次函数必经过点(2,0),当x=2时,二次函数值y=﹣4k>0,故D选项不合题意;
故选:C.
10.【解答】解:①如图1中,
∵DP≥1,当△APB为等腰三角形,
∴只有AP=AB,
在Rt△ADP中,∵∠D=90°,AP=2,AD=1,
∴PA=2AD,
∴∠APD=30°,
∵CD∥AB,
∴∠CPB=∠ABP,
∵AP=AB,
∴∠ABP=∠APB,
∴∠APB=∠CPB=75°,
∵P,Q关于BC对称,
∴BP=BQ,
∴∠BPC=∠BQC=75°,
∴△APB∽△BPQ,故①正确.
②如图2中,作△APQ的外接圆⊙O.
当点O与B重合时,⊙O的半径最小,此时⊙O的面积为4π,
当点P与C重合时,设OA=OP=x,
在Rt△AOB中,则有x2=22+(x﹣1)2,
∴x=,
此时⊙O的面积=π,
观察图象可知:4π≤S<.故②正确,
故选:A.
二、填空题:本题有6个小题,每小题4分,共24分.
11.【解答】解:∵cos30°=,
∴cos30°>.
故答案为:>.
12.【解答】解:设取走x个黑球,则放入x个黄球,
由题意,得≥,
解得:x≥,
∵x为整数,
∴x的最小正整数解是x=9.
答:至少取走了9个黑球.
故答案为:9.
13.【解答】解:∵关于x的一元二次方程x2+bx﹣c=0无实数解,
∴△=b2+4c<0,
∵抛物线y=﹣x2﹣bx+c中,二次项系数﹣1<0,
∴抛物线的开口向下,
∵判别式=(﹣b)2﹣4×(﹣1)×c=b2+4c<0,
∴抛物线与x轴无交点,
∴抛物线在x轴的下方,
∴抛物线y=﹣x2﹣bx+c经过第三、四象限;
故答案为:三、四.
14.【解答】解:
当O、Q、P三点一线且OP⊥BC时,PQ有最小值,设AC与圆的切点为D,连接OD,如图,
∵AC为圆的切线,
∴OD⊥AC,
∵AC=8,BC=6,AB=10,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴OD∥BC,且O为AB中点,
∴OD为△ABC的中位线,
∴OD=BC=3,
同理可得PO=AC=4,
∴PQ=OP﹣OQ=4﹣3=1,
故答案为:1.
15.【解答】解:y1=x2﹣2x﹣3=(x﹣1)2﹣4,
把y1=(x﹣1)2﹣4先向左平移1个单位,再向上平移4个单位后所得抛物线解析式为y=x2,
解方程组得或,
所以直线y3=2x+3与抛物线y2=ax2+bx+c交点坐标为(﹣1,1),(3,9),
当﹣1≤x≤3时,y2≤y3.
故答案为﹣1≤x≤3.
16.【解答】解:作CM⊥DF于M,如图所示:
则∠CMD=90°,
∵在△ABD中,BC为AD边上的高线,tan∠BAD=1,
∴∠BCD=∠ACB=90°,AC=BC,
在Rt△BCD中,∵tanD=3=,
∴BC=3CD,
∵AD=AC+CD=BC+CD=4,
∴CD=1,AC=BC=3,
∵∠CMD=∠BCD,∠D=∠D,
∴△CDM∽△BDC,==,
∴=,
在△AGC和△BDC中,,
∴△AGC≌△BDC(SAS),
∴∠CAG=∠CBD,△AGC的面积=△BDC的面积,∠CAG=∠CBD,
由旋转的性质得:CF=CD,EC=AC=BC,∠CEF=∠CAG,∠BCF=∠ACN,
∴△CDF的面积=2△CDM的面积,
∴△CFD的面积:△ECF的面积=1:5;
∵CG=CD,
∴CG=CF,
在△ACN和△BCF中,,
∴△ACN≌△BCF(ASA),
∴AN=BF,CN=CF=CD=CG=1,
∴GN=DF,BC:CG=CE:CN,
∵∠GCN=∠BCE,
∴△CGN∽△CBE,
∴=,
在Rt△DCM中,tanD=3,CD=1,
∴DM=,
∵CD=CF,CM⊥DF,
∴DF=2DM=,
∴GN=,
∴=,
解得:BE=;
故答案为:1:5,.
三、解答题:本题有7小题,共66分.解答应写出文字说明、证明过程或演算步骤.
17.【解答】解:(1)∵在出发站点可选择空调车A、空调车B、普通车a,
∴Jack在出发站点乘坐空调车的概率为:;
(2)如图所示:
,
一共有9种组合,只有Ab,Ac,Bb,Bc,aC组合恰好花费3元,
故Jack到达动物园恰好花费3元公交费的概率为:.
18.【解答】解:(1)作BF⊥AD
在Rt△ABF中,BF=AB×sinα=650×=200(米),
答:Jack从点A到点B上升的高度是200米;
(2)作BE⊥CD
在Rt△CBE中,CE:BE=1:3,
可得CE:BC=1:,
可得CE=,
得CD=(200+50)m,
答:Jack从点A到点C上升的高度CD是(200+50)米.
19.【解答】解:(1)如图,连接AN,BM交于点O,点O即为所求.
(2)O点为∠MAB角平分线和∠NBA角平分线的交点.
当OP⊥AB时,半径最短,
可得r=.
20.【解答】解:(1)根据题意得:2AB+7x+πx=2AB+10x=6,
整理得:AB=3﹣5x;
根据3﹣5x>0,
所以x的取值范围是:0<x<;
(2)设面积为S,则S=2x(3﹣5x)+x2=﹣x2+6x=﹣(x﹣)2+,
当x=时,S最大=.
21.【解答】(1)证明:连接OE.
∵OE=OB,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBC,
∴∠EBC=∠OEB,
∴OE∥BC,
∴∠OEA=∠C,
∵∠ACB=90°,
∴∠OEA=90°
∴AC是⊙O的切线;
(2)解:连接OE、OF,过点O作OH⊥BF交BF于H,
由题意可知四边形OECH为矩形,
∴OH=CE,
∵BF=6,
∴BH=3,
在Rt△BHO中,OB=5,
∴OH==4,
∴CE=4.
22.【解答】解:(1)将点(2,0),(3,1),代入一次函数y=mx+n中,
,
解得,
∴一次函数的解析式是y=x﹣2,
再将点(2,0),(3,1),代入二次函数y=mx2+nx+1,
,
解得,
∴二次函数的解析式是y═x2++1.
(2)∵一次函数y=mx+n经过点(2,0),
∴n=﹣2m,
∵二次函数y=mx2+nx+1的对称轴是x=﹣,
∴对称轴为x=1,
又∵一次函数y=mx+n图象经过第一、三象限,
∴m>0,
∵y1>y2,
∴1﹣a>1+a﹣1,
∴a<.
(3)∵y=mx2+nx+1的顶点坐标为A(h,k),
∴k=mh2+nh+1,且h=﹣,
又∵二次函数y=x2+x+1也经过A点,
∴k=h2+h+1,
∴mh2+nh+1=h2+h+1,
∴,
又∵﹣1<h<1,
∴m<﹣2或m>0.
23.【解答】解:(1)如图1中,
在Rt△ABC中,∵AC=8,BC=6,
∴AB===10,
∵D是AB中点,
∴AD=DB=5,
∵∠A=∠A,
∴tan∠A==,
∴=,
∴DE=.
(2)如图2中,设DE=x,则EF=EC=2x.
∵DE∥BC,AD=DB,
∴AE=EC=2x,
∴4x=8,
∴x=2,
∴DE=BC,
∴BC=2DE=4.
(3)①当点G落在BC边上时,如图2中,设DE=x,则EF=EC=4x,
可得:AE=EC=4x,8x=8,
∴x=1,
∴BC=2DE=2.
当点G落在AB边上时,
作DH⊥AC于H,设DH=x,则CE=4x,BC=2x,EH=4﹣4x,
利用△HDE∽△CAB,可得,解得x=,则BC=.
②若(n为正整数)时,同法可知:BC=或.
同课章节目录
