2018-2019学年北京四中九年级(下)开学数学试卷含答案
文档属性
| 名称 | 2018-2019学年北京四中九年级(下)开学数学试卷含答案 | 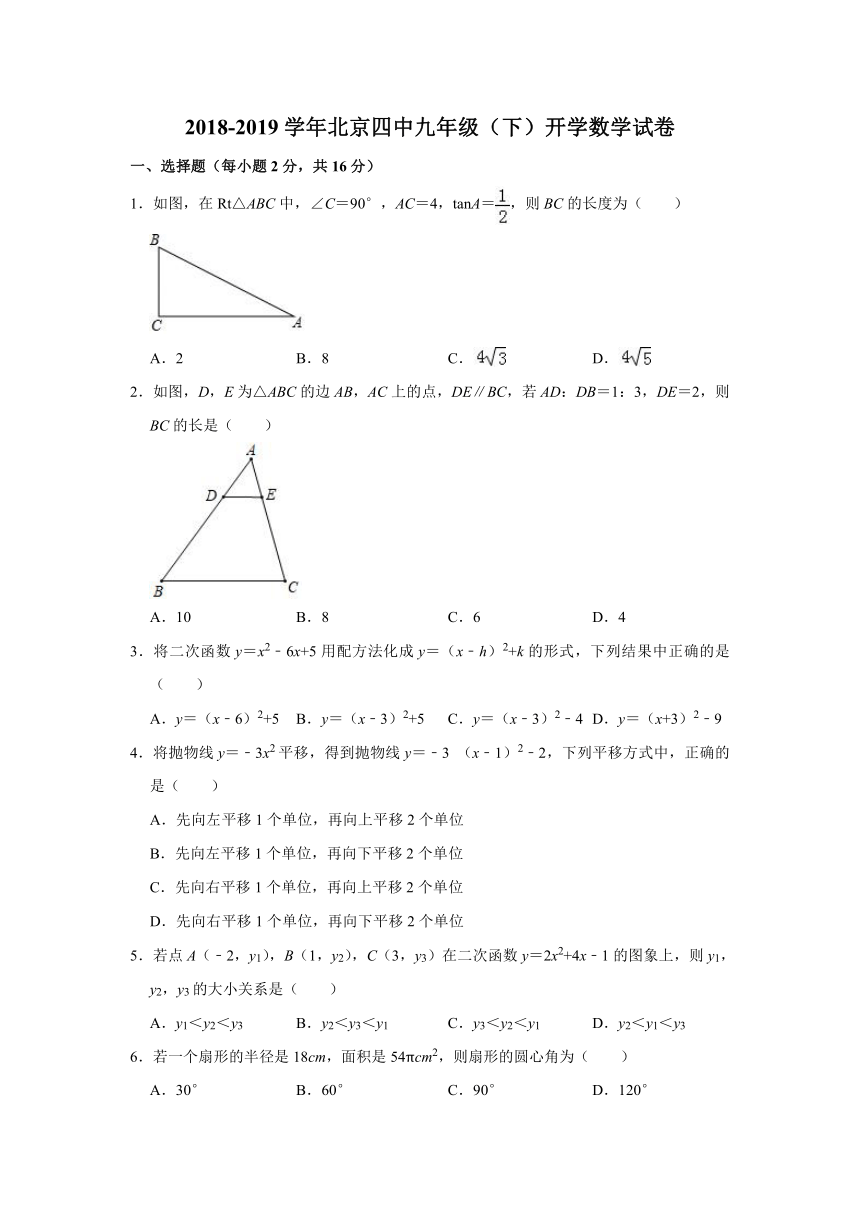 | |
| 格式 | zip | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-01 20:29:24 | ||
图片预览



文档简介
2018-2019学年北京四中九年级(下)开学数学试卷
一、选择题(每小题2分,共16分)
1.如图,在Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长度为( )
A.2 B.8 C. D.
2.如图,D,E为△ABC的边AB,AC上的点,DE∥BC,若AD:DB=1:3,DE=2,则BC的长是( )
A.10 B.8 C.6 D.4
3.将二次函数y=x2﹣6x+5用配方法化成y=(x﹣h)2+k的形式,下列结果中正确的是( )
A.y=(x﹣6)2+5 B.y=(x﹣3)2+5 C.y=(x﹣3)2﹣4 D.y=(x+3)2﹣9
4.将抛物线y=﹣3x2平移,得到抛物线y=﹣3 (x﹣1)2﹣2,下列平移方式中,正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
5.若点A(﹣2,y1),B(1,y2),C(3,y3)在二次函数y=2x2+4x﹣1的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y2<y1<y3
6.若一个扇形的半径是18cm,面积是54πcm2,则扇形的圆心角为( )
A.30° B.60° C.90° D.120°
7.如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,若∠A=30°,AB=2,则AC等于( )
A.4 B.6 C. D.
8.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x
…
﹣1
0
1
3
…
y
…
﹣1
3
5
3
…
下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题2分,共16分)
9.若二次函数y=x2+2x+2k﹣4的图象与x轴有两个交点,则k的取值范围为 .
10.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC= .
11.请写出一个开口向下,且经过点(﹣1,0)的二次函数的解析式 .
12.如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为 .
13.如图,四边形ABCD是⊙O内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD的度数为 .
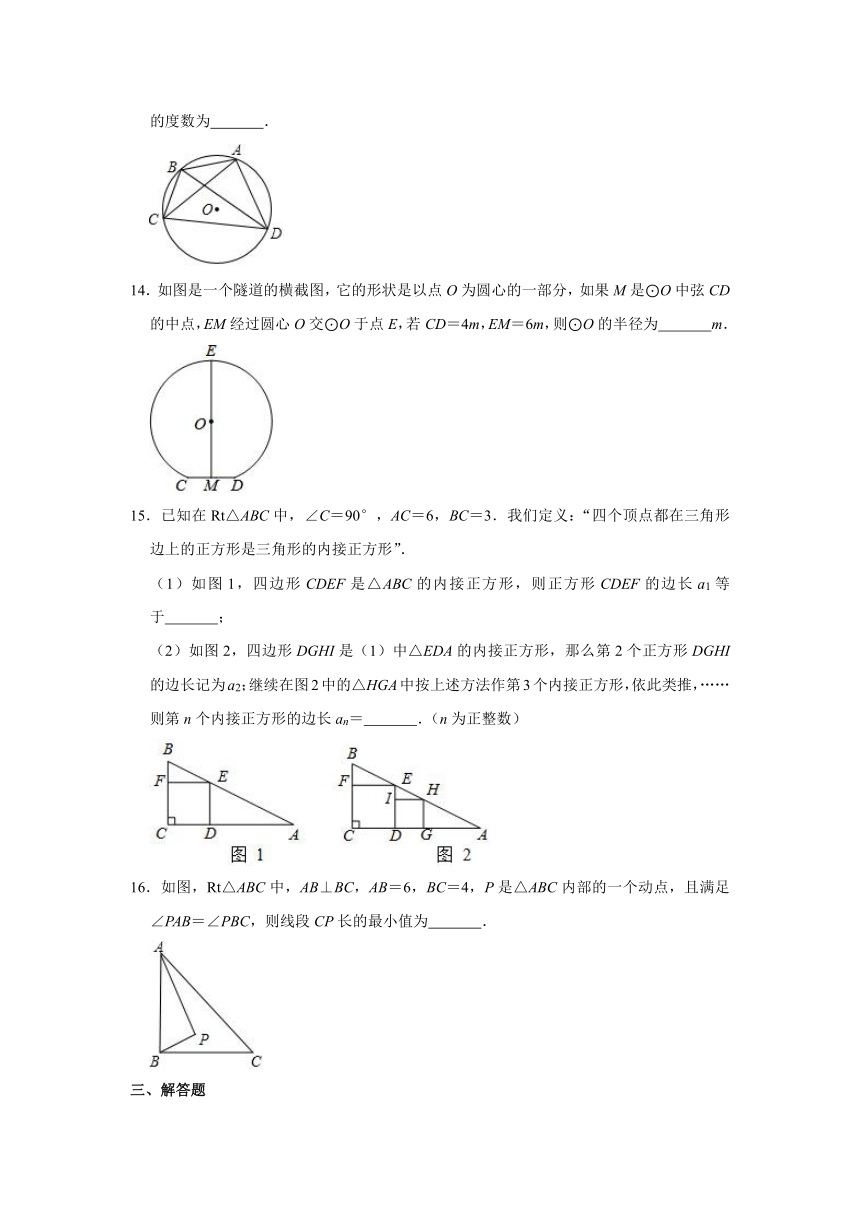
14.如图是一个隧道的横截图,它的形状是以点O为圆心的一部分,如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,若CD=4m,EM=6m,则⊙O的半径为 m.
15.已知在Rt△ABC中,∠C=90°,AC=6,BC=3.我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.
(1)如图1,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1等于 ;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形,依此类推,……则第n个内接正方形的边长an= .(n为正整数)
16.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 .
三、解答题
17.(5分)在数学课上,老师提出利用尺规作图完成下面问题:
已知:△ABC是⊙O的内接三角形.求作:△ABC中∠BAC的平分线.
小明的作法如下:
(1)作BC边的垂直平分线DE,交BC于点D,交弧BC于点E;
(2)连接AE,交BC边于点F;则线段AF为所求△ABC中∠BAC的平分线.
根据小明设计的尺规作图过程,
(1)在图中补全图形(尺规作图,保留作图痕迹);
(2)完成下面的证明.
证明:∵OB=OC,DE是线段BC的垂直平分线
∴圆心O在直线DE上( ).
∵DE⊥BC,
∴=( ).
∴∠BAE=∠CAE( ),
∴线段AF为所求△ABC中∠BAC的平分线.
18.(5分)计算:tan60°﹣sin245°+tan45°﹣2cos30°.
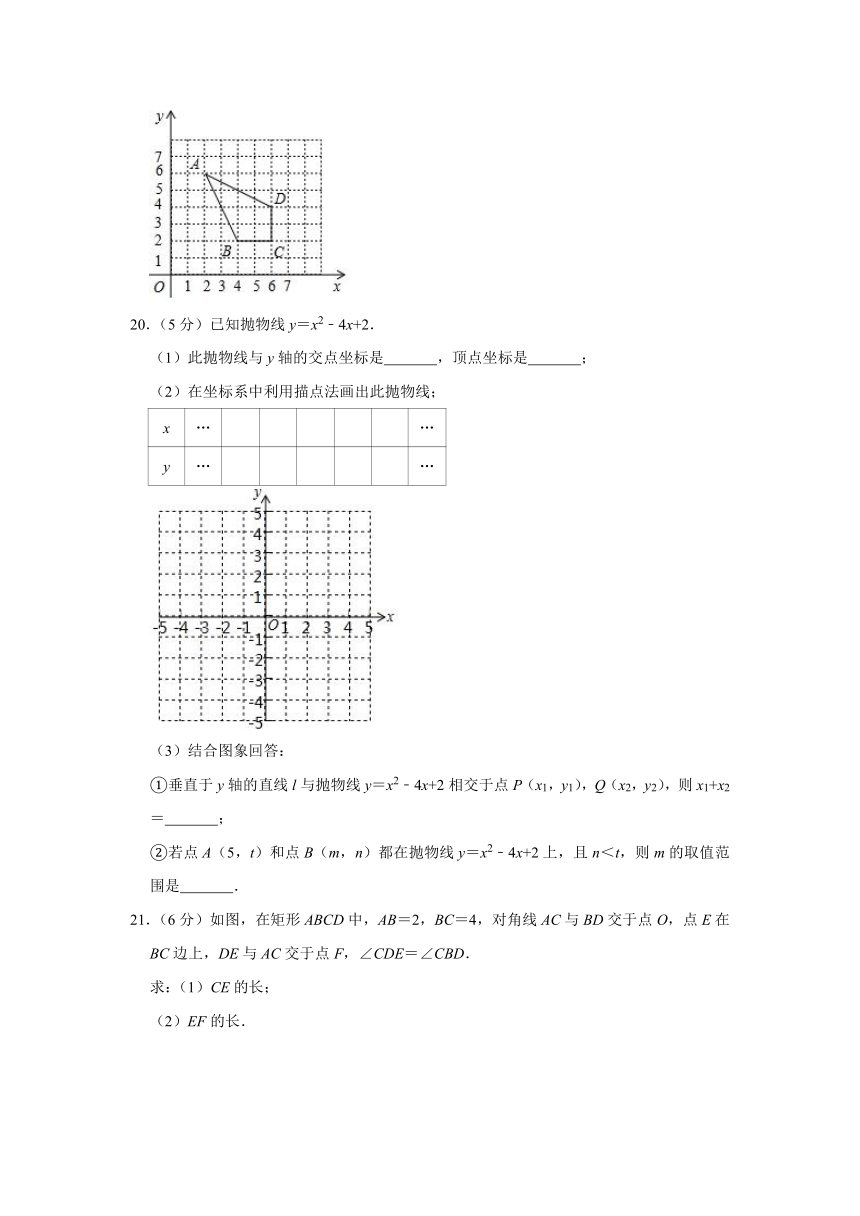
19.(5分)如图,四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4).
(1)在第一象限内,以原点O为位似中心,画出四边形ABCD的位似图形A1B1C1D1,使对应边长变为原来的;
(2)将线段AB绕点B顺时针旋转90°得到线段A2B,画出线段A2B,并计算点A所经过的路径长.
20.(5分)已知抛物线y=x2﹣4x+2.
(1)此抛物线与y轴的交点坐标是 ,顶点坐标是 ;
(2)在坐标系中利用描点法画出此抛物线;
x
…
…
y
…
…
(3)结合图象回答:
①垂直于y轴的直线l与抛物线y=x2﹣4x+2相交于点P(x1,y1),Q(x2,y2),则x1+x2= ;
②若点A(5,t)和点B(m,n)都在抛物线y=x2﹣4x+2上,且n<t,则m的取值范围是 .
21.(6分)如图,在矩形ABCD中,AB=2,BC=4,对角线AC与BD交于点O,点E在BC边上,DE与AC交于点F,∠CDE=∠CBD.
求:(1)CE的长;
(2)EF的长.
22.(5分)已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
23.(5分)如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF.
(1)求证:四边形BDCF为菱形;
(2)若CE=4,AC=6,求四边形BDCF的面积.
24.(6分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:∠CBF=∠CAB;
(2)连接BD,AE交于点H,若AB=5,tan∠CBF=,求BH的值.
25.(6分)如图,半圆O的直径AB=5cm,点M在AB上且AM=1cm,点P是半圆O上的动点,过点B作BQ⊥PM交PM(或PM的延长线)于点Q.设PM=xcm,BQ=ycm.(当点P与点A或点B重合时,y的值为0)
小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小石的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm
1
1.5
2
2.5
3
3.5
4
y/cm
0
3.7
3.8
3.3
2.5
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:
当BQ与直径AB所夹的锐角为60°时,PM的长度约为 cm.
26.(6分)已知抛物线y=ax2+bx+c经过点A(0,3)和B(4,3).
(1)直接写出a,b之间的数量关系式: ;
(2)若抛物线的顶点在x轴上,求a的值;
(3)若M(﹣1,0),N(3,0),且抛物线与线段MN只有一个公共点,求a的取值范围.
27.(7分)如图1,在等腰直角△ABC中,∠ACB=90°,P是射线CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得CQ=CP,过点作QH⊥AP于点H,交直线AB于点M.
①在图1中补全图形
②若∠PAC=α,用含α的式子表示∠AMQ的大小为∠AMQ= ;
③探究线段MB与PQ之间的数量关系,并给出证明.
28.(7分)在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(,0),T(1,)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣x+2与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
2018-2019学年北京四中九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(每小题2分,共16分)
1.【解答】解:∵在Rt△ABC中,∠C=90°,AC=4,
∴tanA===,
∴BC=2.
故选:A.
2.【解答】解:∵AD∥BC,
∴△ADE∽△ABC,
∴=,
即=,
∴BC=8.
故选:B.
3.【解答】解:y=x2﹣6x+5=x2﹣6x+9﹣4=(x﹣3)2﹣4,
故选:C.
4.【解答】解:∵y=﹣3x2的顶点坐标为(0,0),y=﹣3(x﹣1)2﹣2的顶点坐标为(1,﹣2),
∴将抛物线y=﹣3x2向右平移1个单位,再向下平移2个单位,可得到抛物线y=﹣3(x﹣1)2﹣2.
故选:D.
5.【解答】解:对称轴为直线x=﹣=﹣1,
∵a=2>0,
∴x<﹣1时,y随x的增大而减小,
x>﹣1时,y随x的增大而增大,
∵点A(﹣2,y1)的对称点为(0,y1),
∴y1<y2<y3.
故选:A.
6.【解答】解:设扇形的圆心角为n,
则=54π,
解得,n=60°,
故选:B.
7.【解答】解:连接OB.
∵AB是⊙O的切线,B为切点,
∴OB⊥AB,
在直角△OAB中,OB=AB?tanA=2×=2,
则OA=2OB=4,
∴AC=4+2=6.
故选:B.
8.【解答】解:(1)由图表中数据可得出:x=1时,y=5,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故(1)正确;
(2)∵二次函数y=ax2+bx+c开口向下,且对称轴为x=1.5,∴当x≥1.5时,y的值随x值的增大而减小,故(2)错误;
(3)∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b﹣1)x+c=0的一个根,故(3)正确;
(4)∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2+(b﹣1)x+c>0,故(4)正确.
故选:C.
二、填空题(每小题2分,共16分)
9.【解答】解:根据题意知,△=22﹣4×1×(2k﹣4)>0,
解得:k<;
故答案为:k<.
10.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴=,
∵AB=CD,
∴DE:EC=2:3.
故答案为:2:3.
11.【解答】解:二次函数y=﹣x2+1开口向下,且经过(﹣1,0).
故答案为:y=﹣x2+1(答案不唯一).
12.【解答】解:∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,AB=2AC,PO⊥AB,
∴∠PAB=60°,
∴∠OAC=∠PAO﹣∠PAB=90°﹣60°=30°,
∴AO=2OC,
∵OC=1,
∴AO=2,
∴AC=,
∴AB=2AC=2,
∴△PAB的周长=6.
故答案为:6.
13.【解答】解:∵∠CBD=80°,
∴∠CAD=∠CBD=80°.
∵∠BAC=30°,
∴∠BAD=30°+80°=110°.
∵四边形ABCD是⊙O内接四边形,
∴∠BCD=180°﹣∠BAD=180°﹣110°=70°.
故答案为:70°.
14.【解答】解:∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
又CD=4则有:CM=CD=2,
设圆的半径是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
所以圆的半径长是.
故答案为:.
15.【解答】解:(1)四边形CDEF是正方形,
∴EF=FC,EF∥FC,
∴△BFE∽△BCA,
∴=,
∴=,
∴a1=2,
故答案是:2;
(2)如图(2)四边形DGHI是正方形,
∴IH=ID,IH∥AD,
∴△EIH∽△EDA,
∴=,
∴=,
∴a2=,
如图3中,由以上同样的方法可以求得正方形PGQS的边长为:=,
第4的个正方形的边长为:=,
…
第n个内接正方形的边长an=,
故答案为:=.
16.【解答】解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC==5,
∴PC=OC﹣OP=5﹣3=2.
∴PC最小值为2.
故答案为2.
三、解答题
17.【解答】解:(1)如图,
(2)证明:∵OB=OC,DE是线段BC的垂直平分线
∴圆心O在直线DE上(到线段两端点距离相等的点在线段的垂直平分线上).
∵DE⊥BC,
∴=(垂径定理).
∴∠BAE=∠CAE(圆周角定理),
∴线段AF为所求△ABC中∠BAC的平分线.
故答案为到线段两端点距离相等的点在线段的垂直平分线上;垂径定理;圆周角定理.
18.【解答】解:原式=﹣()2+1﹣2×
=﹣+1﹣
=.
19.【解答】解:(1)如图所示,四边形A1B1C1D1即为所求.
(2)如图所示,线段A2B即为所求,
∵A2B==2,∠ABA2=90°,
∴点A所经过的路径长为=π.
20.【解答】解:(1)对于抛物线y=x2﹣4x+2令x=0得到y=2,
∴与y轴交点的坐标为(0,2);
∵y=x2﹣4x+2=(x﹣2)2﹣2,
∴顶点坐标(2,﹣2),
故答案为:(0,2),(2,﹣2);
(2)利用描点法画出图象如图所示:
x
…
0
1
2
3
4
…
y
…
2
﹣1
﹣2
﹣1
2
…
.
(3)结合图象:
①垂直于y轴的直线l与抛物线y=x2﹣4x+2相交于点P(x1,y1),Q(x2,y2),则x1+x2=4;
②若点A(5,t)和点B(m,n)都在抛物线y=x2﹣4x+2上,且n<t,则m的取值范围是﹣1<m<5;
故答案为4;﹣1<m<5.
21.【解答】解:(1)∵四边形ABCD是矩形,AB=2,BC=4,
∴AD∥BC,CD=AB=2,
∴∠ADB=∠CBD,
∵∠EDC=∠ADB,
∴∠EDC=∠CBD,
∵∠ECD=∠DCB,
∴△CDE∽△CBD,
∴CE:CD=CD:CB,
∴CE:2=2:4,
解得:CE=1;
(2)∵AD∥BC,
∴△ADF∽△CEF,
∴DF:EF=AD:CE=4:1,
∴EF:DE=1:5,
∵∠DCB=90°,
∴DE==,
∴EF=.
22.【解答】解:(1)过点A作AH⊥PQ,垂足为点H.
∵斜坡AP的坡度为1:2.4,∴=,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26m. 解得k=2.
∴AH=10m.
答:坡顶A到地面PQ的距离为10m.
(2)延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x﹣14.
在Rt△ABC中,tan76°=,即≈4.0,
解得x=,即x≈19,
答:古塔BC的高度约为19米.
23.【解答】证明:(1)∵DE⊥BC,∠ACB=90°,
∴∠BED=∠ACB,
∴DF∥AC,
∵CF∥AB,
∴四边形ADFC是平行四边形,
∴AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,
∵BD∥CF,
∴四边形BDCF是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴DC=BD,
∴四边形BDCF是菱形;
(2)∵四边形BDCF是菱形
∴BC=2CE=8,BC⊥DF
∵四边形ADFC是平行四边形,
∴DF=AC=6
∴S菱形BDCF=×BC×DF=24
24.【解答】(1)证明:连接AE,
∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=∠CAB,
∵BF是⊙O的切线,
∴∠CBF=∠BAE,
∴∠CBF=∠CAB.
(2)解:∵tan∠CBF=tan∠EAB=,
∴=,
∵AB=5,AB2=BE2+AE2,
∴25=BE2+4BE2,
∴BE=,
∵∠BAE=∠CAE,∠EBD=∠CAE,
∴∠EBD=∠EAB,
∴tan∠EBD==,
∴EH=,
∴BH==.
25.【解答】解:(1)当x=2时,PM⊥AB,此时Q与M重合,BQ=BM=4,
当x=4时,点P与B重合,此时BQ=0.
故答案为4,0.
(2)函数图象如图所示:
(3)如图,
在Rt△BQM中,∵∠Q=90°,∠MBQ=60°,
∴∠BMQ=30°,
∴BQ=BM=2,
观察图象可知y=2时,对应的x的值为1.1或3.7.
故答案为1.1或3.7.
26.【解答】解:(1)将A(0,3)和B(4,3)代入y=ax2+bx+c中得:
,
∴4a+b=0,
故答案为:4a+b=0;
(2)∵抛物线y=ax2+bx+c经过点A(0,3)和B(4,3),
∴对称轴为直线x=2,
∵x=2时,y=4a+2b+c=b+3,
∴顶点坐标为(2,b+3),
∵抛物线的顶点在x轴上,
∴b+3=0,
∴b=﹣3,
∴a=;
(3)y=ax2﹣4ax+3,
当抛物线恰好经过点M时,将M(﹣1,0)代入得:a+4a+3=0,
解得a=﹣,
当抛物线恰好经过点N时,将N(3,0)代入得:9a﹣12a+3=0,
解得a=1,
∴抛物线与线段MN只有一个公共点时,a的取值范围是﹣≤a≤1.
27.【解答】解:①如图所示:
②∠AMQ=45°+α;理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°﹣α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°﹣∠AHM﹣∠PAB=45°+α;
故答案为:45°+α;
③PQ=MB;理由如下:
连接AQ,作ME⊥QB,如图所示:
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=45°+α=∠AMQ,
∴AP=AQ=QM,
在△APC和△QME中,
,
∴△APC≌△QME(AAS),
∴PC=ME,
∵△MEB是等腰直角三角形,
∴PQ=MB,
∴PQ=MB.
28.【解答】解:(1)当⊙O的半径为1时.
①点M(2,1)关于⊙O的反称点不存在;
N(,0)关于⊙O的反称点存在,反称点N′(,0);
T(1,)关于⊙O的反称点存在,反称点T′(0,0);
②∵OP≤2r=2,OP2≤4,设P(x,﹣x+2),
∴OP2=x2+(﹣x+2)2=2x2﹣4x+4≤4,
∴2x2﹣4x≤0,
x(x﹣2)≤0,
∴0≤x≤2.
当x=2时,P(2,0),P′(0,0)不符合题意;
当x=0时,P(0,2),P′(0,0)不符合题意;
∴0<x<2;
(2)∵直线y=﹣x+2与x轴、y轴分别交于点A,B,
∴A(6,0),B(0,2),
∴=,
∴∠OBA=60°,∠OAB=30°.
设C(x,0).
①当C在OA上时,作CH⊥AB于H,则CH≤CP≤2r=2,
所以AC≤4,
C点横坐标x≥2(当x=2时,C点坐标(2,0),H点的反称点H′(2,0)在圆的内部);
②当C在A点右侧时,AC最大值为2,
所以C点横坐标x≤8.
综上所述,圆心C的横坐标的取值范围是2≤x≤8.
一、选择题(每小题2分,共16分)
1.如图,在Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长度为( )
A.2 B.8 C. D.
2.如图,D,E为△ABC的边AB,AC上的点,DE∥BC,若AD:DB=1:3,DE=2,则BC的长是( )
A.10 B.8 C.6 D.4
3.将二次函数y=x2﹣6x+5用配方法化成y=(x﹣h)2+k的形式,下列结果中正确的是( )
A.y=(x﹣6)2+5 B.y=(x﹣3)2+5 C.y=(x﹣3)2﹣4 D.y=(x+3)2﹣9
4.将抛物线y=﹣3x2平移,得到抛物线y=﹣3 (x﹣1)2﹣2,下列平移方式中,正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
5.若点A(﹣2,y1),B(1,y2),C(3,y3)在二次函数y=2x2+4x﹣1的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y2<y1<y3
6.若一个扇形的半径是18cm,面积是54πcm2,则扇形的圆心角为( )
A.30° B.60° C.90° D.120°
7.如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,若∠A=30°,AB=2,则AC等于( )
A.4 B.6 C. D.
8.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x
…
﹣1
0
1
3
…
y
…
﹣1
3
5
3
…
下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题2分,共16分)
9.若二次函数y=x2+2x+2k﹣4的图象与x轴有两个交点,则k的取值范围为 .
10.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC= .
11.请写出一个开口向下,且经过点(﹣1,0)的二次函数的解析式 .
12.如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为 .
13.如图,四边形ABCD是⊙O内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD的度数为 .
14.如图是一个隧道的横截图,它的形状是以点O为圆心的一部分,如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,若CD=4m,EM=6m,则⊙O的半径为 m.
15.已知在Rt△ABC中,∠C=90°,AC=6,BC=3.我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.
(1)如图1,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1等于 ;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形,依此类推,……则第n个内接正方形的边长an= .(n为正整数)
16.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 .
三、解答题
17.(5分)在数学课上,老师提出利用尺规作图完成下面问题:
已知:△ABC是⊙O的内接三角形.求作:△ABC中∠BAC的平分线.
小明的作法如下:
(1)作BC边的垂直平分线DE,交BC于点D,交弧BC于点E;
(2)连接AE,交BC边于点F;则线段AF为所求△ABC中∠BAC的平分线.
根据小明设计的尺规作图过程,
(1)在图中补全图形(尺规作图,保留作图痕迹);
(2)完成下面的证明.
证明:∵OB=OC,DE是线段BC的垂直平分线
∴圆心O在直线DE上( ).
∵DE⊥BC,
∴=( ).
∴∠BAE=∠CAE( ),
∴线段AF为所求△ABC中∠BAC的平分线.
18.(5分)计算:tan60°﹣sin245°+tan45°﹣2cos30°.
19.(5分)如图,四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4).
(1)在第一象限内,以原点O为位似中心,画出四边形ABCD的位似图形A1B1C1D1,使对应边长变为原来的;
(2)将线段AB绕点B顺时针旋转90°得到线段A2B,画出线段A2B,并计算点A所经过的路径长.
20.(5分)已知抛物线y=x2﹣4x+2.
(1)此抛物线与y轴的交点坐标是 ,顶点坐标是 ;
(2)在坐标系中利用描点法画出此抛物线;
x
…
…
y
…
…
(3)结合图象回答:
①垂直于y轴的直线l与抛物线y=x2﹣4x+2相交于点P(x1,y1),Q(x2,y2),则x1+x2= ;
②若点A(5,t)和点B(m,n)都在抛物线y=x2﹣4x+2上,且n<t,则m的取值范围是 .
21.(6分)如图,在矩形ABCD中,AB=2,BC=4,对角线AC与BD交于点O,点E在BC边上,DE与AC交于点F,∠CDE=∠CBD.
求:(1)CE的长;
(2)EF的长.
22.(5分)已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
23.(5分)如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF.
(1)求证:四边形BDCF为菱形;
(2)若CE=4,AC=6,求四边形BDCF的面积.
24.(6分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:∠CBF=∠CAB;
(2)连接BD,AE交于点H,若AB=5,tan∠CBF=,求BH的值.
25.(6分)如图,半圆O的直径AB=5cm,点M在AB上且AM=1cm,点P是半圆O上的动点,过点B作BQ⊥PM交PM(或PM的延长线)于点Q.设PM=xcm,BQ=ycm.(当点P与点A或点B重合时,y的值为0)
小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小石的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm
1
1.5
2
2.5
3
3.5
4
y/cm
0
3.7
3.8
3.3
2.5
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:
当BQ与直径AB所夹的锐角为60°时,PM的长度约为 cm.
26.(6分)已知抛物线y=ax2+bx+c经过点A(0,3)和B(4,3).
(1)直接写出a,b之间的数量关系式: ;
(2)若抛物线的顶点在x轴上,求a的值;
(3)若M(﹣1,0),N(3,0),且抛物线与线段MN只有一个公共点,求a的取值范围.
27.(7分)如图1,在等腰直角△ABC中,∠ACB=90°,P是射线CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得CQ=CP,过点作QH⊥AP于点H,交直线AB于点M.
①在图1中补全图形
②若∠PAC=α,用含α的式子表示∠AMQ的大小为∠AMQ= ;
③探究线段MB与PQ之间的数量关系,并给出证明.
28.(7分)在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(,0),T(1,)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣x+2与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
2018-2019学年北京四中九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(每小题2分,共16分)
1.【解答】解:∵在Rt△ABC中,∠C=90°,AC=4,
∴tanA===,
∴BC=2.
故选:A.
2.【解答】解:∵AD∥BC,
∴△ADE∽△ABC,
∴=,
即=,
∴BC=8.
故选:B.
3.【解答】解:y=x2﹣6x+5=x2﹣6x+9﹣4=(x﹣3)2﹣4,
故选:C.
4.【解答】解:∵y=﹣3x2的顶点坐标为(0,0),y=﹣3(x﹣1)2﹣2的顶点坐标为(1,﹣2),
∴将抛物线y=﹣3x2向右平移1个单位,再向下平移2个单位,可得到抛物线y=﹣3(x﹣1)2﹣2.
故选:D.
5.【解答】解:对称轴为直线x=﹣=﹣1,
∵a=2>0,
∴x<﹣1时,y随x的增大而减小,
x>﹣1时,y随x的增大而增大,
∵点A(﹣2,y1)的对称点为(0,y1),
∴y1<y2<y3.
故选:A.
6.【解答】解:设扇形的圆心角为n,
则=54π,
解得,n=60°,
故选:B.
7.【解答】解:连接OB.
∵AB是⊙O的切线,B为切点,
∴OB⊥AB,
在直角△OAB中,OB=AB?tanA=2×=2,
则OA=2OB=4,
∴AC=4+2=6.
故选:B.
8.【解答】解:(1)由图表中数据可得出:x=1时,y=5,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故(1)正确;
(2)∵二次函数y=ax2+bx+c开口向下,且对称轴为x=1.5,∴当x≥1.5时,y的值随x值的增大而减小,故(2)错误;
(3)∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b﹣1)x+c=0的一个根,故(3)正确;
(4)∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2+(b﹣1)x+c>0,故(4)正确.
故选:C.
二、填空题(每小题2分,共16分)
9.【解答】解:根据题意知,△=22﹣4×1×(2k﹣4)>0,
解得:k<;
故答案为:k<.
10.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴=,
∵AB=CD,
∴DE:EC=2:3.
故答案为:2:3.
11.【解答】解:二次函数y=﹣x2+1开口向下,且经过(﹣1,0).
故答案为:y=﹣x2+1(答案不唯一).
12.【解答】解:∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,AB=2AC,PO⊥AB,
∴∠PAB=60°,
∴∠OAC=∠PAO﹣∠PAB=90°﹣60°=30°,
∴AO=2OC,
∵OC=1,
∴AO=2,
∴AC=,
∴AB=2AC=2,
∴△PAB的周长=6.
故答案为:6.
13.【解答】解:∵∠CBD=80°,
∴∠CAD=∠CBD=80°.
∵∠BAC=30°,
∴∠BAD=30°+80°=110°.
∵四边形ABCD是⊙O内接四边形,
∴∠BCD=180°﹣∠BAD=180°﹣110°=70°.
故答案为:70°.
14.【解答】解:∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
又CD=4则有:CM=CD=2,
设圆的半径是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
所以圆的半径长是.
故答案为:.
15.【解答】解:(1)四边形CDEF是正方形,
∴EF=FC,EF∥FC,
∴△BFE∽△BCA,
∴=,
∴=,
∴a1=2,
故答案是:2;
(2)如图(2)四边形DGHI是正方形,
∴IH=ID,IH∥AD,
∴△EIH∽△EDA,
∴=,
∴=,
∴a2=,
如图3中,由以上同样的方法可以求得正方形PGQS的边长为:=,
第4的个正方形的边长为:=,
…
第n个内接正方形的边长an=,
故答案为:=.
16.【解答】解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC==5,
∴PC=OC﹣OP=5﹣3=2.
∴PC最小值为2.
故答案为2.
三、解答题
17.【解答】解:(1)如图,
(2)证明:∵OB=OC,DE是线段BC的垂直平分线
∴圆心O在直线DE上(到线段两端点距离相等的点在线段的垂直平分线上).
∵DE⊥BC,
∴=(垂径定理).
∴∠BAE=∠CAE(圆周角定理),
∴线段AF为所求△ABC中∠BAC的平分线.
故答案为到线段两端点距离相等的点在线段的垂直平分线上;垂径定理;圆周角定理.
18.【解答】解:原式=﹣()2+1﹣2×
=﹣+1﹣
=.
19.【解答】解:(1)如图所示,四边形A1B1C1D1即为所求.
(2)如图所示,线段A2B即为所求,
∵A2B==2,∠ABA2=90°,
∴点A所经过的路径长为=π.
20.【解答】解:(1)对于抛物线y=x2﹣4x+2令x=0得到y=2,
∴与y轴交点的坐标为(0,2);
∵y=x2﹣4x+2=(x﹣2)2﹣2,
∴顶点坐标(2,﹣2),
故答案为:(0,2),(2,﹣2);
(2)利用描点法画出图象如图所示:
x
…
0
1
2
3
4
…
y
…
2
﹣1
﹣2
﹣1
2
…
.
(3)结合图象:
①垂直于y轴的直线l与抛物线y=x2﹣4x+2相交于点P(x1,y1),Q(x2,y2),则x1+x2=4;
②若点A(5,t)和点B(m,n)都在抛物线y=x2﹣4x+2上,且n<t,则m的取值范围是﹣1<m<5;
故答案为4;﹣1<m<5.
21.【解答】解:(1)∵四边形ABCD是矩形,AB=2,BC=4,
∴AD∥BC,CD=AB=2,
∴∠ADB=∠CBD,
∵∠EDC=∠ADB,
∴∠EDC=∠CBD,
∵∠ECD=∠DCB,
∴△CDE∽△CBD,
∴CE:CD=CD:CB,
∴CE:2=2:4,
解得:CE=1;
(2)∵AD∥BC,
∴△ADF∽△CEF,
∴DF:EF=AD:CE=4:1,
∴EF:DE=1:5,
∵∠DCB=90°,
∴DE==,
∴EF=.
22.【解答】解:(1)过点A作AH⊥PQ,垂足为点H.
∵斜坡AP的坡度为1:2.4,∴=,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26m. 解得k=2.
∴AH=10m.
答:坡顶A到地面PQ的距离为10m.
(2)延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x﹣14.
在Rt△ABC中,tan76°=,即≈4.0,
解得x=,即x≈19,
答:古塔BC的高度约为19米.
23.【解答】证明:(1)∵DE⊥BC,∠ACB=90°,
∴∠BED=∠ACB,
∴DF∥AC,
∵CF∥AB,
∴四边形ADFC是平行四边形,
∴AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,
∵BD∥CF,
∴四边形BDCF是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴DC=BD,
∴四边形BDCF是菱形;
(2)∵四边形BDCF是菱形
∴BC=2CE=8,BC⊥DF
∵四边形ADFC是平行四边形,
∴DF=AC=6
∴S菱形BDCF=×BC×DF=24
24.【解答】(1)证明:连接AE,
∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=∠CAB,
∵BF是⊙O的切线,
∴∠CBF=∠BAE,
∴∠CBF=∠CAB.
(2)解:∵tan∠CBF=tan∠EAB=,
∴=,
∵AB=5,AB2=BE2+AE2,
∴25=BE2+4BE2,
∴BE=,
∵∠BAE=∠CAE,∠EBD=∠CAE,
∴∠EBD=∠EAB,
∴tan∠EBD==,
∴EH=,
∴BH==.
25.【解答】解:(1)当x=2时,PM⊥AB,此时Q与M重合,BQ=BM=4,
当x=4时,点P与B重合,此时BQ=0.
故答案为4,0.
(2)函数图象如图所示:
(3)如图,
在Rt△BQM中,∵∠Q=90°,∠MBQ=60°,
∴∠BMQ=30°,
∴BQ=BM=2,
观察图象可知y=2时,对应的x的值为1.1或3.7.
故答案为1.1或3.7.
26.【解答】解:(1)将A(0,3)和B(4,3)代入y=ax2+bx+c中得:
,
∴4a+b=0,
故答案为:4a+b=0;
(2)∵抛物线y=ax2+bx+c经过点A(0,3)和B(4,3),
∴对称轴为直线x=2,
∵x=2时,y=4a+2b+c=b+3,
∴顶点坐标为(2,b+3),
∵抛物线的顶点在x轴上,
∴b+3=0,
∴b=﹣3,
∴a=;
(3)y=ax2﹣4ax+3,
当抛物线恰好经过点M时,将M(﹣1,0)代入得:a+4a+3=0,
解得a=﹣,
当抛物线恰好经过点N时,将N(3,0)代入得:9a﹣12a+3=0,
解得a=1,
∴抛物线与线段MN只有一个公共点时,a的取值范围是﹣≤a≤1.
27.【解答】解:①如图所示:
②∠AMQ=45°+α;理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°﹣α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°﹣∠AHM﹣∠PAB=45°+α;
故答案为:45°+α;
③PQ=MB;理由如下:
连接AQ,作ME⊥QB,如图所示:
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=45°+α=∠AMQ,
∴AP=AQ=QM,
在△APC和△QME中,
,
∴△APC≌△QME(AAS),
∴PC=ME,
∵△MEB是等腰直角三角形,
∴PQ=MB,
∴PQ=MB.
28.【解答】解:(1)当⊙O的半径为1时.
①点M(2,1)关于⊙O的反称点不存在;
N(,0)关于⊙O的反称点存在,反称点N′(,0);
T(1,)关于⊙O的反称点存在,反称点T′(0,0);
②∵OP≤2r=2,OP2≤4,设P(x,﹣x+2),
∴OP2=x2+(﹣x+2)2=2x2﹣4x+4≤4,
∴2x2﹣4x≤0,
x(x﹣2)≤0,
∴0≤x≤2.
当x=2时,P(2,0),P′(0,0)不符合题意;
当x=0时,P(0,2),P′(0,0)不符合题意;
∴0<x<2;
(2)∵直线y=﹣x+2与x轴、y轴分别交于点A,B,
∴A(6,0),B(0,2),
∴=,
∴∠OBA=60°,∠OAB=30°.
设C(x,0).
①当C在OA上时,作CH⊥AB于H,则CH≤CP≤2r=2,
所以AC≤4,
C点横坐标x≥2(当x=2时,C点坐标(2,0),H点的反称点H′(2,0)在圆的内部);
②当C在A点右侧时,AC最大值为2,
所以C点横坐标x≤8.
综上所述,圆心C的横坐标的取值范围是2≤x≤8.
同课章节目录
