高中数学新人教B版必修3课件:第二章统计2.2.1用样本的频率分布估计总体的分布(二)(42张PPT)
文档属性
| 名称 | 高中数学新人教B版必修3课件:第二章统计2.2.1用样本的频率分布估计总体的分布(二)(42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-02 00:00:00 | ||
图片预览








文档简介
课件42张PPT。2.2.1 用样本的频率分布估计总体的分布(二)第二章情境引入导学
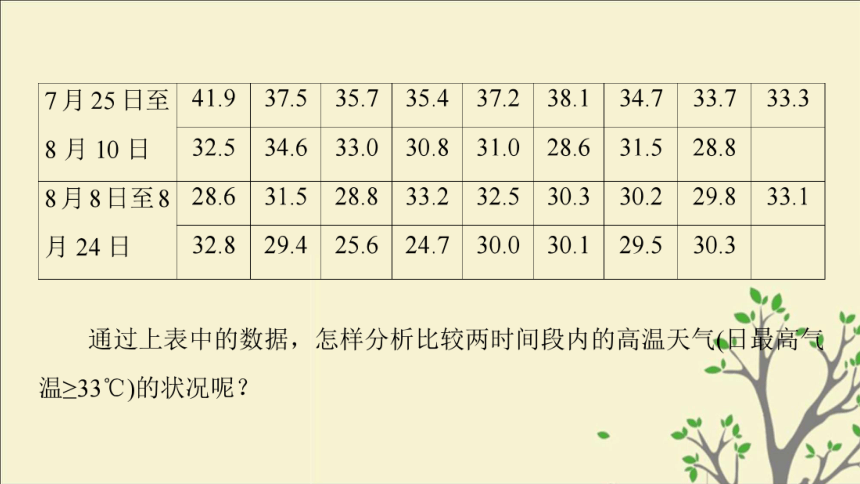
为了了解今年7月25日至8月24日某地区的气温分布状况,可以对这一地区往年这段时间的日最高气温进行抽样,并对得到的数据进行分析.我们随机抽取近年来这一地区7月25日至8月24日的日最高气温,得到如下两个样本(单位:℃):知识梳理
作频率分布直方图的步骤:
(1)求______.即一组数据中最大值与最小值的差.
(2)决定组数与组距.将数据分组时,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.这时应注意:①一般样本容量越大,所分组数越多;②为方便起见,组距的选择应力求“______”;③当样本容量不超过100时,按照数据的多少,通常分成5组~12组.极差取整(3)决定分点.
(4)列频率分布表.对落在各小组内数据的个数进行累计,这个累计数叫做各小组的频数,各个小组的频数除以__________,得各小组的频率
(5)绘制________________.以横轴表示样本分组,纵轴表示频率与组距的比值,以每个组距为底,以各频率除以组距的商为高,分别画成矩形,这样就得到了频率分布直方图.图中各个小长方形的面积等于相应各组的频率.样本容量频率分布直方图例1.抽查100袋洗衣粉,测得它们的重量如下(单位:g):
494 498 493 505 496 492 485 483 508 511 495 494 483 485 511 493 505 488 501 491 493 509 509 512 484 509 510 495 497 498 504 498 483 510 503 497 502 511 497 500 493 509 510 493 491 497 515 503 515 518 510 514 509 499 493 499 509 492 505 489 494 501 509 498 502 500 508 491 509 509 499 495 493 509 496 509 505 499 486 491 492 496 499 508 485 498 496 495
496 505 499 505 496 501 510 496 487 511 501 496
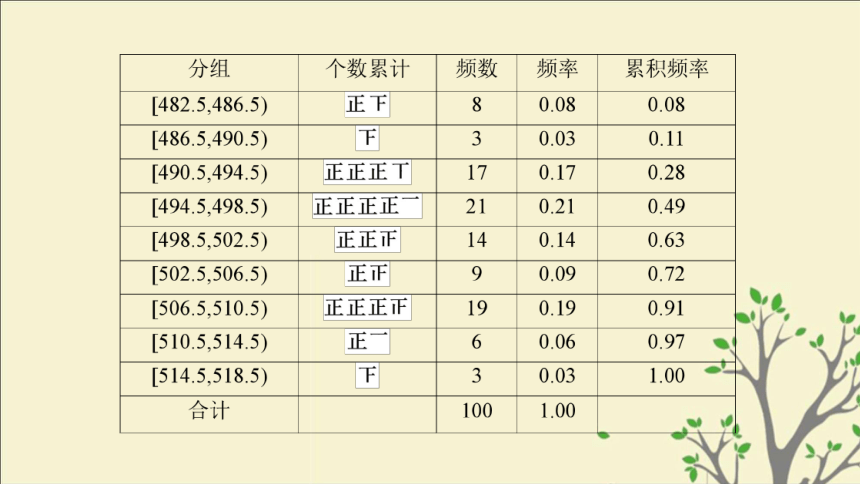
命题方向1 用样本频率分布估计总体分布 (1)列出样本的频率分布表;
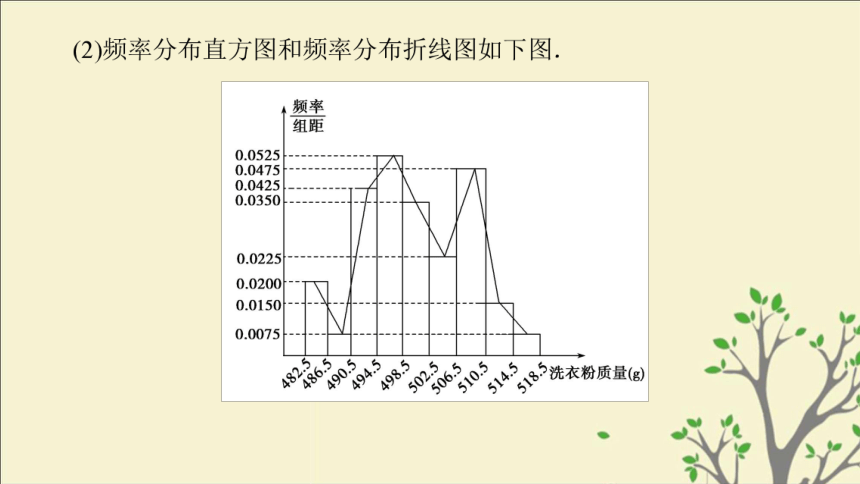
(2)画出频率分布直方图及频率分布折线图;
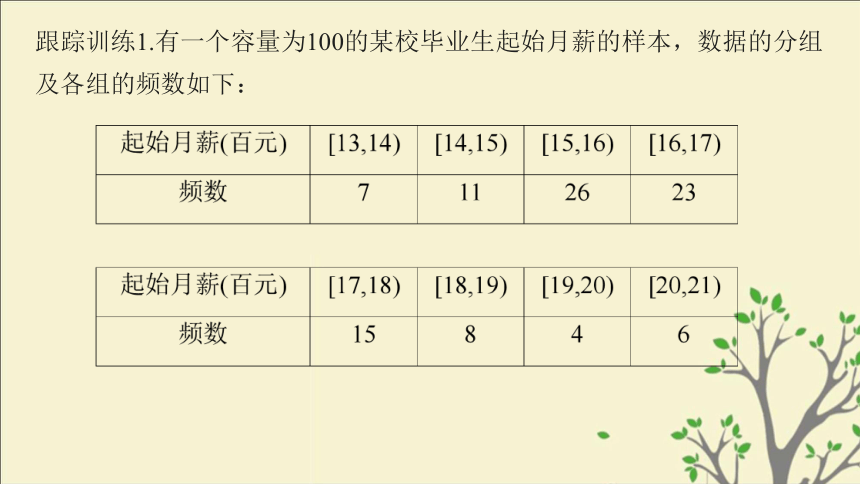
(3)估计质量在[494.5,506.5)g的频率以及质量不足500g的频率.解 (1)在样本数据中,最大值是518,最小值是483,它们相差35,若取组距为4g,则由于35÷4=8.75,要分9组,组数合适.于是决定取组距为4g分9组,使分点比数值多一位小数,且把第一组起点稍微减少一点,得分组如下:跟踪训练1.有一个容量为100的某校毕业生起始月薪的样本,数据的分组及各组的频数如下:(1)列出样本的频率分布表;
(2)画出频率分布直方图和频率分布折线图;
(3)根据频率分布估计该校毕业生起始月薪低于2 000元的频率.
解 (1)样本的频率分布表为:例2.有关部门从甲、乙两个城市所有的自动售货机中随机抽取了16台,记录下上午8?00~11?00之间各自的销售情况(单位:元):
甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41;
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23.
试用两种不同的方式分别表示上面的数据,并简要说明各自的优点.命题方向2 条形统计图及茎叶图的应用 解 从题目中的数据不易直接看出各自的分布情况,为此,我们将以上数据用条形统计图表示.
解法一:条形统计图如图所示解法二:茎叶图如图,两竖线中间的数字表示甲、乙销售额的十位数,两边的数字表示甲、乙销售额的个位数.
跟踪训练2.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60
C.120 D.140
【解析】根据频率分布直方图,200名学生中每周的自习时间不少于22.5小时的频率为(0.16+0.08+0.04)×2.5=0.7,故200名学生中每周的自习时间不少于22.5小时的人数为200×0.7=140.
【答案】D
例3.为了估计某人的射击技术状况,在他的训练记录中抽取了50次进行检验,他命中环数如下:
7 8 6 8 6 5 9 10 7 9 5 6 5 6 7 8 7 9 10 9
8 5 7 8 7 6 8 6 7 7 9 6 5 8 6 9 6 8 10 7
8 7 8 6 9 8 7 10 8 9
(1)作出频率分布表;
(2)画出频率分布条形图;
(3)估计该人命中6~8环的百分比是多少.命题方向3 频率分布表、频率分布直方图的应用 跟踪训练3.中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:酒后驾车和醉酒驾车,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是mg/100 mL).当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.据调查,某地区第一季度查处酒后驾车和醉酒驾车共2 880人.如图是对这2 880人的血酒含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数为( )
A.216
B.288
C.432
D.864
【解析】醉酒驾车的人数为(0.005+0.010)×10×2 880=432,故选C.
【答案】C
(4)列出频率分布表如下:A.0.01 B.0.02
C.0.03 D.0.04【解析】100名学生中体重在[56.5,64.5)的学生人数是(a+2×0.05+0.07)×2×100=40,解得a=0.03,故选C.
【答案】C当堂检测
1.为了了解学校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示,根据此图,估计该校2 000名高中男生中体重大于70.5 kg的人数为( )
【解析】2 000名男生中体重大于70.5 kg的人数大约为2 000×(0.04×2+0.035×2+0.015×2)=360(人).
【答案】B
A.300 B.360
C.400 D.450
【答案】C3.已知样本:10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11, 12,11.那么频
率为0.2的范围为( )
A.5.5~7.5 B.7.5~9.5
C.9.5~11.5 D.11.5~13.5【答案】D解 列出频率分布表如下:
从表中可以看出,频率为0.2的范围是11.5~13.5,故选D.4.某个容量为100的样本的频率分布直方图如下,则在区间[4,5)上的数据的频数为________.
【解析】本小题主要考查频率分布直方图.频数n=(1-0.05-0.10-0.15-0.40)×100=30.
【答案】30
解 (1)由用水量的频率分布直方图知,
该市居民该月用水量在区间(0.5,1],(1,1.5],(1.5,2],(2,2.5](2.5,3]内的频率依次为0.1,0.15,0.2,0.25,0.15.
所以该月用水量不超过3立方米的居民占85%,用水量不超过2立方米的居民占45%.依题意,w至少定为3.(1)如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.
为了了解今年7月25日至8月24日某地区的气温分布状况,可以对这一地区往年这段时间的日最高气温进行抽样,并对得到的数据进行分析.我们随机抽取近年来这一地区7月25日至8月24日的日最高气温,得到如下两个样本(单位:℃):知识梳理
作频率分布直方图的步骤:
(1)求______.即一组数据中最大值与最小值的差.
(2)决定组数与组距.将数据分组时,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.这时应注意:①一般样本容量越大,所分组数越多;②为方便起见,组距的选择应力求“______”;③当样本容量不超过100时,按照数据的多少,通常分成5组~12组.极差取整(3)决定分点.
(4)列频率分布表.对落在各小组内数据的个数进行累计,这个累计数叫做各小组的频数,各个小组的频数除以__________,得各小组的频率
(5)绘制________________.以横轴表示样本分组,纵轴表示频率与组距的比值,以每个组距为底,以各频率除以组距的商为高,分别画成矩形,这样就得到了频率分布直方图.图中各个小长方形的面积等于相应各组的频率.样本容量频率分布直方图例1.抽查100袋洗衣粉,测得它们的重量如下(单位:g):
494 498 493 505 496 492 485 483 508 511 495 494 483 485 511 493 505 488 501 491 493 509 509 512 484 509 510 495 497 498 504 498 483 510 503 497 502 511 497 500 493 509 510 493 491 497 515 503 515 518 510 514 509 499 493 499 509 492 505 489 494 501 509 498 502 500 508 491 509 509 499 495 493 509 496 509 505 499 486 491 492 496 499 508 485 498 496 495
496 505 499 505 496 501 510 496 487 511 501 496
命题方向1 用样本频率分布估计总体分布 (1)列出样本的频率分布表;
(2)画出频率分布直方图及频率分布折线图;
(3)估计质量在[494.5,506.5)g的频率以及质量不足500g的频率.解 (1)在样本数据中,最大值是518,最小值是483,它们相差35,若取组距为4g,则由于35÷4=8.75,要分9组,组数合适.于是决定取组距为4g分9组,使分点比数值多一位小数,且把第一组起点稍微减少一点,得分组如下:跟踪训练1.有一个容量为100的某校毕业生起始月薪的样本,数据的分组及各组的频数如下:(1)列出样本的频率分布表;
(2)画出频率分布直方图和频率分布折线图;
(3)根据频率分布估计该校毕业生起始月薪低于2 000元的频率.
解 (1)样本的频率分布表为:例2.有关部门从甲、乙两个城市所有的自动售货机中随机抽取了16台,记录下上午8?00~11?00之间各自的销售情况(单位:元):
甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41;
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23.
试用两种不同的方式分别表示上面的数据,并简要说明各自的优点.命题方向2 条形统计图及茎叶图的应用 解 从题目中的数据不易直接看出各自的分布情况,为此,我们将以上数据用条形统计图表示.
解法一:条形统计图如图所示解法二:茎叶图如图,两竖线中间的数字表示甲、乙销售额的十位数,两边的数字表示甲、乙销售额的个位数.
跟踪训练2.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60
C.120 D.140
【解析】根据频率分布直方图,200名学生中每周的自习时间不少于22.5小时的频率为(0.16+0.08+0.04)×2.5=0.7,故200名学生中每周的自习时间不少于22.5小时的人数为200×0.7=140.
【答案】D
例3.为了估计某人的射击技术状况,在他的训练记录中抽取了50次进行检验,他命中环数如下:
7 8 6 8 6 5 9 10 7 9 5 6 5 6 7 8 7 9 10 9
8 5 7 8 7 6 8 6 7 7 9 6 5 8 6 9 6 8 10 7
8 7 8 6 9 8 7 10 8 9
(1)作出频率分布表;
(2)画出频率分布条形图;
(3)估计该人命中6~8环的百分比是多少.命题方向3 频率分布表、频率分布直方图的应用 跟踪训练3.中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:酒后驾车和醉酒驾车,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是mg/100 mL).当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.据调查,某地区第一季度查处酒后驾车和醉酒驾车共2 880人.如图是对这2 880人的血酒含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数为( )
A.216
B.288
C.432
D.864
【解析】醉酒驾车的人数为(0.005+0.010)×10×2 880=432,故选C.
【答案】C
(4)列出频率分布表如下:A.0.01 B.0.02
C.0.03 D.0.04【解析】100名学生中体重在[56.5,64.5)的学生人数是(a+2×0.05+0.07)×2×100=40,解得a=0.03,故选C.
【答案】C当堂检测
1.为了了解学校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示,根据此图,估计该校2 000名高中男生中体重大于70.5 kg的人数为( )
【解析】2 000名男生中体重大于70.5 kg的人数大约为2 000×(0.04×2+0.035×2+0.015×2)=360(人).
【答案】B
A.300 B.360
C.400 D.450
【答案】C3.已知样本:10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11, 12,11.那么频
率为0.2的范围为( )
A.5.5~7.5 B.7.5~9.5
C.9.5~11.5 D.11.5~13.5【答案】D解 列出频率分布表如下:
从表中可以看出,频率为0.2的范围是11.5~13.5,故选D.4.某个容量为100的样本的频率分布直方图如下,则在区间[4,5)上的数据的频数为________.
【解析】本小题主要考查频率分布直方图.频数n=(1-0.05-0.10-0.15-0.40)×100=30.
【答案】30
解 (1)由用水量的频率分布直方图知,
该市居民该月用水量在区间(0.5,1],(1,1.5],(1.5,2],(2,2.5](2.5,3]内的频率依次为0.1,0.15,0.2,0.25,0.15.
所以该月用水量不超过3立方米的居民占85%,用水量不超过2立方米的居民占45%.依题意,w至少定为3.(1)如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.
