2018-2019学年湖南省彬州市贵阳市敖泉中学高一上学期期中考试数学试题
文档属性
| 名称 | 2018-2019学年湖南省彬州市贵阳市敖泉中学高一上学期期中考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 144.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-02 00:00:00 | ||
图片预览




文档简介
2018-2019学年湖南省彬州市贵阳市敖泉中学高一上学期期中考试数学试题
(本试卷150分,120分钟)
一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设全集,集合,,则( )
A. B. C. D.
2.已知集合,则下列式子表示正确的有( )
① ② ③ ④
A.1个 B.2个 C.3个 D.4个
3.函数的定义域为( )
A. B. C. D.
4.已知函数,则的值等于( )
A.4 B.2 C.1 D.0
5.已知幂函数y=f(x)的图象经过点(2,),则f(4)的值为( )
A. B.2 C. D.16
6.若函数在区间上是减函数,则实数的取值范围是( )
A. B. C. D.
7.计算:( )
A.2 B.6 C. 8 D. 12
8.已知函数f(x)=ax(a>0,a≠1)在[1,2]上的最大值和最小值的和为6,则a=( )
A.2 B.3 C.4 D.5
9.若a=log20.5,b=20.5,c=0.52,则a,b,c三个数的大小关系是( )
A.a<b<c B.b<c<a C.a<c<b D.c<a<b[
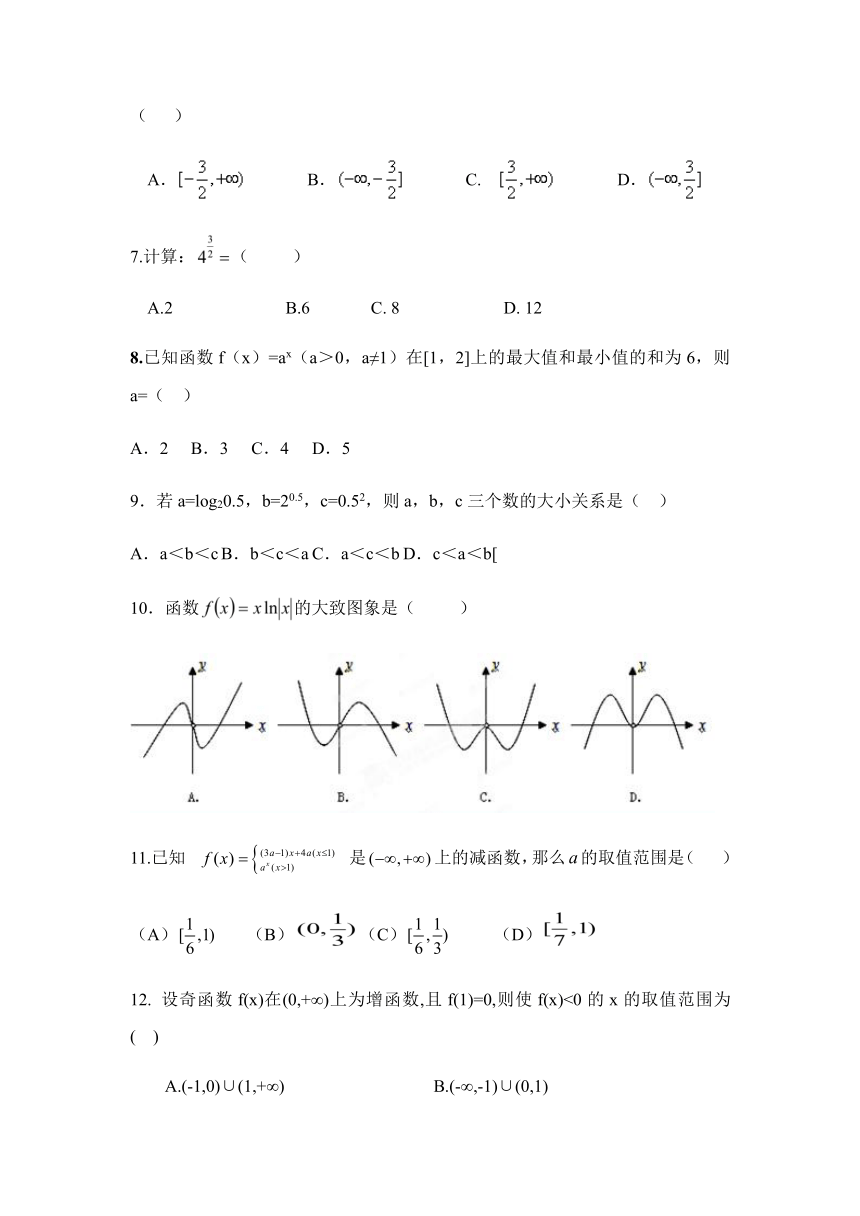
10.函数的大致图象是( )
11.已知 是上的减函数,那么的取值范围是( )
(A) (B)(C) (D)
12. 设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使f(x)<0的x的取值范围为 ( )
A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)
C.(-∞,-1)∪(1,+∞) D.(-1,0)∪(0,1)
宿州市汴北三校2017—2018学年度第一学期期中考试
高一数学答题卡
一选择题;(每题5分,共60分)
题号
1
2
3
4
5
6
答案
题号
7
8
9
10
11
12
答案
二.填空题(本大题共4小题,每小题5分,共20分,请把答案填在答题纸的横线上)
13.已知,则= .
14.已知集合A={x|1≤x<2},B={x|x15.函数在上的最小值与最大值的和为 。
16.若函数满足,求___________..
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17、(本小题满分10分)
已知全集为实数集R,集合,
(I)分别求;
(II)已知集合,若,求实数a的取值范围.
18、 (本小题满分12分) 计算:
19、(本小题满分12分)某公司生产一种电子仪器的固定成本为元,每生产一台仪器需要增加投入元,最大月产量是台。已知总收益满足函数,其中是仪器的月产量(单位:台)。
(1)将利润(单位:元)表示为月产量(单位:台)的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少?(总收益=总成本+利润)。
20、(本小题满分12分)已知函数是定义在R上的偶函数,且当时,.(1)现已画出函数在y轴左侧的图像,如图所示,请补出完整函数的图像,并根据图像写出函数的增区间;
(2)写出函数的解析式和值域.
21、(本小题满分12分)已知函数f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定义域;
(2)若不等式f(x)≤c恒成立,求实数c的取值范围.
22、(本小题满分12分)已知是定义在上的奇函数.
(1)若,求的值;
(2)若是函数的一个零点,求函数在区间的值域.
期中考试高一数学答案
一选择题
1-5 DCBDA 6-10 BCACA 11-12 CD
二 填空题
13.3 14. a≥2 15.1 16.
三 解答题
17. 【解析】:
(I),…………………………………2分
. ……………………5分
(Ⅱ)①当时,,此时; ………………7分
②时,,则. ………………………………9分
综合①②,可得a的取值范围是. …………………………10分
18. (1)原式;
(2)原式=lg5+lg2+-2= -
【解析】:(1)设月产量为台时,利润为元,则总成本为元,
所以 ---------6分
由(1)得
当时, 有最大值----------------------------------------11分
即当月产量为台时,公司获得最大利润为元。------12分
20. 【解析】: (1)因为函数为偶函数,故图象关于y轴对称,补出完整函数图象如有图:
所以f(x)的递增区间是(﹣1,0),(1,+∞).
(2)设x>0,则﹣x<0,所以f(﹣x)=x2﹣2x,因为f(x)是定义在R上的偶函数,所以f(﹣x)=f(x),所以x>0时,f(x)=x2﹣2x,
故f(x)的解析式为
值域为{y|y≥﹣1}
21. 【解析】:(1)∵f(1)=loga2+loga2=2,解得a=2.
∴f(x)=log2(x+1)+log2(3﹣x),
由,解得﹣1<x<3,
可得函数f(x)的定义域为:(﹣1,3).
(2)由(1)可知:f(x)=log2(x+1)+log2(3﹣x)=log2(x+1)(3﹣x)==,
可知:当x=1时,函数f(x)取得最大值,f(1)=log24=2.
由不等式f(x)≤c的恒成立,∴c≥2.
∴实数c的取值范围是[2,+∞).
22.【解析】:(1) 由 f(x)为奇函数,则(b-3)+(b-1)=0,解得.B=2
又 .所以4a+2 =6, ∴a=1 …………6分
(2)由条件知,f(-1)=0,∴a+2=0,∴a=-2
即f(x)=-2x+2/x,可见f(x)在区间[2,4]上单调递减。
所以f(x)的最大值为f(2)=-3,最小值为f(4)=-7.5
故f(x)的值域为[-7.5,-3]. …………12分
(本试卷150分,120分钟)
一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设全集,集合,,则( )
A. B. C. D.
2.已知集合,则下列式子表示正确的有( )
① ② ③ ④
A.1个 B.2个 C.3个 D.4个
3.函数的定义域为( )
A. B. C. D.
4.已知函数,则的值等于( )
A.4 B.2 C.1 D.0
5.已知幂函数y=f(x)的图象经过点(2,),则f(4)的值为( )
A. B.2 C. D.16
6.若函数在区间上是减函数,则实数的取值范围是( )
A. B. C. D.
7.计算:( )
A.2 B.6 C. 8 D. 12
8.已知函数f(x)=ax(a>0,a≠1)在[1,2]上的最大值和最小值的和为6,则a=( )
A.2 B.3 C.4 D.5
9.若a=log20.5,b=20.5,c=0.52,则a,b,c三个数的大小关系是( )
A.a<b<c B.b<c<a C.a<c<b D.c<a<b[
10.函数的大致图象是( )
11.已知 是上的减函数,那么的取值范围是( )
(A) (B)(C) (D)
12. 设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使f(x)<0的x的取值范围为 ( )
A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)
C.(-∞,-1)∪(1,+∞) D.(-1,0)∪(0,1)
宿州市汴北三校2017—2018学年度第一学期期中考试
高一数学答题卡
一选择题;(每题5分,共60分)
题号
1
2
3
4
5
6
答案
题号
7
8
9
10
11
12
答案
二.填空题(本大题共4小题,每小题5分,共20分,请把答案填在答题纸的横线上)
13.已知,则= .
14.已知集合A={x|1≤x<2},B={x|x
16.若函数满足,求___________..
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17、(本小题满分10分)
已知全集为实数集R,集合,
(I)分别求;
(II)已知集合,若,求实数a的取值范围.
18、 (本小题满分12分) 计算:
19、(本小题满分12分)某公司生产一种电子仪器的固定成本为元,每生产一台仪器需要增加投入元,最大月产量是台。已知总收益满足函数,其中是仪器的月产量(单位:台)。
(1)将利润(单位:元)表示为月产量(单位:台)的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少?(总收益=总成本+利润)。
20、(本小题满分12分)已知函数是定义在R上的偶函数,且当时,.(1)现已画出函数在y轴左侧的图像,如图所示,请补出完整函数的图像,并根据图像写出函数的增区间;
(2)写出函数的解析式和值域.
21、(本小题满分12分)已知函数f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定义域;
(2)若不等式f(x)≤c恒成立,求实数c的取值范围.
22、(本小题满分12分)已知是定义在上的奇函数.
(1)若,求的值;
(2)若是函数的一个零点,求函数在区间的值域.
期中考试高一数学答案
一选择题
1-5 DCBDA 6-10 BCACA 11-12 CD
二 填空题
13.3 14. a≥2 15.1 16.
三 解答题
17. 【解析】:
(I),…………………………………2分
. ……………………5分
(Ⅱ)①当时,,此时; ………………7分
②时,,则. ………………………………9分
综合①②,可得a的取值范围是. …………………………10分
18. (1)原式;
(2)原式=lg5+lg2+-2= -
【解析】:(1)设月产量为台时,利润为元,则总成本为元,
所以 ---------6分
由(1)得
当时, 有最大值----------------------------------------11分
即当月产量为台时,公司获得最大利润为元。------12分
20. 【解析】: (1)因为函数为偶函数,故图象关于y轴对称,补出完整函数图象如有图:
所以f(x)的递增区间是(﹣1,0),(1,+∞).
(2)设x>0,则﹣x<0,所以f(﹣x)=x2﹣2x,因为f(x)是定义在R上的偶函数,所以f(﹣x)=f(x),所以x>0时,f(x)=x2﹣2x,
故f(x)的解析式为
值域为{y|y≥﹣1}
21. 【解析】:(1)∵f(1)=loga2+loga2=2,解得a=2.
∴f(x)=log2(x+1)+log2(3﹣x),
由,解得﹣1<x<3,
可得函数f(x)的定义域为:(﹣1,3).
(2)由(1)可知:f(x)=log2(x+1)+log2(3﹣x)=log2(x+1)(3﹣x)==,
可知:当x=1时,函数f(x)取得最大值,f(1)=log24=2.
由不等式f(x)≤c的恒成立,∴c≥2.
∴实数c的取值范围是[2,+∞).
22.【解析】:(1) 由 f(x)为奇函数,则(b-3)+(b-1)=0,解得.B=2
又 .所以4a+2 =6, ∴a=1 …………6分
(2)由条件知,f(-1)=0,∴a+2=0,∴a=-2
即f(x)=-2x+2/x,可见f(x)在区间[2,4]上单调递减。
所以f(x)的最大值为f(2)=-3,最小值为f(4)=-7.5
故f(x)的值域为[-7.5,-3]. …………12分
同课章节目录
