高中数学新人教B版选修1-1课件:第三章导数及其应用章末复习(28张PPT)
文档属性
| 名称 | 高中数学新人教B版选修1-1课件:第三章导数及其应用章末复习(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 538.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-02 00:00:00 | ||
图片预览







文档简介
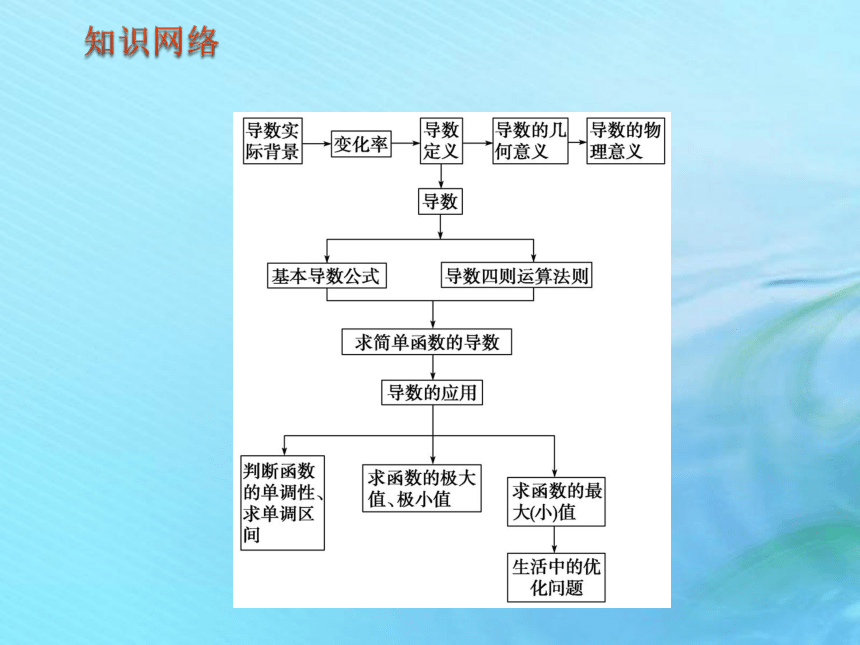
课件28张PPT。第三章 导数及其应用章末复习知识网络专题归纳专题二 导数的几何意义
函数y=f(x)在点x0处的导数的几何意义是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.也就是说,曲线y=f(x)在点P(x0,f(x0))处的切线的斜率为f′(x0),相应的切线方程为y-y0=f′(x0)(x-x0). 已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;
解:(1)由f(x)=x3+x-16,可得f′(x)=3x2+1,所以在点(2,-6)处的切线的斜率为k=f′(2)=13,故切线的方程为y+6=13(x-2),即y=13x-32.
专题三 利用导数研究函数的单调区间
应用导数求函数的单调区间的步骤:
(1)确定函数的定义域;
(2)求导数f′(x);
(3)解不等式f′(x)>0或f′(x)<0;
(4)确定并指出函数的单调增区间、减区间.
特别要注意写单调区间时,区间之间用“和”或“,”隔开,绝对不能用“∪”连结.
已知函数f(x)=4x3+3tx2-6t2x+t-1,x∈R,
其中t∈R.
(1)当t=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)当t>0时,求f(x)的单调区间.
专题四 利用导数研究函数的极值和最值
1.应用导数求函数极值的一般步骤:
(1)确定函数f(x)的定义域;
(2)解方程f′(x)=0的根;
(3)检验f′(x)=0的根的两侧f′(x)的符号.
若左正右负,则f(x)在此根处取得极大值;
若左负右正,则f(x)在此根处取得极小值;
否则,此根不是f(x)的极值点.
2.求函数f(x)在闭区间[a,b]上的最大值、最小值的方法与步骤:
(1)求f(x)在(a,b)内的极值;
(2)将(1)求得的极值与f(a)、f(b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.
特别地,①当f(x)在[a,b]上单调时,其最小值、最大值在区间端点处取得;②当f(x)在(a,b)内只有一个极值点时,
若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取得最大(或最小)值,这里(a,b)也可以是(-∞,+∞).
已知函数f(x)=x3-3x2-2.若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
解:对函数f(x)求导,f′(x)=3x2-6x=3x(x-2),令f′(x)=0,得x=0或x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
对a分四种情况讨论:
①当0综上可得,当0专题五 导数在实际中的应用问题
利用导数求实际问题的最大(小)值时,应注意的问题:
(1)求实际问题的最大(小)值时,一定要从问题的实际意义去考虑,不符合实际意义的值应舍去.
(2)在实际问题中,由f′(x)=0常常仅解到一个根,若能判断函数的最大(小)值在x的变化区间内部得到,则这个根处的函数值就是所求的最大(小)值.
如图,一矩形铁皮的长为8 cm,宽为5 cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为多少时,盒子容积最大?当x变化时,V′(x),V(x)的变化情况如下表:
∴V极大值=V(1)=18,又在定义域内仅有一个极大值.
∴V最大值=18.
即小正方形的边长为1 cm时,盒子的容积最大,最大为18 cm3.
能力提升【解析】函数f(x)=ex+ax,则f′(x)=ex+a.
若函数在x∈R上有大于零的极值点,
即f′(x)=ex+a=0有正根.
当f′(x)=a+ex=0成立时,显然有a<0,此时x=ln(-a),
由x>0,得参数a的范围为a<-1.
【答案】B2.曲线y=x3+x-2的斜率为4的切线方程是________.【答案】4x-y-4=0或4x-y=03.已知函数f(x)=alnx+x在区间[2,3]上单调递增,则实数a的取值范围是________.【答案】[-2,+∞)
函数y=f(x)在点x0处的导数的几何意义是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.也就是说,曲线y=f(x)在点P(x0,f(x0))处的切线的斜率为f′(x0),相应的切线方程为y-y0=f′(x0)(x-x0). 已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;
解:(1)由f(x)=x3+x-16,可得f′(x)=3x2+1,所以在点(2,-6)处的切线的斜率为k=f′(2)=13,故切线的方程为y+6=13(x-2),即y=13x-32.
专题三 利用导数研究函数的单调区间
应用导数求函数的单调区间的步骤:
(1)确定函数的定义域;
(2)求导数f′(x);
(3)解不等式f′(x)>0或f′(x)<0;
(4)确定并指出函数的单调增区间、减区间.
特别要注意写单调区间时,区间之间用“和”或“,”隔开,绝对不能用“∪”连结.
已知函数f(x)=4x3+3tx2-6t2x+t-1,x∈R,
其中t∈R.
(1)当t=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)当t>0时,求f(x)的单调区间.
专题四 利用导数研究函数的极值和最值
1.应用导数求函数极值的一般步骤:
(1)确定函数f(x)的定义域;
(2)解方程f′(x)=0的根;
(3)检验f′(x)=0的根的两侧f′(x)的符号.
若左正右负,则f(x)在此根处取得极大值;
若左负右正,则f(x)在此根处取得极小值;
否则,此根不是f(x)的极值点.
2.求函数f(x)在闭区间[a,b]上的最大值、最小值的方法与步骤:
(1)求f(x)在(a,b)内的极值;
(2)将(1)求得的极值与f(a)、f(b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.
特别地,①当f(x)在[a,b]上单调时,其最小值、最大值在区间端点处取得;②当f(x)在(a,b)内只有一个极值点时,
若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取得最大(或最小)值,这里(a,b)也可以是(-∞,+∞).
已知函数f(x)=x3-3x2-2.若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
解:对函数f(x)求导,f′(x)=3x2-6x=3x(x-2),令f′(x)=0,得x=0或x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
对a分四种情况讨论:
①当0
利用导数求实际问题的最大(小)值时,应注意的问题:
(1)求实际问题的最大(小)值时,一定要从问题的实际意义去考虑,不符合实际意义的值应舍去.
(2)在实际问题中,由f′(x)=0常常仅解到一个根,若能判断函数的最大(小)值在x的变化区间内部得到,则这个根处的函数值就是所求的最大(小)值.
如图,一矩形铁皮的长为8 cm,宽为5 cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为多少时,盒子容积最大?当x变化时,V′(x),V(x)的变化情况如下表:
∴V极大值=V(1)=18,又在定义域内仅有一个极大值.
∴V最大值=18.
即小正方形的边长为1 cm时,盒子的容积最大,最大为18 cm3.
能力提升【解析】函数f(x)=ex+ax,则f′(x)=ex+a.
若函数在x∈R上有大于零的极值点,
即f′(x)=ex+a=0有正根.
当f′(x)=a+ex=0成立时,显然有a<0,此时x=ln(-a),
由x>0,得参数a的范围为a<-1.
【答案】B2.曲线y=x3+x-2的斜率为4的切线方程是________.【答案】4x-y-4=0或4x-y=03.已知函数f(x)=alnx+x在区间[2,3]上单调递增,则实数a的取值范围是________.【答案】[-2,+∞)
