高二数学课件:选修2-2 1.5.1 曲边梯形的面积 共38张PPT
文档属性
| 名称 | 高二数学课件:选修2-2 1.5.1 曲边梯形的面积 共38张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 542.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-03 00:00:00 | ||
图片预览



文档简介
课件38张PPT。 1.5.1 曲边梯形
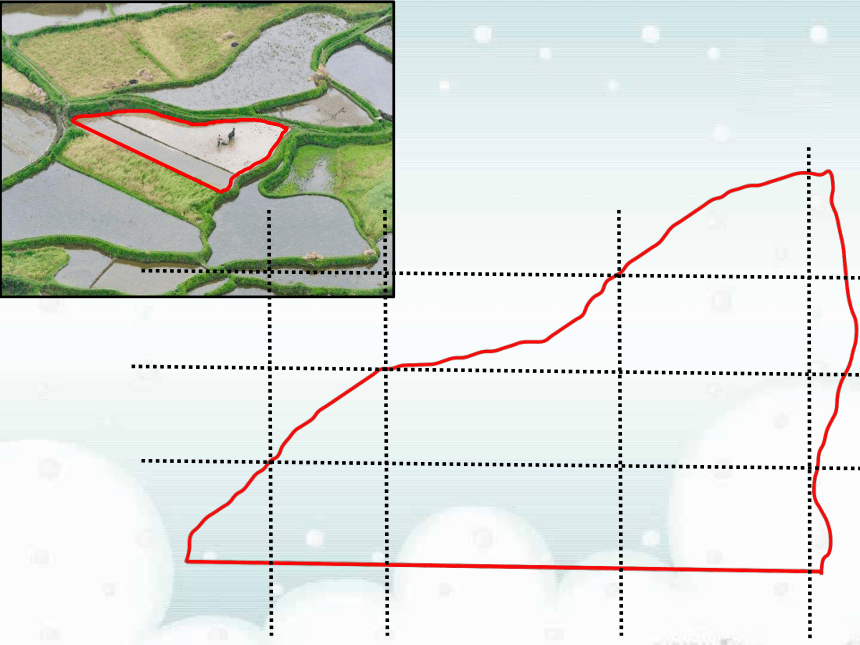
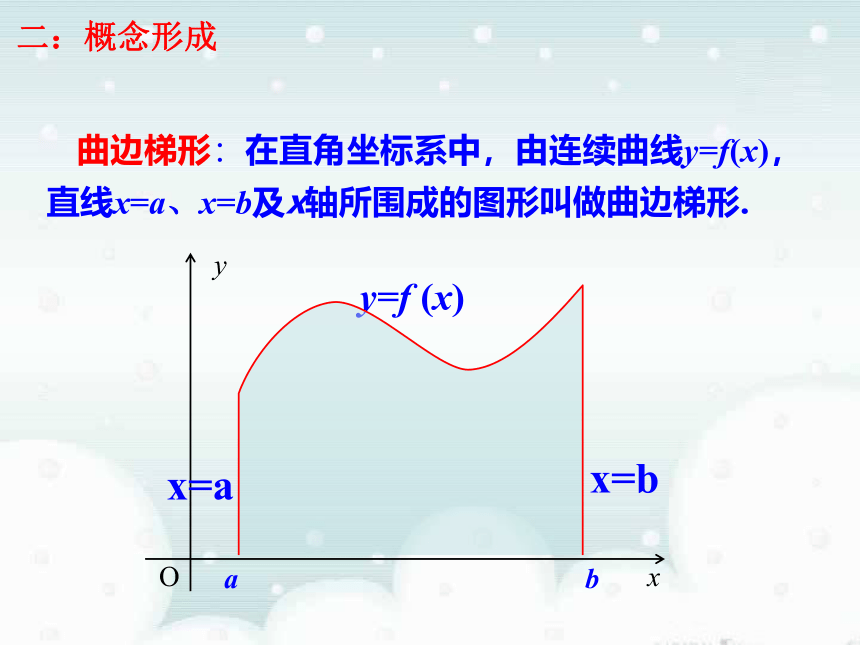
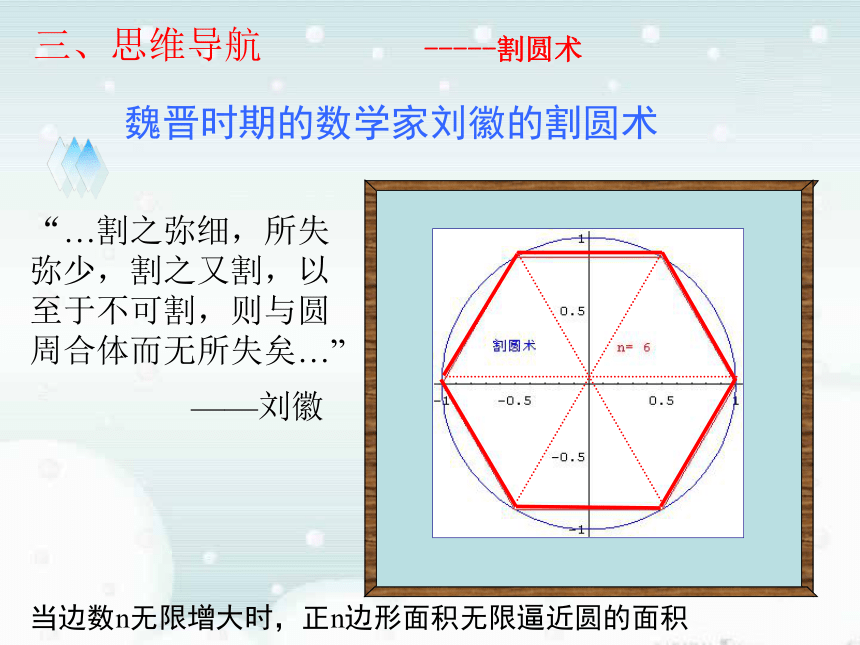
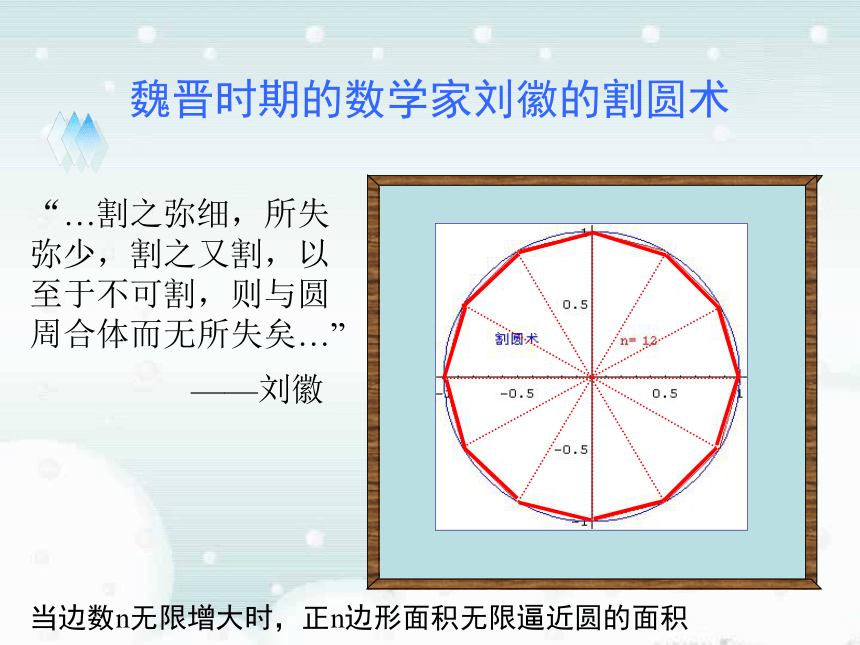
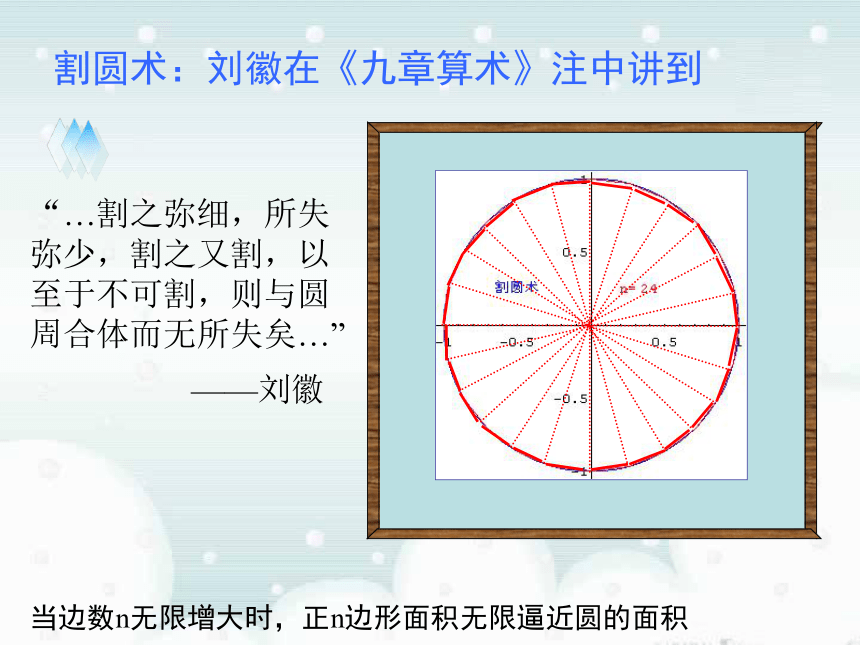
的面积一、新课导入 曲边梯形:在直角坐标系中,由连续曲线y=f(x),直线x=a、x=b及x轴所围成的图形叫做曲边梯形.Ox y y=f (x)x=ax=b二:概念形成魏晋时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽三、思维导航-----割圆术当边数n无限增大时,正n边形面积无限逼近圆的面积魏晋时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”割圆术:刘徽在《九章算术》注中讲到——刘徽
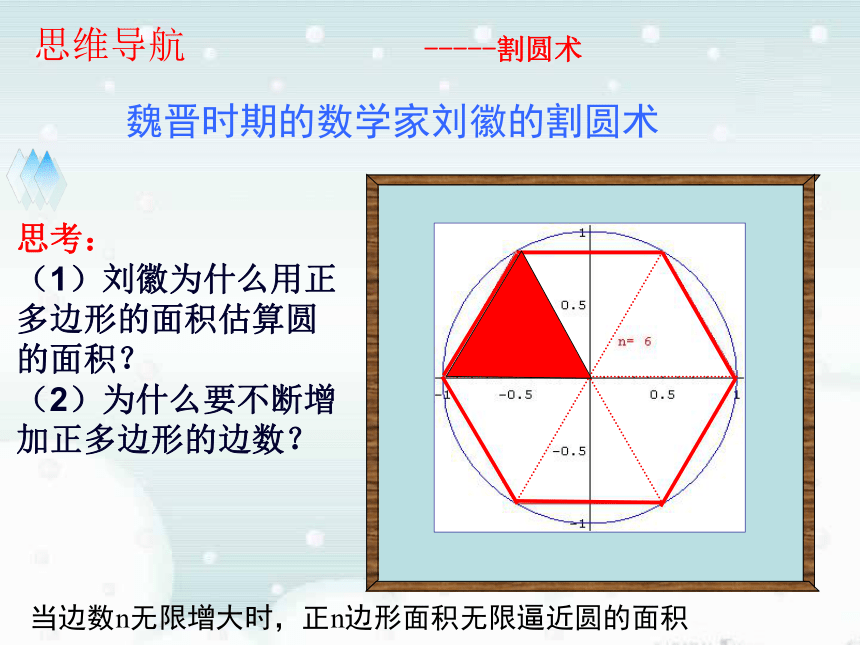
当边数n无限增大时,正n边形面积无限逼近圆的面积魏晋时期的数学家刘徽的割圆术思维导航-----割圆术思考: (1)刘徽为什么用正多边形的面积估算圆的面积? (2)为什么要不断增加正多边形的边数?
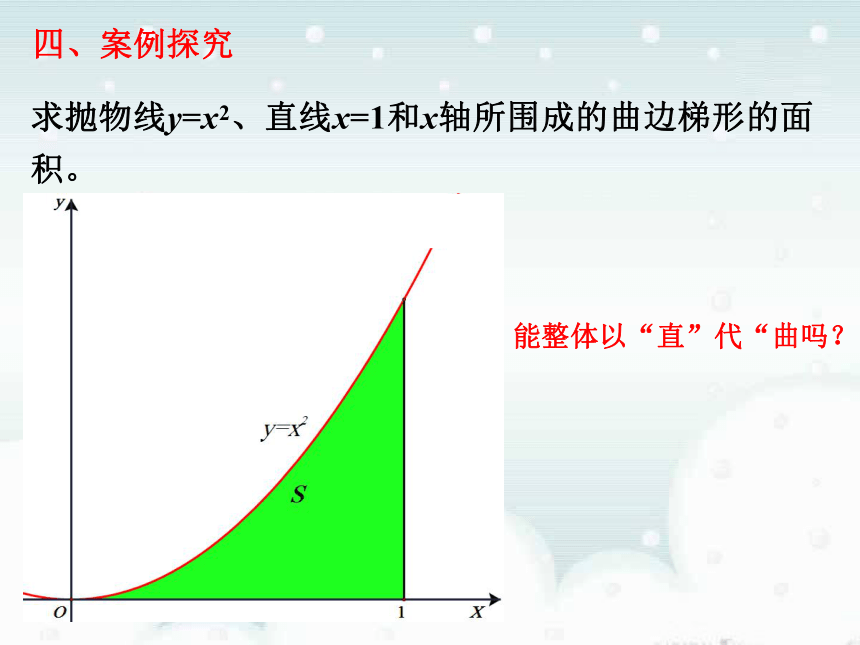
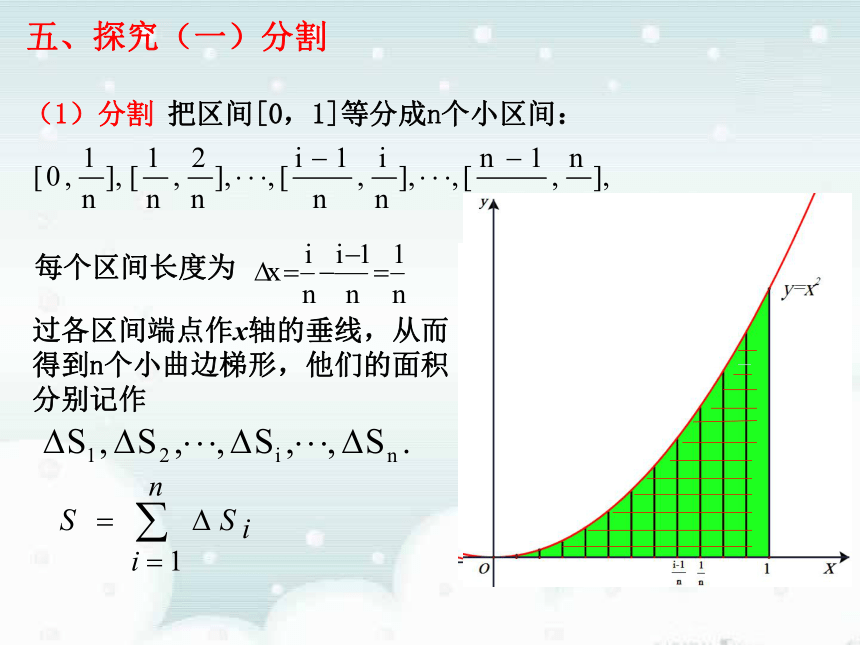
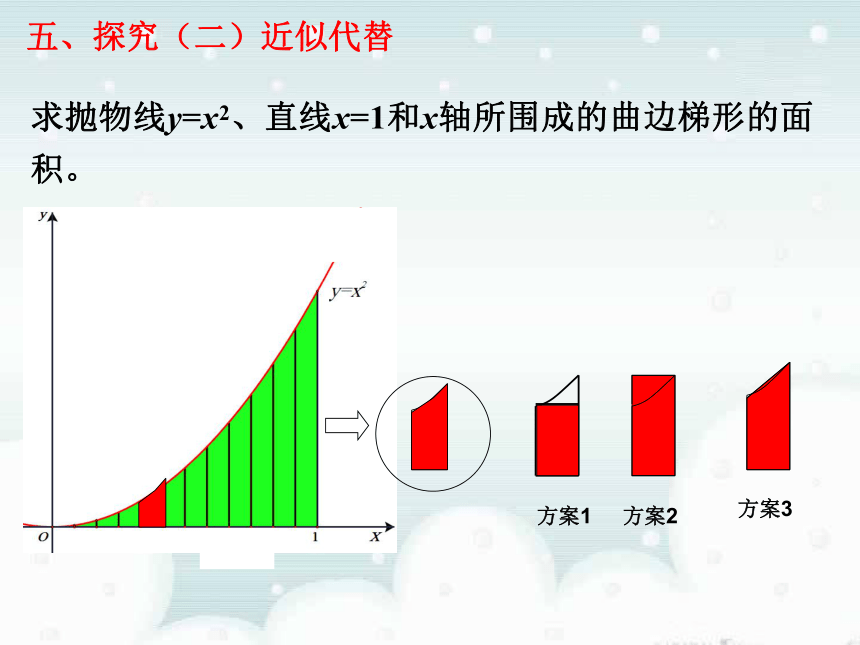
当边数n无限增大时,正n边形面积无限逼近圆的面积求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积。四、案例探究能整体以“直”代“曲吗?(1)分割把区间[0,1]等分成n个小区间:过各区间端点作x轴的垂线,从而得到n个小曲边梯形,他们的面积分别记作每个区间长度为五、探究(一)分割求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积。方案2方案3方案1五、探究(二)近似代替
方案2方案3方案1五、探究(二)近似代替求和五、探究(三)求和当n无限增大,即分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S.五、探究(四)取极限不断增加n的值,观察下列表格,体会逼近的思想。点击演示求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积。方案2方案3方案1五、探究方案3方案1方案2 五、探究一般曲边梯形的面积的表达式 求直线x=0,x=2,y=0与曲线 所围成的曲边梯形的面积。 (1)分割:将它等分成n个小区间: 每个小区间宽度:(2)近似代替:(3) 求和:(4)取极限:六、练习学习共勉:饱学经纶应视细节为径,
胸怀大志当以小事作梯。1.主要学习了:求曲边梯形的面积等份分割易操作
以直代曲好求和
无限逼近取极限
微分学习尽把握2.初步了解了:以直代曲转化思想,无限逼近极限思想.观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。返回
的面积一、新课导入 曲边梯形:在直角坐标系中,由连续曲线y=f(x),直线x=a、x=b及x轴所围成的图形叫做曲边梯形.Ox y y=f (x)x=ax=b二:概念形成魏晋时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽三、思维导航-----割圆术当边数n无限增大时,正n边形面积无限逼近圆的面积魏晋时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”割圆术:刘徽在《九章算术》注中讲到——刘徽
当边数n无限增大时,正n边形面积无限逼近圆的面积魏晋时期的数学家刘徽的割圆术思维导航-----割圆术思考: (1)刘徽为什么用正多边形的面积估算圆的面积? (2)为什么要不断增加正多边形的边数?
当边数n无限增大时,正n边形面积无限逼近圆的面积求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积。四、案例探究能整体以“直”代“曲吗?(1)分割把区间[0,1]等分成n个小区间:过各区间端点作x轴的垂线,从而得到n个小曲边梯形,他们的面积分别记作每个区间长度为五、探究(一)分割求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积。方案2方案3方案1五、探究(二)近似代替
方案2方案3方案1五、探究(二)近似代替求和五、探究(三)求和当n无限增大,即分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S.五、探究(四)取极限不断增加n的值,观察下列表格,体会逼近的思想。点击演示求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积。方案2方案3方案1五、探究方案3方案1方案2 五、探究一般曲边梯形的面积的表达式 求直线x=0,x=2,y=0与曲线 所围成的曲边梯形的面积。 (1)分割:将它等分成n个小区间: 每个小区间宽度:(2)近似代替:(3) 求和:(4)取极限:六、练习学习共勉:饱学经纶应视细节为径,
胸怀大志当以小事作梯。1.主要学习了:求曲边梯形的面积等份分割易操作
以直代曲好求和
无限逼近取极限
微分学习尽把握2.初步了解了:以直代曲转化思想,无限逼近极限思想.观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。返回
