19.1.1 矩形的性质 课件 (19张PPT)
文档属性
| 名称 | 19.1.1 矩形的性质 课件 (19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 319.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-03 14:31:16 | ||
图片预览


文档简介
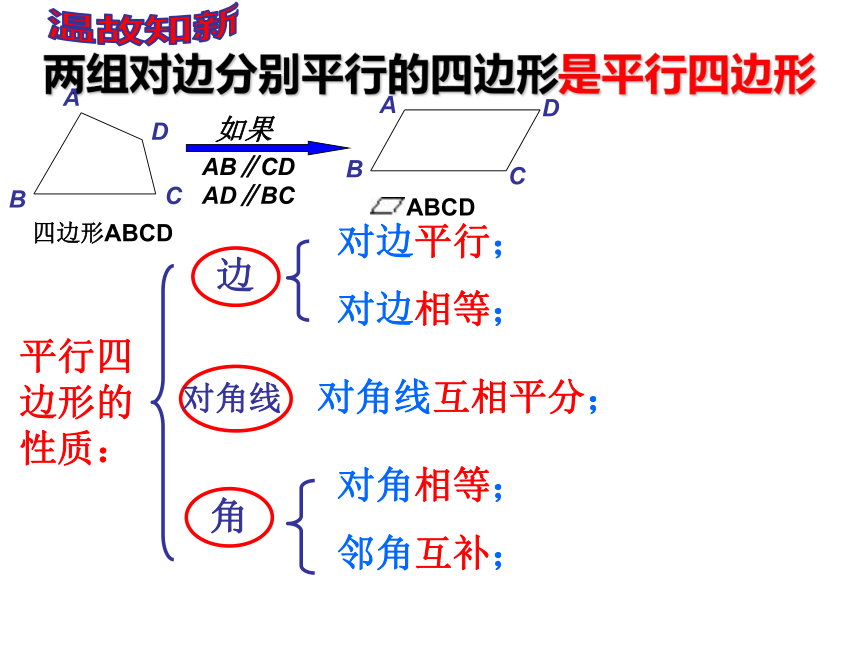
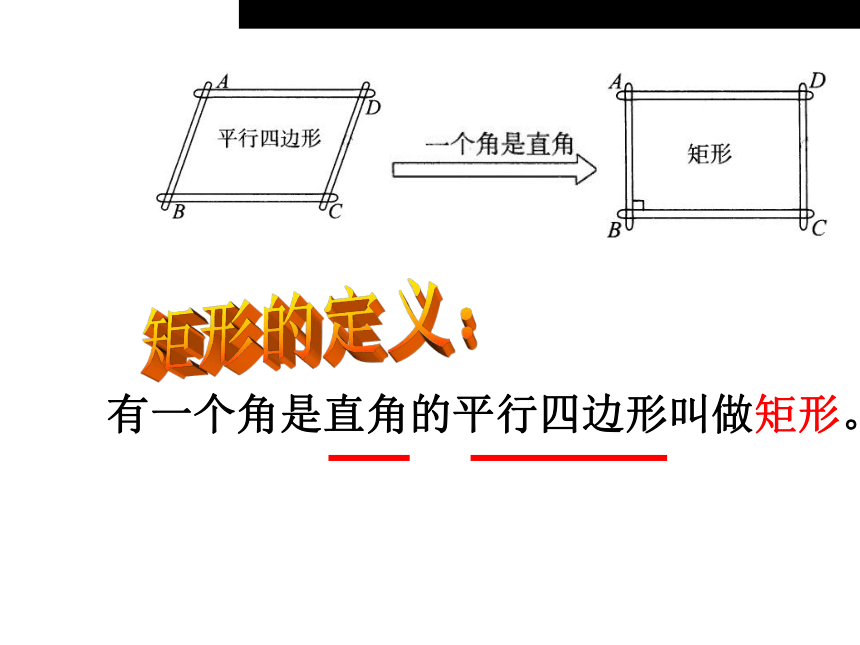
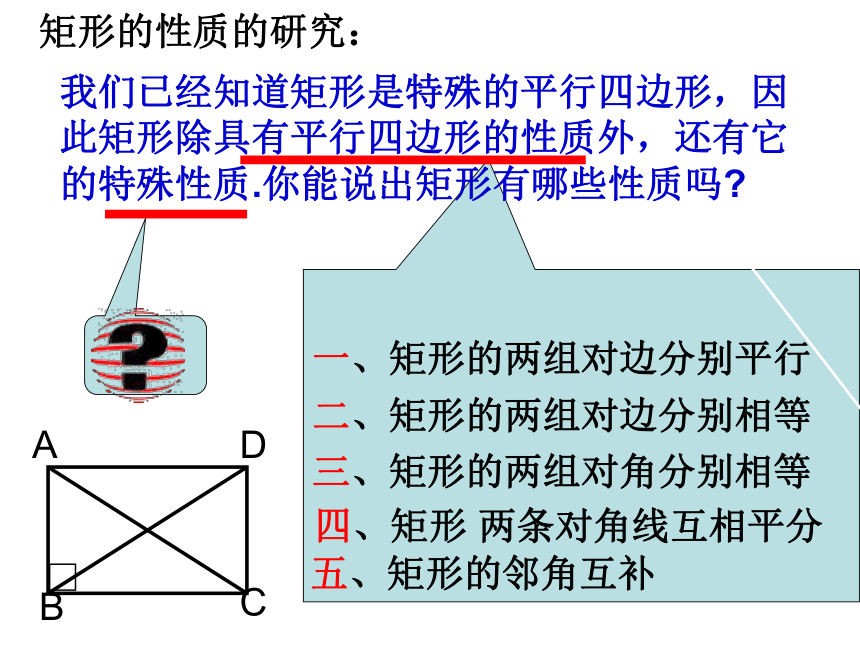
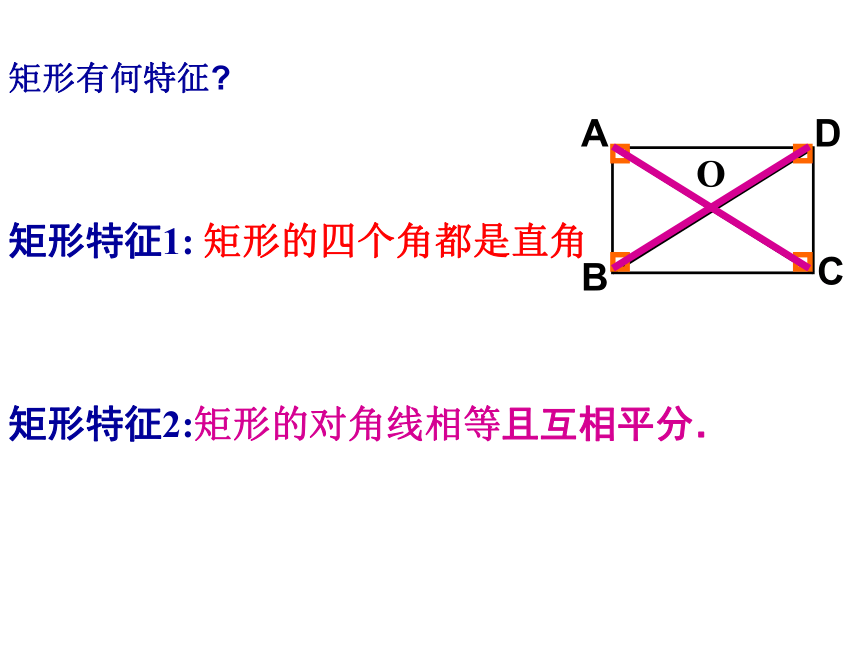
课件19张PPT。19.2.1矩形的性质两组对边分别平行的四边形是平行四边形平行四边形的性质:对边平行;对边相等;对角相等;邻角互补;对角线互相平分; 温故知新第五节矩形菱形有一个角是直角的平行四边形叫做矩形。矩形的定义:矩形的性质的研究:我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补矩形有何特征?矩形特征1: 矩形的四个角都是直角矩形特征2:矩形的对角线相等且互相平分. 命题1:矩形的四个角都是直角;已知:四边形ABCD是矩形 ∠C=90°
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
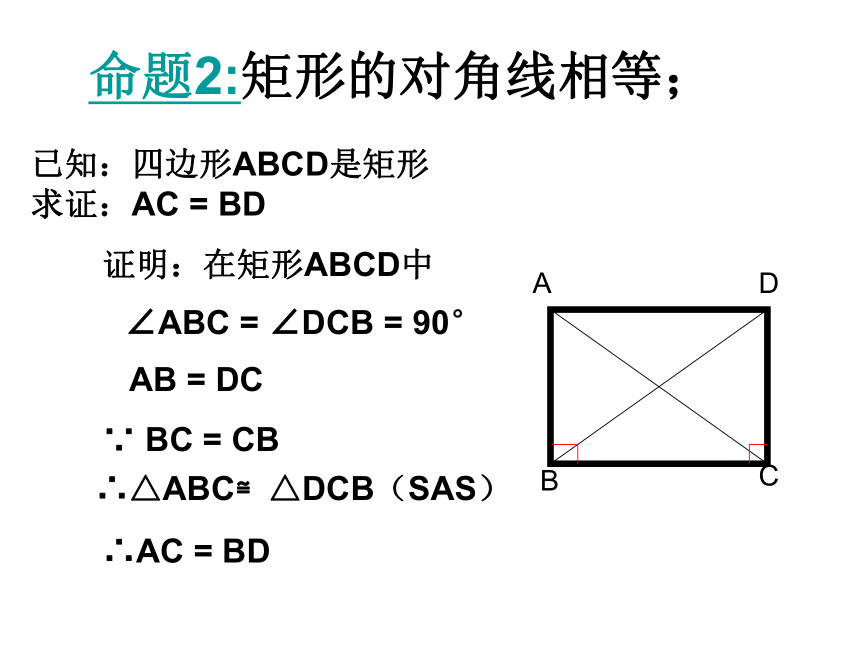
求证:AC = BD证明:在矩形ABCD中∠ABC = ∠DCB = 90° AB = DC
∵ BC = CB∴△ABC≌△DCB(SAS)∴AC = BD命题2:矩形的对角线相等;矩形与平行四边形的性质对比两条对角线相等且互相平分两条对角线互相平分对角线每一个角都是90°对角相等,邻角互补角两组对边平行且相等两组对边平行且相等边矩形平行四边形性质邻边:互相垂直四个角都是直角 互相平分
相 等
(1)边:(2)角:(3)对角线:对边:平行
相等
(共性)(共性)(个性)(个性)(个性)(共性)O矩形特征直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半. 如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系探究:推论:直角三角形斜边上的中线等于斜边的一半.已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB证明:延长CD到E使DE=CD,
连结AE、BE.∵AD = BD , DE =CD
∴四边形ACBE是平行四边形E?思考:矩形ABCD是轴对称图形吗?它的对称轴有几条?矩形是中心对称图形吗?对称中心是?ABCDEFGH.例1:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
例2: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵四边形ABCD是矩形
∴ OA=OB
∵∠AOB=60° ∴△AOB是等边三角形
∴OA=AB=4(㎝)
∴矩形的对角线长 AC=BD=2OA=8(㎝)AD=4cm四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则 ∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝, 则AC= ㎝550°10100°40°12482880°试一试5 已知△ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线(1)若BD=3㎝ 则 AC= ㎝
(2)若∠C=30°,AB=5㎝,则 AC= ㎝,
BD= ㎝, ∠BDC=6510120°D1. 在Rt⊿ABC中,
∠C=90°,AB=2AC.
求∠ A 、 ∠B 的度数.作斜边AB边的中线则 AD=CD= AB∴AC=AD=CD= AB∵AB=2AC∴⊿ACD是等边三角形 ∴∠A=60°
∴∠B=30 °练习如图四边形ABCD中,∠ABC=∠ADC=900,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。能力提升:再 见
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∠ABC = ∠DCB = 90° AB = DC
∵ BC = CB∴△ABC≌△DCB(SAS)∴AC = BD命题2:矩形的对角线相等;矩形与平行四边形的性质对比两条对角线相等且互相平分两条对角线互相平分对角线每一个角都是90°对角相等,邻角互补角两组对边平行且相等两组对边平行且相等边矩形平行四边形性质邻边:互相垂直四个角都是直角 互相平分
相 等
(1)边:(2)角:(3)对角线:对边:平行
相等
(共性)(共性)(个性)(个性)(个性)(共性)O矩形特征直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半. 如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系探究:推论:直角三角形斜边上的中线等于斜边的一半.已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB证明:延长CD到E使DE=CD,
连结AE、BE.∵AD = BD , DE =CD
∴四边形ACBE是平行四边形E?思考:矩形ABCD是轴对称图形吗?它的对称轴有几条?矩形是中心对称图形吗?对称中心是?ABCDEFGH.例1:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
例2: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵四边形ABCD是矩形
∴ OA=OB
∵∠AOB=60° ∴△AOB是等边三角形
∴OA=AB=4(㎝)
∴矩形的对角线长 AC=BD=2OA=8(㎝)AD=4cm四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则 ∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝, 则AC= ㎝550°10100°40°12482880°试一试5 已知△ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线(1)若BD=3㎝ 则 AC= ㎝
(2)若∠C=30°,AB=5㎝,则 AC= ㎝,
BD= ㎝, ∠BDC=6510120°D1. 在Rt⊿ABC中,
∠C=90°,AB=2AC.
求∠ A 、 ∠B 的度数.作斜边AB边的中线则 AD=CD= AB∴AC=AD=CD= AB∵AB=2AC∴⊿ACD是等边三角形 ∴∠A=60°
∴∠B=30 °练习如图四边形ABCD中,∠ABC=∠ADC=900,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。能力提升:再 见
