19.2.1 菱形的性质课件(16张PPT)
文档属性
| 名称 | 19.2.1 菱形的性质课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-03 00:00:00 | ||
图片预览



文档简介
课件16张PPT。19.2 菱形
1.菱形的性质
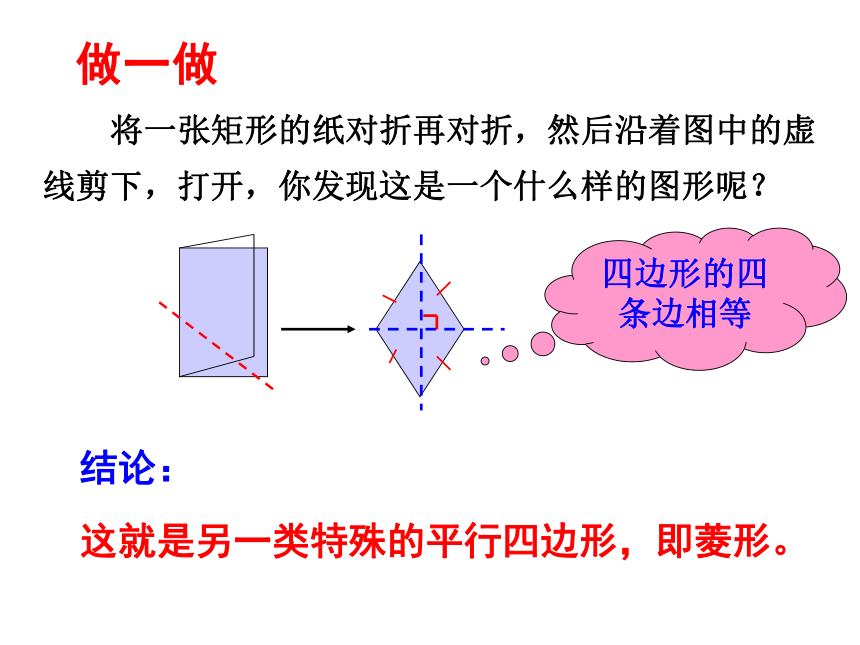
八年级下册平行四边形有哪些特征?矩形与平行四边形比较有哪些特殊的特征?平行四边形边:角:对角线:对边平行且相等对角相等邻角互补对角线互相平分矩形角:四个角是直角对角线:对角线相等观察图案,有没有你熟悉的图形?做一做结论:
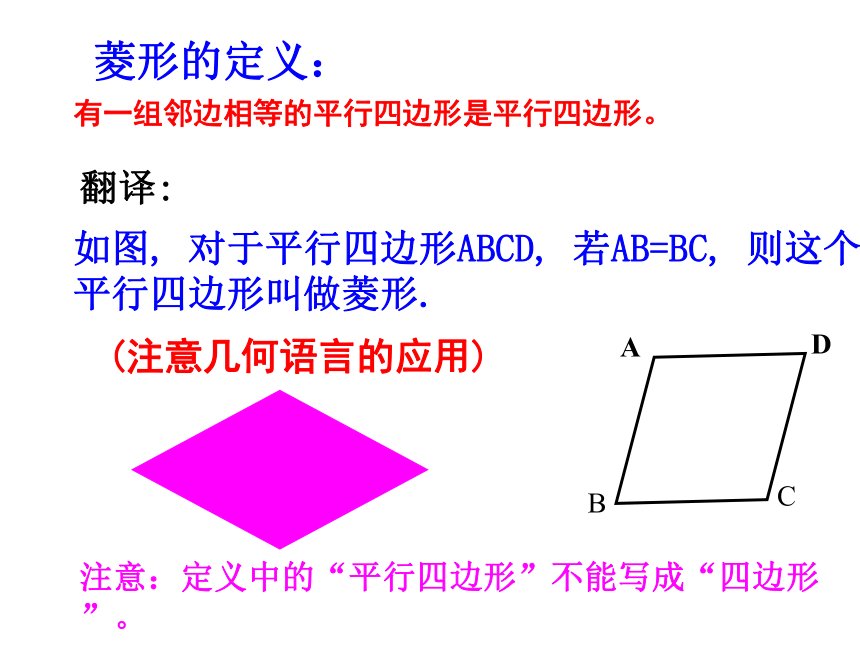
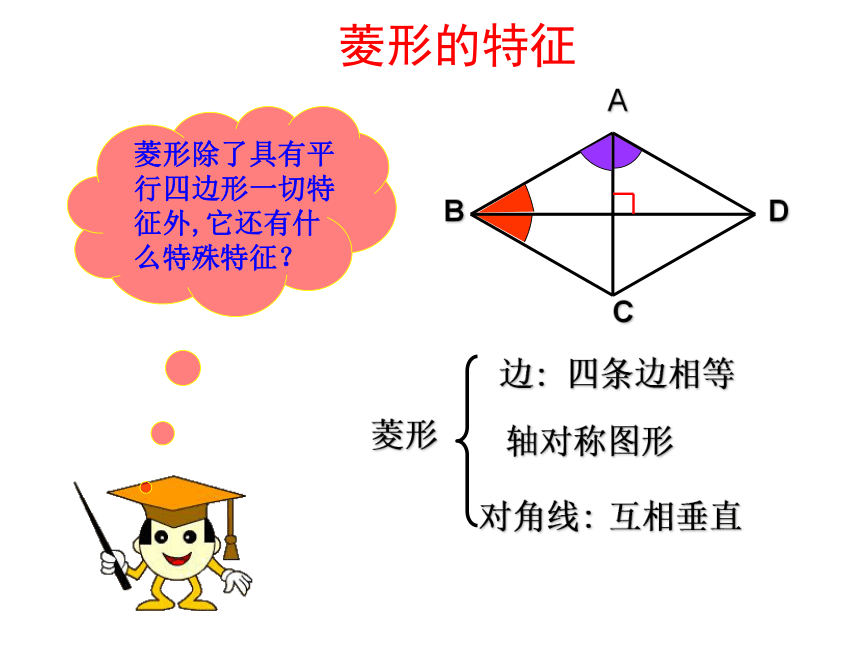
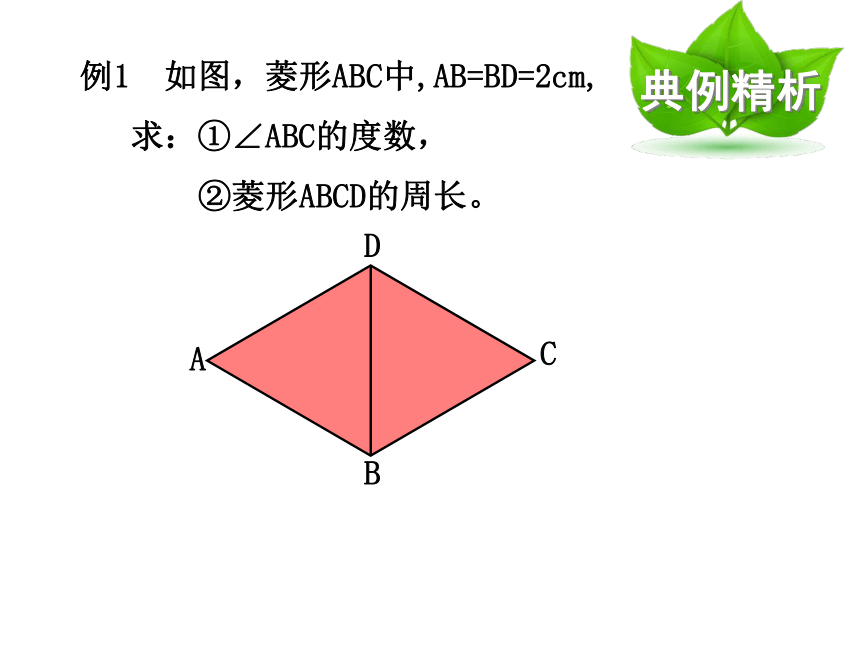
这就是另一类特殊的平行四边形,即菱形。 将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?四边形的四条边相等有一组邻边相等的平行四边形是平行四边形。菱形的定义:翻译:如图, 对于平行四边形ABCD, 若AB=BC, 则这个平行四边形叫做菱形.(注意几何语言的应用)注意:定义中的“平行四边形”不能写成“四边形”。菱形除了具有平行四边形一切特征外,它还有什么特殊特征?菱形边:四条边相等对角线:互相垂直轴对称图形ABCD菱形的特征例1 如图,菱形ABC中,AB=BD=2cm,
求:①∠ABC的度数,
②菱形ABCD的周长。解:①∵菱形ABCD
∴AB=AD(菱形的四条边都相等)又 ∵AB=BD(已知)
∴在△ABD中,
AB=AD=BD
即 △ABD是等边三角形
∴∠ABD=60°∴ ∠ABC=2∠ABD=120°(菱形对角线平分对角)②∵菱形ABCD
∴AB=BC=CD=DA ∴菱形ABCD的周长 = 2×4 = 8 cm 例2:如图,在菱形ABCD中,∠BAD=2∠B,试说明△ABC是等边三角形。解:由于菱形是一类特殊的平行四边形,
所以 AB=BC
∠B+∠BAD=180°
又已知 ∠BAD=2∠B
可得 ∠B=60°
所以△ABC是一个角为60°的等腰三角形,即为等边三角形。 例3 如图,在菱形ABCD中,AC与BD相交于点O,AB=5,OA=4,求这一菱形的周长与两条对角线的长度。O解:菱形的周长
AB+BC+CD+DA=4AB = 4×5 = 20对角线 AC=2AO=2×4=8,
BD=2BO=2×3=6.在△ABO中,根据勾股定理得O1.一个菱形的周长为8cm,一条对角线长为2 cm.则这个菱形的四个内角的度数为 。
2.菱形具有而平行四边形不一定具有的特征是( )
A、对角线互相平分 B、对边相等且平行
C、对角线平分一组对角 D、对角相等60°、120°、60°、120°C菱形的定义:有一组邻边相等的平行四边形是菱形。 菱形的性质:1.对边平行,且四边都相等;3.对角线互相平分且互相垂直 .2.对角相等;4.菱形既是中心对称图形,又是轴对称图形通过这节课的学习,你有哪些收获?1.从教材习题中选取,
2.完成练习册本课时的习题.
求:①∠ABC的度数,
②菱形ABCD的周长。解:①∵菱形ABCD
∴AB=AD(菱形的四条边都相等)又 ∵AB=BD(已知)
∴在△ABD中,
AB=AD=BD
即 △ABD是等边三角形
∴∠ABD=60°∴ ∠ABC=2∠ABD=120°(菱形对角线平分对角)②∵菱形ABCD
∴AB=BC=CD=DA ∴菱形ABCD的周长 = 2×4 = 8 cm 例2:如图,在菱形ABCD中,∠BAD=2∠B,试说明△ABC是等边三角形。解:由于菱形是一类特殊的平行四边形,
所以 AB=BC
∠B+∠BAD=180°
又已知 ∠BAD=2∠B
可得 ∠B=60°
所以△ABC是一个角为60°的等腰三角形,即为等边三角形。 例3 如图,在菱形ABCD中,AC与BD相交于点O,AB=5,OA=4,求这一菱形的周长与两条对角线的长度。O解:菱形的周长
AB+BC+CD+DA=4AB = 4×5 = 20对角线 AC=2AO=2×4=8,
BD=2BO=2×3=6.在△ABO中,根据勾股定理得O1.一个菱形的周长为8cm,一条对角线长为2 cm.则这个菱形的四个内角的度数为 。
2.菱形具有而平行四边形不一定具有的特征是( )
A、对角线互相平分 B、对边相等且平行
C、对角线平分一组对角 D、对角相等60°、120°、60°、120°C菱形的定义:有一组邻边相等的平行四边形是菱形。 菱形的性质:1.对边平行,且四边都相等;3.对角线互相平分且互相垂直 .2.对角相等;4.菱形既是中心对称图形,又是轴对称图形通过这节课的学习,你有哪些收获?1.从教材习题中选取,
2.完成练习册本课时的习题.
