19.1.1 矩形的性质课件 (17张PPT)
文档属性
| 名称 | 19.1.1 矩形的性质课件 (17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-03 14:43:17 | ||
图片预览


文档简介
课件17张PPT。19.1矩形的性质
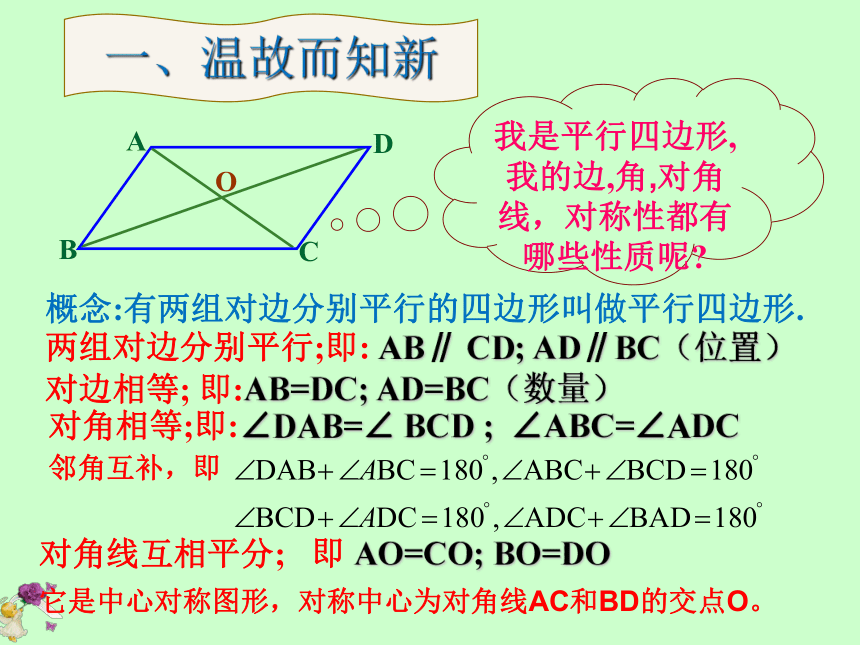
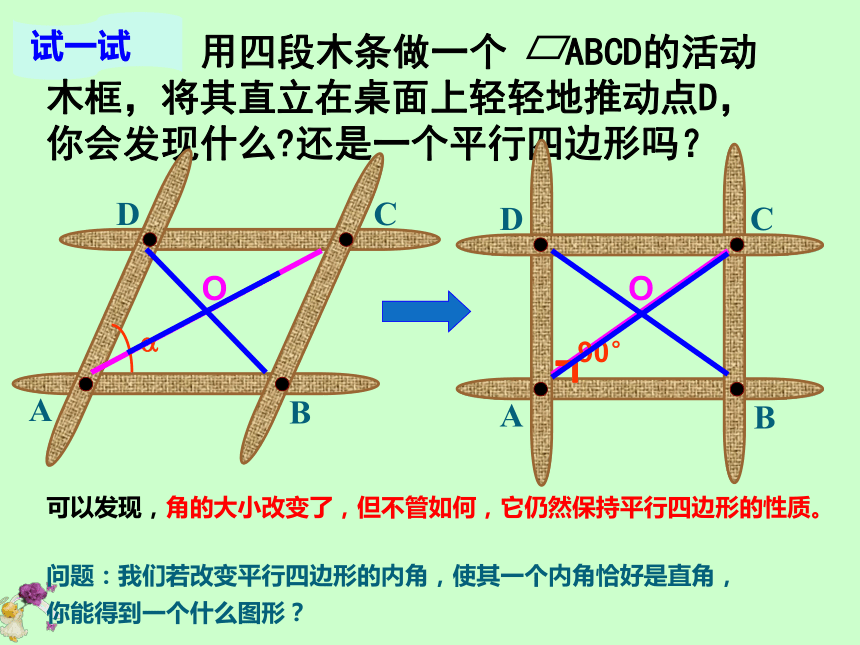
我是平行四边形,我的边,角,对角线,对称性都有哪些性质呢?概念:有两组对边分别平行的四边形叫做平行四边形.O两组对边分别平行;即: AB∥ CD; AD∥BC(位置)对边相等; 即:AB=DC; AD=BC(数量)对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠ADC对角线互相平分;即 AO=CO; BO=DO一、温故而知新它是中心对称图形,对称中心为对角线AC和BD的交点O。邻角互补,即 用四段木条做一个 ABCD的活动 木框,将其直立在桌面上轻轻地推动点D,你会发现什么?还是一个平行四边形吗?试一试?OO┓90°可以发现,角的大小改变了,但不管如何,它仍然保持平行四边形的性质。问题:我们若改变平行四边形的内角,使其一个内角恰好是直角,
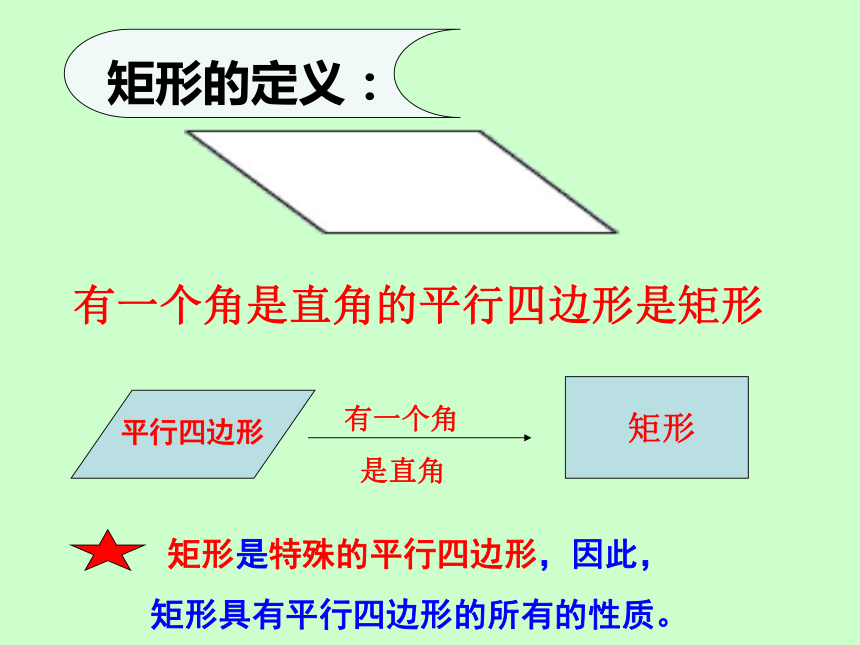
你能得到一个什么图形?有一个角是直角的平行四边形是矩形矩形的定义:1.你认为矩形是轴对称图
形吗?如果是,它有几条
对称轴?试着画出来,并
用对折的方法进行验证.
2.观察角有什么特征?
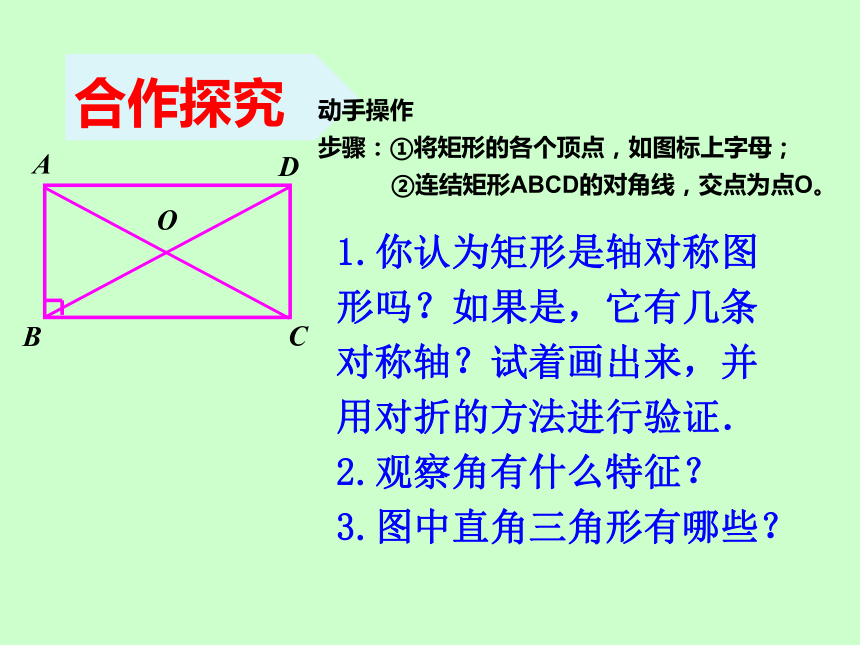
3.图中直角三角形有哪些?O合作探究动手操作
步骤:①将矩形的各个顶点,如图标上字母;
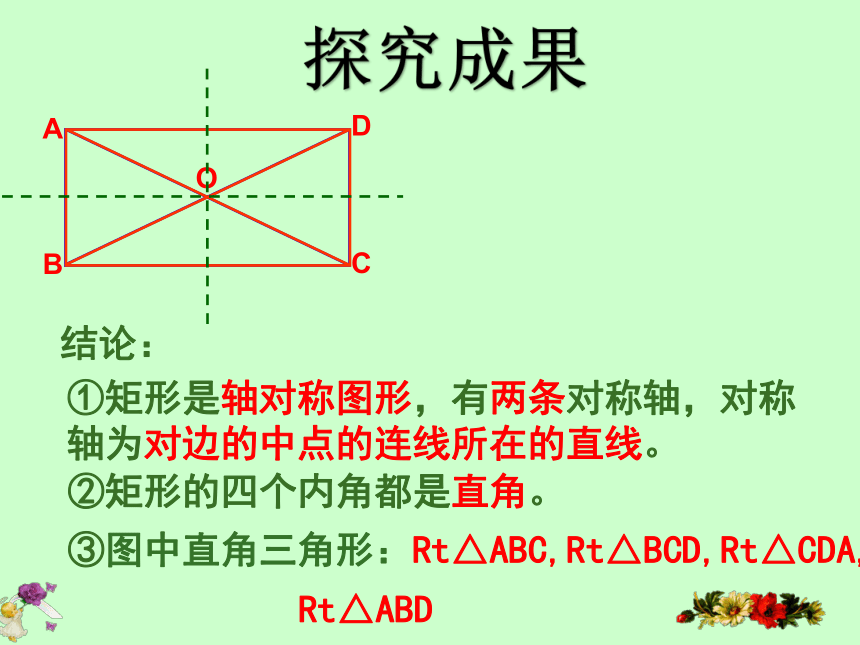
②连结矩形ABCD的对角线,交点为点O。ABCDO结论:①矩形是轴对称图形,有两条对称轴,对称轴为对边的中点的连线所在的直线。②矩形的四个内角都是直角。③图中直角三角形:Rt△ABC,Rt△BCD,Rt△CDA,
Rt△ABD
探究成果4.观察对角线之间有什么
数量关系?
5.图中相等的线段有哪些?
6.图中等腰三角形有哪些?O?????深入探究O探究成果5.相等的线段:
AB=CD,AD=BC, AC=BD,OA=OC=OB=OD;6.等腰三角形:
△AOB,△BOC,△COD,△AOD4.矩形的对角线相等; 比一比,填一填中心对称
图形对边平行
且相等对角相等
邻角互补互相平分
轴对称图形四个内角
都是直角相等证明:矩形的四个角都是直角ABCD证明:在矩形ABCD中,∵AD//BC(两直线平行,同旁内角互补)(已知)(等式的性质)(矩形的对角相等)(等量代换)(矩形的对边平行)矩形的性质定理1: 矩形的四个角都是直角∵四边形ABCD是矩形∴ ∠A=∠B = ∠C=∠D = 90°证明:矩形的对角线相等BADCO已知:在矩形ABCD中,对角线AC和BD相交于点O求证:AC=BD证明:∵四边形ABCD是矩形(已知)∴AB=CD(矩形的对边相等)
∠ABC=∠BCD = 90°(矩形的四个角是直角) ∵BC=CB(公共边)即AC=BD(全等三角形的对应边相等)矩形的性质定理2:矩形的对角线相等.∵四边形ABCD是矩形∴AC=BD 在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,
求AC= ,OB= ,10685小试牛刀矩形具有而一般平行四边形不具有的性质是( )
A对角线相等 B对边相等
C对角相等 D对角线互相平分A巩固新知解:又∵AC=BD=13cm(矩形的对角线相等) ∵△AOB、△BOC、△COD和△AOD四个小三角形的周长和为86 cm(已知)∴AB+BC+CD+DA
=86-2(AC+BD) =86-4×13
=34(cm)即矩形ABCD的周长等于34cm例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)
=86矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2 这节课你学到了什么? 还有什么困惑吗?我的收获知识的升华1.认真复习《矩形的性质》,完成学法大视野的相关练习题。
2.完成教科书P100练习题。跳一跳,够得着!已知:如图,在矩形ABCD中,M为BC的中点.
求证:(2)若要使∠AMD是直角,应添加什
么条件?(1)AM=DM.
谢谢大家!
我是平行四边形,我的边,角,对角线,对称性都有哪些性质呢?概念:有两组对边分别平行的四边形叫做平行四边形.O两组对边分别平行;即: AB∥ CD; AD∥BC(位置)对边相等; 即:AB=DC; AD=BC(数量)对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠ADC对角线互相平分;即 AO=CO; BO=DO一、温故而知新它是中心对称图形,对称中心为对角线AC和BD的交点O。邻角互补,即 用四段木条做一个 ABCD的活动 木框,将其直立在桌面上轻轻地推动点D,你会发现什么?还是一个平行四边形吗?试一试?OO┓90°可以发现,角的大小改变了,但不管如何,它仍然保持平行四边形的性质。问题:我们若改变平行四边形的内角,使其一个内角恰好是直角,
你能得到一个什么图形?有一个角是直角的平行四边形是矩形矩形的定义:1.你认为矩形是轴对称图
形吗?如果是,它有几条
对称轴?试着画出来,并
用对折的方法进行验证.
2.观察角有什么特征?
3.图中直角三角形有哪些?O合作探究动手操作
步骤:①将矩形的各个顶点,如图标上字母;
②连结矩形ABCD的对角线,交点为点O。ABCDO结论:①矩形是轴对称图形,有两条对称轴,对称轴为对边的中点的连线所在的直线。②矩形的四个内角都是直角。③图中直角三角形:Rt△ABC,Rt△BCD,Rt△CDA,
Rt△ABD
探究成果4.观察对角线之间有什么
数量关系?
5.图中相等的线段有哪些?
6.图中等腰三角形有哪些?O?????深入探究O探究成果5.相等的线段:
AB=CD,AD=BC, AC=BD,OA=OC=OB=OD;6.等腰三角形:
△AOB,△BOC,△COD,△AOD4.矩形的对角线相等; 比一比,填一填中心对称
图形对边平行
且相等对角相等
邻角互补互相平分
轴对称图形四个内角
都是直角相等证明:矩形的四个角都是直角ABCD证明:在矩形ABCD中,∵AD//BC(两直线平行,同旁内角互补)(已知)(等式的性质)(矩形的对角相等)(等量代换)(矩形的对边平行)矩形的性质定理1: 矩形的四个角都是直角∵四边形ABCD是矩形∴ ∠A=∠B = ∠C=∠D = 90°证明:矩形的对角线相等BADCO已知:在矩形ABCD中,对角线AC和BD相交于点O求证:AC=BD证明:∵四边形ABCD是矩形(已知)∴AB=CD(矩形的对边相等)
∠ABC=∠BCD = 90°(矩形的四个角是直角) ∵BC=CB(公共边)即AC=BD(全等三角形的对应边相等)矩形的性质定理2:矩形的对角线相等.∵四边形ABCD是矩形∴AC=BD 在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,
求AC= ,OB= ,10685小试牛刀矩形具有而一般平行四边形不具有的性质是( )
A对角线相等 B对边相等
C对角相等 D对角线互相平分A巩固新知解:又∵AC=BD=13cm(矩形的对角线相等) ∵△AOB、△BOC、△COD和△AOD四个小三角形的周长和为86 cm(已知)∴AB+BC+CD+DA
=86-2(AC+BD) =86-4×13
=34(cm)即矩形ABCD的周长等于34cm例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)
=86矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2 这节课你学到了什么? 还有什么困惑吗?我的收获知识的升华1.认真复习《矩形的性质》,完成学法大视野的相关练习题。
2.完成教科书P100练习题。跳一跳,够得着!已知:如图,在矩形ABCD中,M为BC的中点.
求证:(2)若要使∠AMD是直角,应添加什
么条件?(1)AM=DM.
谢谢大家!
