浙江省台州市2018-2019学年第二学期九年级数学中考复习卷(2)(word版无答案)
文档属性
| 名称 | 浙江省台州市2018-2019学年第二学期九年级数学中考复习卷(2)(word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 217.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-03 00:00:00 | ||
图片预览



文档简介
2019年九年级数学中考复习卷二次
选择题。
1.﹣2019的倒数是(?? )
A.2019
B./
C.﹣2019
D./
2.下列图形中,既是轴对称图形,又是中心对称图形的是(?? )
A./?
B./??
C./
D./
3.我国最大的领海是南海,总面积有3 500 000平方公里,将数3 500 000用科学记数法表示应为(?? )
A.3.5×106
B.3.5×107
C.35×105
D.0.35×108
4.下列计算,结果等于x5的是(?? )
A.x2+x3
B.x2?x3
C.x10÷x2
D.(x2)3
6.已知某正多边形的一个内角是140°,则这个正多边形的边数是(?? )
A.6
B.7
C.8
D.9
7.不等式组/的解集在数轴上表示正确的是(?? )
A./
B./??????
C./
D./
8.甲、乙两地今年2月份前5天的日平均气温如图所示,则下列描述错误的是(?? )
/
A.两地气温的平均数相同
B.甲地气温的众数是4 ℃
C.乙地气温的中位数是6 ℃
D.甲地气温相对比较稳定
9.?数学家阿尔-花拉子米在《对消与还原》指出:对消即将方程中各项成对消除,相当于现代解方程中的“合并同类项”;还原即把方程转换成左边各项都含有未知数,右边各项不含有未知数的形式,相当于现代解方程中的“移项”.右图解方程的步骤中属于“还原”的是(?? )
??????????/
A.①
B.②
C.③
D.④
10.设关于x的方程x2+px+q+1=0的两个实数根是m、n(mA.mB.mC.dD.d11. 某条公共汽车线路收支差额y与乘客量x的函数关系如图所示(收支差额=车票收入﹣支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则(?? )
/
A.①反映了建议(Ⅰ),③反映了建议(Ⅱ)
B.②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C.①反映了建议(Ⅱ),③反映了建议(Ⅰ)
D.②反映了建议(Ⅱ),④反映了建议(Ⅰ)
二.填空题
11.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛.
?????? 设共有x个队参加比赛,则依题意可列方程为??????????.
12.如图,∠MON的顶点在量角器的边缘上,且OM与量角器0刻度线重合,角的另一边ON与量角器边缘交点刻度为50,则∠MON=??????????.
?/
13.将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合,当α最小时,点A运动的路径长为??????????.
?/
14.已知x=y+8,则代数式x2﹣2xy+y2+36=?????? ???.
15.若数a使关于x的不等式组/有且只有4个整数解,且使关于y的分式方程/的解为正数,则符合条件的所有整数a的和为??????????.
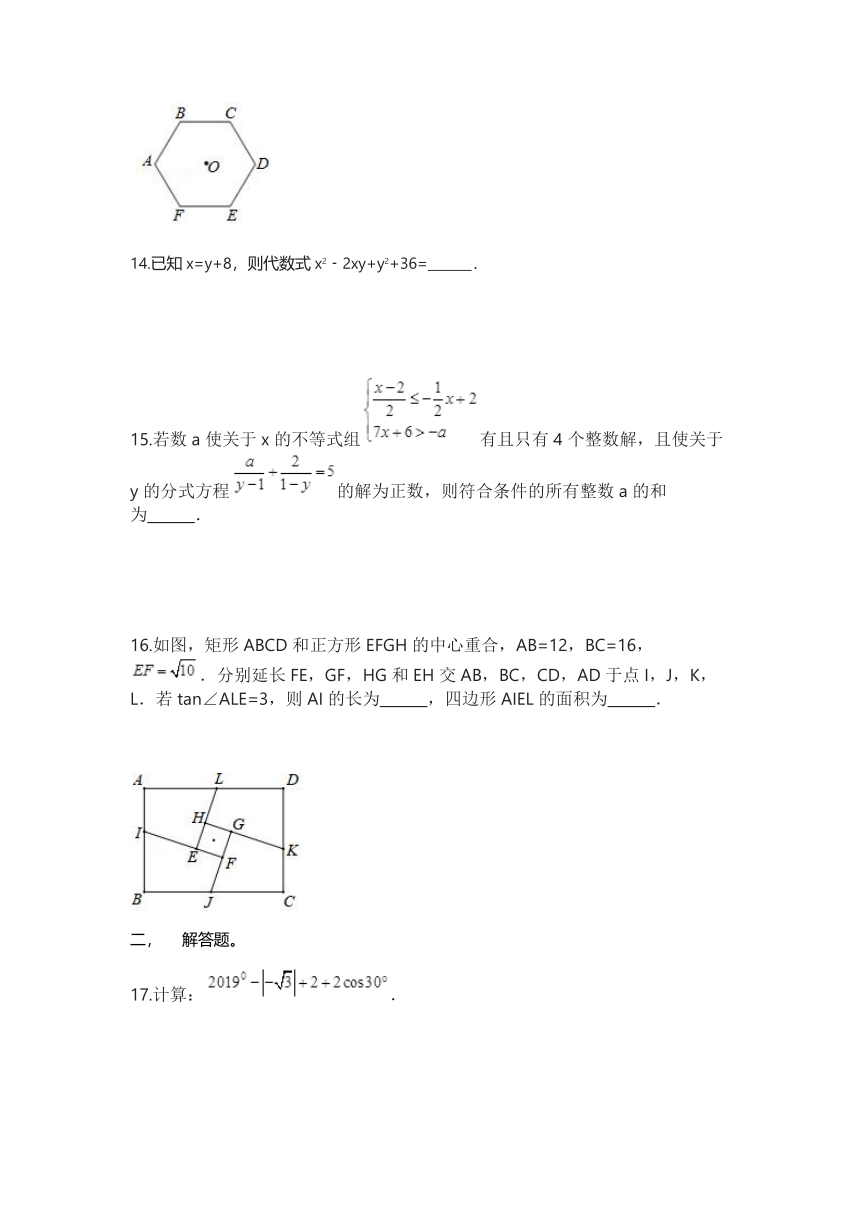
16.如图,矩形ABCD和正方形EFGH的中心重合,AB=12,BC=16,/.分别延长FE,GF,HG和EH交AB,BC,CD,AD于点I,J,K,L.若tan∠ALE=3,则AI的长为??????????,四边形AIEL的面积为??????????.
/
解答题。
17.计算:/.
18.先化简,再求值:/,其中a=3,b=1.
19.如图,5×5的正方形网格中隐去了一些网格线,AB,CD间的距离是2个单位,CD,EF间的距离是3个单位,格点O在CD上(网格线的交点叫格点).请分别在图①、②中作格点三角形OPQ,使得∠POQ=90°,其中点P在AB上,点Q在EF上,且它们不全等.
/
20.太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300 cm,AB的倾斜角为30°,BE=CA=50 cm,支撑角钢CD,EF与底座地基台面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30 cm,点A到地面的垂直距离为50 cm,求支撑角钢CD和EF的长度各是多少厘米(结果保留根号).
/
21.央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承﹣﹣地方戏曲进校园”的喜爱情况进行了随机调查.对收集的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
/
注:图中A表示“很喜欢”,B表示“喜欢”、C表示“一般”,D表示“不喜欢”.
?????? (1)被调查的总人数是??????????人,扇形统计图中C部分所对应的扇形圆心角的度数为??????????;
?????? (2)补全条形统计图;
?????? (3)若该校共有学生1 800人,请根据上述调查结果,估计该校学生中A类有??????????人;
?????? (4)在抽取的A类5人中,刚好有3个女生和2个男生,从中随机抽取两个同学担任两角色,用树状图或列表法求出被抽到的两个学生性别相同的概率.
/
22.已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转(在正方形内部),使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
/
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
(3)作点D关于AQ的对称点G,连接GM、GN,直接写出/的值.
23.我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为W万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;(写出自变量x的取值范围)
(2)求W与x之间的函数关系式;(写出自变量x的取值范围);并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
/
24.已知⊙O的半径为5,弦AB的长度为m,点C是弦AB所对优弧上的一
动点.
(1)如图①,若m=5,则∠C的度数为??????????°;
(2)如图②,若m=6.
①求∠C的正切值;
②若△ABC为等腰三角形,求△ABC面积.
/
选择题。
1.﹣2019的倒数是(?? )
A.2019
B./
C.﹣2019
D./
2.下列图形中,既是轴对称图形,又是中心对称图形的是(?? )
A./?
B./??
C./
D./
3.我国最大的领海是南海,总面积有3 500 000平方公里,将数3 500 000用科学记数法表示应为(?? )
A.3.5×106
B.3.5×107
C.35×105
D.0.35×108
4.下列计算,结果等于x5的是(?? )
A.x2+x3
B.x2?x3
C.x10÷x2
D.(x2)3
6.已知某正多边形的一个内角是140°,则这个正多边形的边数是(?? )
A.6
B.7
C.8
D.9
7.不等式组/的解集在数轴上表示正确的是(?? )
A./
B./??????
C./
D./
8.甲、乙两地今年2月份前5天的日平均气温如图所示,则下列描述错误的是(?? )
/
A.两地气温的平均数相同
B.甲地气温的众数是4 ℃
C.乙地气温的中位数是6 ℃
D.甲地气温相对比较稳定
9.?数学家阿尔-花拉子米在《对消与还原》指出:对消即将方程中各项成对消除,相当于现代解方程中的“合并同类项”;还原即把方程转换成左边各项都含有未知数,右边各项不含有未知数的形式,相当于现代解方程中的“移项”.右图解方程的步骤中属于“还原”的是(?? )
??????????/
A.①
B.②
C.③
D.④
10.设关于x的方程x2+px+q+1=0的两个实数根是m、n(m
/
A.①反映了建议(Ⅰ),③反映了建议(Ⅱ)
B.②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C.①反映了建议(Ⅱ),③反映了建议(Ⅰ)
D.②反映了建议(Ⅱ),④反映了建议(Ⅰ)
二.填空题
11.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛.
?????? 设共有x个队参加比赛,则依题意可列方程为??????????.
12.如图,∠MON的顶点在量角器的边缘上,且OM与量角器0刻度线重合,角的另一边ON与量角器边缘交点刻度为50,则∠MON=??????????.
?/
13.将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合,当α最小时,点A运动的路径长为??????????.
?/
14.已知x=y+8,则代数式x2﹣2xy+y2+36=?????? ???.
15.若数a使关于x的不等式组/有且只有4个整数解,且使关于y的分式方程/的解为正数,则符合条件的所有整数a的和为??????????.
16.如图,矩形ABCD和正方形EFGH的中心重合,AB=12,BC=16,/.分别延长FE,GF,HG和EH交AB,BC,CD,AD于点I,J,K,L.若tan∠ALE=3,则AI的长为??????????,四边形AIEL的面积为??????????.
/
解答题。
17.计算:/.
18.先化简,再求值:/,其中a=3,b=1.
19.如图,5×5的正方形网格中隐去了一些网格线,AB,CD间的距离是2个单位,CD,EF间的距离是3个单位,格点O在CD上(网格线的交点叫格点).请分别在图①、②中作格点三角形OPQ,使得∠POQ=90°,其中点P在AB上,点Q在EF上,且它们不全等.
/
20.太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300 cm,AB的倾斜角为30°,BE=CA=50 cm,支撑角钢CD,EF与底座地基台面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30 cm,点A到地面的垂直距离为50 cm,求支撑角钢CD和EF的长度各是多少厘米(结果保留根号).
/
21.央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承﹣﹣地方戏曲进校园”的喜爱情况进行了随机调查.对收集的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
/
注:图中A表示“很喜欢”,B表示“喜欢”、C表示“一般”,D表示“不喜欢”.
?????? (1)被调查的总人数是??????????人,扇形统计图中C部分所对应的扇形圆心角的度数为??????????;
?????? (2)补全条形统计图;
?????? (3)若该校共有学生1 800人,请根据上述调查结果,估计该校学生中A类有??????????人;
?????? (4)在抽取的A类5人中,刚好有3个女生和2个男生,从中随机抽取两个同学担任两角色,用树状图或列表法求出被抽到的两个学生性别相同的概率.
/
22.已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转(在正方形内部),使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
/
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
(3)作点D关于AQ的对称点G,连接GM、GN,直接写出/的值.
23.我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为W万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;(写出自变量x的取值范围)
(2)求W与x之间的函数关系式;(写出自变量x的取值范围);并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
/
24.已知⊙O的半径为5,弦AB的长度为m,点C是弦AB所对优弧上的一
动点.
(1)如图①,若m=5,则∠C的度数为??????????°;
(2)如图②,若m=6.
①求∠C的正切值;
②若△ABC为等腰三角形,求△ABC面积.
/
同课章节目录
