人教B版高中数学必修一 3.3幂函数课件 共22张PPT
文档属性
| 名称 | 人教B版高中数学必修一 3.3幂函数课件 共22张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 574.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 18:31:16 | ||
图片预览






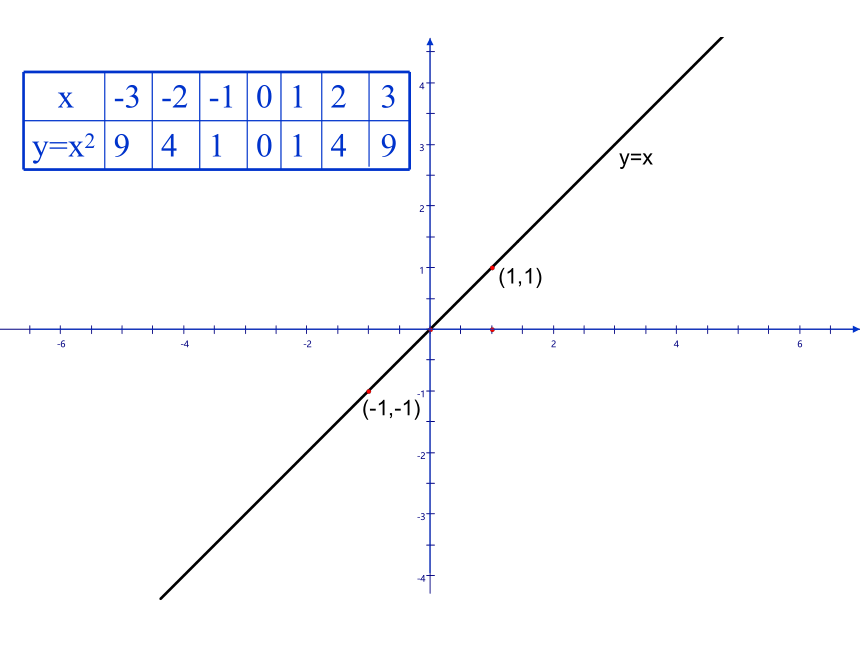

文档简介
课件22张PPT。3.3 幂函数1.明确幂函数的定义,会判断函数是不是幂函数:
2.根据具体函数的图象总结幂函数的性质,并能利用性质解决简单的幂函数问题。概念形成这些函数的表达式有什么共同的特征?这类函数表达式的一般形式应该如何表示?概念形成 一般地,形如
的函数称为幂函数(power fun_ction) ,
其中x为自变量, 为常数。练习1、判断下列函数中,哪些是幂函数?
(1)y =x-2 (2)y=2x2
(3) (4)y=2x
(5) y=x3 +2 (6)y=(x-1)3概念深化幂函数
有哪些性质?y=x-2
例1. 利用单调性判断下列各值的大小。(1)5.20.8 与 5.30.8
(2)0.20.3 与 0.30.3
(3) 解:(1)y= x0.8在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x0.3在(0,+∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3(3)y=x-1/2在(0,+∞)内是减函数
∵1.1>0.9∴ 1.1-1/2<0.9-1/2应用举例利用幂函数或指数函数比较大小关键在于构造出适当的函数。
1.若指数相同底数不同,考虑幂函数;如
2.若指数不同底数相同,考虑指数函数;
3.若底数指数都不同,经常要引入中间量。
如应用举例2. 观察 的值,确定幂函数在第一象限的大致走势。3. 描点(特殊点)、画图象。练习4:试作出幂函数 的图象。应用举例思考:如何做出幂函数的图象?1. 把幂函数化成根式,判断定义域、奇偶性。应用举例当堂检测归纳小结说说你的收获是什么?1.幂函数的概念;2.幂函数的图象和性质;
3.观察、归纳、类比是发现
数学问题的重要方法;
4.函数思想,数形结合思想。
华罗庚教授说过:
“数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事非.” 作业:必做题:课本110页A,1(1),2(3),
3, 4,B,1.选做题:课本110页B,3
2.根据具体函数的图象总结幂函数的性质,并能利用性质解决简单的幂函数问题。概念形成这些函数的表达式有什么共同的特征?这类函数表达式的一般形式应该如何表示?概念形成 一般地,形如
的函数称为幂函数(power fun_ction) ,
其中x为自变量, 为常数。练习1、判断下列函数中,哪些是幂函数?
(1)y =x-2 (2)y=2x2
(3) (4)y=2x
(5) y=x3 +2 (6)y=(x-1)3概念深化幂函数
有哪些性质?y=x-2
例1. 利用单调性判断下列各值的大小。(1)5.20.8 与 5.30.8
(2)0.20.3 与 0.30.3
(3) 解:(1)y= x0.8在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x0.3在(0,+∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3(3)y=x-1/2在(0,+∞)内是减函数
∵1.1>0.9∴ 1.1-1/2<0.9-1/2应用举例利用幂函数或指数函数比较大小关键在于构造出适当的函数。
1.若指数相同底数不同,考虑幂函数;如
2.若指数不同底数相同,考虑指数函数;
3.若底数指数都不同,经常要引入中间量。
如应用举例2. 观察 的值,确定幂函数在第一象限的大致走势。3. 描点(特殊点)、画图象。练习4:试作出幂函数 的图象。应用举例思考:如何做出幂函数的图象?1. 把幂函数化成根式,判断定义域、奇偶性。应用举例当堂检测归纳小结说说你的收获是什么?1.幂函数的概念;2.幂函数的图象和性质;
3.观察、归纳、类比是发现
数学问题的重要方法;
4.函数思想,数形结合思想。
华罗庚教授说过:
“数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事非.” 作业:必做题:课本110页A,1(1),2(3),
3, 4,B,1.选做题:课本110页B,3
