人教B版高中数学必修一3.2.1 对数的概念课件 共21张PPT
文档属性
| 名称 | 人教B版高中数学必修一3.2.1 对数的概念课件 共21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 335.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 18:32:34 | ||
图片预览




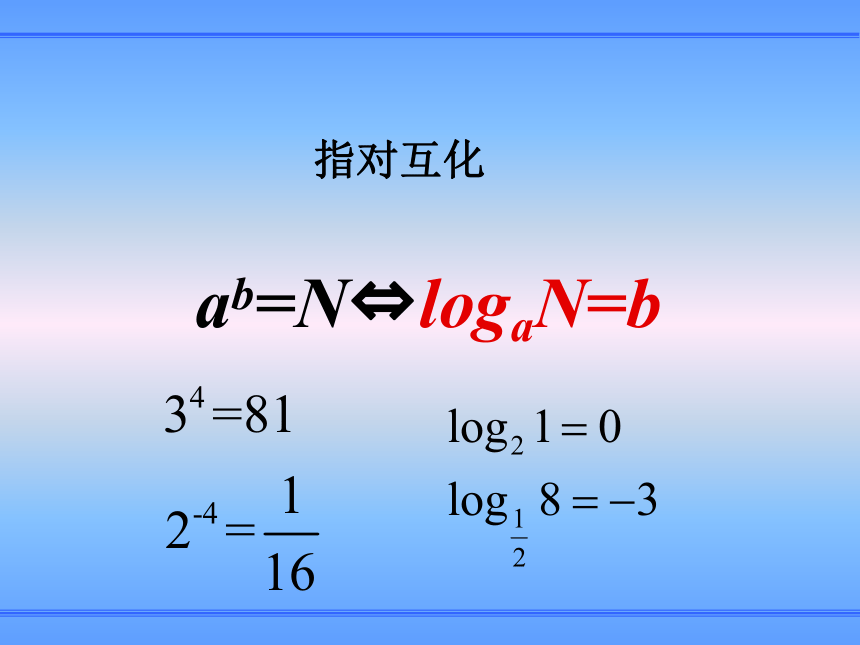


文档简介
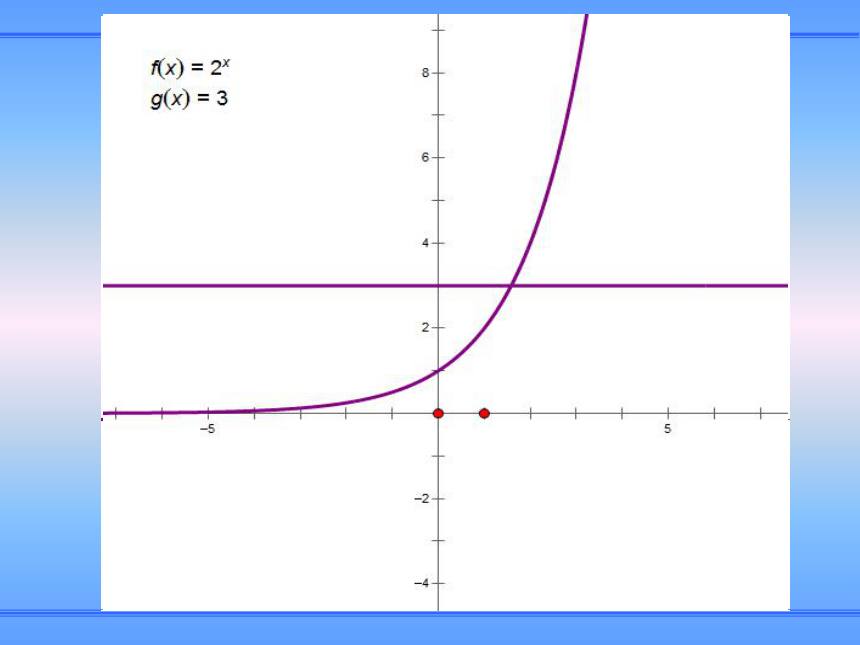
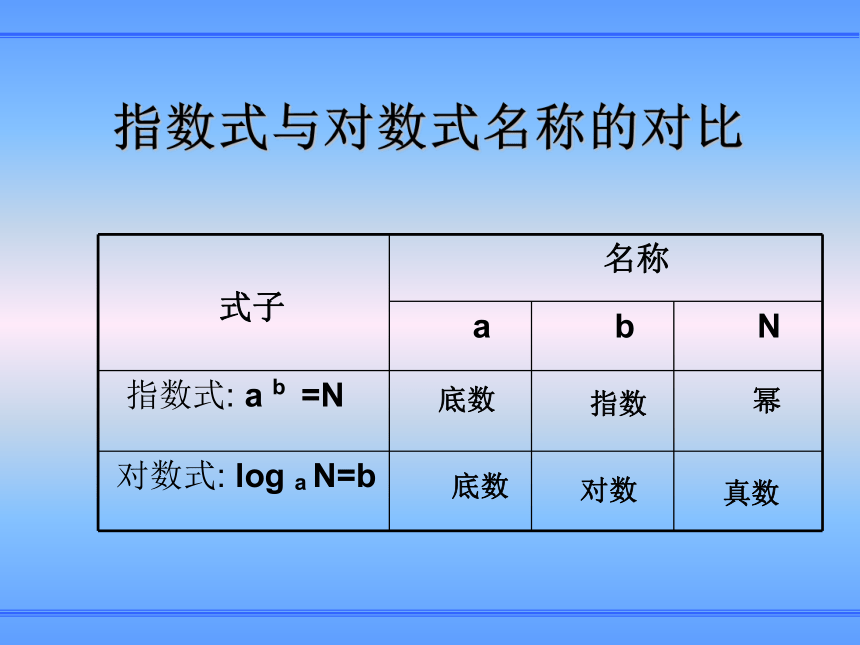
课件21张PPT。如果我们拿出一张纸对折,纸就变成了两层,再对折,就变成了四层,继续对折……你能提出怎样的问题?b存在吗?若存在有几个呢?你能否把b表示出来呢?读法:以a为底N的对数记法:定义:记作a叫做对数的底数,N叫做真数。指数式与对数式名称的对比底数
指数底数
对数
幂真数ab=N?logaN=b指对互化 对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年)。他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发现。纳皮尔与对数对数的文化意义恩格斯说,对数的发明与解析几何的创立、微积分的建立是17世纪数学史上的3大成就。伽利略说,给我空间、时间及对数,
我可以创造一个宇宙。
布里格斯(常用对数表的发明者)说,对数
的发明,延长了天文学家的寿命。 2014-10191/3探究内容:
对上面的练习,进行观察归纳,探究发现对数的性质并证明.
对数的性质(1)根据对数的定义求(2)负数与0有没有对数?负数与0有没有对数两式都成立说明:例1.把下列指数式化成对数式,把对数式化 成指数式练习课堂总结a b = Nb = log a N1.关系:2.特殊对数:1)常用对数 — 以10为底的对数;lg N
2)自然对数— 以 e 为底的对数;ln N3.对数恒等式:4.重要结论:1)log a a = 1;2)log a 1 = 0拓展提高2.计算2.计算
指数底数
对数
幂真数ab=N?logaN=b指对互化 对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年)。他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发现。纳皮尔与对数对数的文化意义恩格斯说,对数的发明与解析几何的创立、微积分的建立是17世纪数学史上的3大成就。伽利略说,给我空间、时间及对数,
我可以创造一个宇宙。
布里格斯(常用对数表的发明者)说,对数
的发明,延长了天文学家的寿命。 2014-10191/3探究内容:
对上面的练习,进行观察归纳,探究发现对数的性质并证明.
对数的性质(1)根据对数的定义求(2)负数与0有没有对数?负数与0有没有对数两式都成立说明:例1.把下列指数式化成对数式,把对数式化 成指数式练习课堂总结a b = Nb = log a N1.关系:2.特殊对数:1)常用对数 — 以10为底的对数;lg N
2)自然对数— 以 e 为底的对数;ln N3.对数恒等式:4.重要结论:1)log a a = 1;2)log a 1 = 0拓展提高2.计算2.计算
