人教B版高中数学必修一课件:3.3幂函数 共16张PPT
文档属性
| 名称 | 人教B版高中数学必修一课件:3.3幂函数 共16张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 734.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 18:33:45 | ||
图片预览






文档简介
课件16张PPT。一.学习目标: 3.3幂函数1.通过实例,了解幂函数的概念、图象和性质,会应用幂函数的图象与性质比较数或代数式的大小.
2.通过幂函数图象的学习,加深对幂函数性质的理解,体会通过观察、分析函数图象来研究函数性质的方法.1:如果李阿姨购买了价格为1元的桑椹干包装盒x个,
那么她支付的钱数 (元)
2:如果一个正方形的桑椹园边长为x米,那么桑椹园的 面积 (平方米)
夏津人杰地灵,物阜民丰。夏津的桑椹更是闻名遐迩。请同学们阅读以下材料并思考问题:x 创设情境,导入课题:3:如果正方体的桑椹干包装盒棱长为x厘米,那么包装盒的体积 .(立方厘米)
4:如果正方形桑椹园的面积为x平方米,那么桑椹园的
边长 (米)
5:如果李阿姨去买桑椹干,经过x秒骑车行进了1千米,那么她骑车的平均速度 这些函数解析式从形式上有什么共同特征?我们把具有这种形式的函数叫做幂函数.函数解析式都是幂的形式:
(1) 底数为自变量;
(2) 指数为常数;
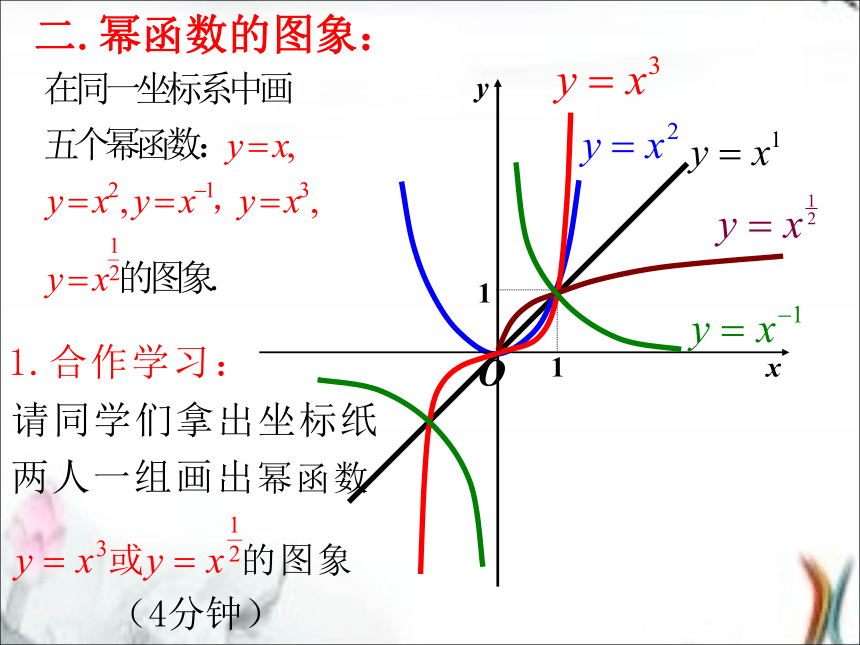
(3) 幂的系数为1.一.幂函数的概念.一试身手1:(3) ( ) ( ) ×??(1) y=x4 ( )( )( )(5) (6) ?( )××判断下列函数是否为幂函数:注意:在幂函数当中,指数 可以是正数,负数,也可为零,即二.幂函数的图象: (4分钟)小组合作探究三.幂函数的性质 问题1:观察图象,在
第一象限内你能发现函
数的指数与图象的位置
有什么关系吗?问题2:幂函数图象的
分布有何规律?它们
又有何共性(3分钟)X yOy=x-1y=x2y=x3y=xy=xx=1三.幂函数的性质 问题一:观察图象,在
第一象限内你能发现函
数的指数与图象的位置
有什么关系吗?发现一:一般地,幂函数的图象在y轴和直线x=1之间时,指数越大,图象越低,指数越小,图象越高;而在直线
x=1右侧,情况正好相反。一试身手2: 如图所示,曲线是幂函数 y = xk 在第一象限内的图象,已知 k分别取 四个值,则相应图象依次为:________ . 1X yOy=x-1y=x2y=x3y=xy=xx=1再观察这五个函数图象,幂函数还具有什么性质?三.幂函数的性质 X y110y110α> 0α< 0 (1)图象都过(0,0)点
(2)在第一象限内,函数值随x 的增大而增大,函数即在[0,+∞)上是增函数。 (1)图象都不过(0,0)点;
(2)在第一象限内,函数值随x 的增大而减小,即函数在(0,+∞)上是减函数。
(3)在第一象限内,函数图象向右无限靠近x轴,向上无限趋近于y轴。思考:反之成立吗?发现三 例1:比较下列各组数中两个数的大小.四:学以致用五:我的收获基本初等函数(一)幂函数定义性质对数函数指数函数分类讨论
数形结合图象六:达标检测:m=-3一四1.设 函数 的图象必过第 象限,不过第 象限。 谢谢聆听,欢迎指导!
2.通过幂函数图象的学习,加深对幂函数性质的理解,体会通过观察、分析函数图象来研究函数性质的方法.1:如果李阿姨购买了价格为1元的桑椹干包装盒x个,
那么她支付的钱数 (元)
2:如果一个正方形的桑椹园边长为x米,那么桑椹园的 面积 (平方米)
夏津人杰地灵,物阜民丰。夏津的桑椹更是闻名遐迩。请同学们阅读以下材料并思考问题:x 创设情境,导入课题:3:如果正方体的桑椹干包装盒棱长为x厘米,那么包装盒的体积 .(立方厘米)
4:如果正方形桑椹园的面积为x平方米,那么桑椹园的
边长 (米)
5:如果李阿姨去买桑椹干,经过x秒骑车行进了1千米,那么她骑车的平均速度 这些函数解析式从形式上有什么共同特征?我们把具有这种形式的函数叫做幂函数.函数解析式都是幂的形式:
(1) 底数为自变量;
(2) 指数为常数;
(3) 幂的系数为1.一.幂函数的概念.一试身手1:(3) ( ) ( ) ×??(1) y=x4 ( )( )( )(5) (6) ?( )××判断下列函数是否为幂函数:注意:在幂函数当中,指数 可以是正数,负数,也可为零,即二.幂函数的图象: (4分钟)小组合作探究三.幂函数的性质 问题1:观察图象,在
第一象限内你能发现函
数的指数与图象的位置
有什么关系吗?问题2:幂函数图象的
分布有何规律?它们
又有何共性(3分钟)X yOy=x-1y=x2y=x3y=xy=xx=1三.幂函数的性质 问题一:观察图象,在
第一象限内你能发现函
数的指数与图象的位置
有什么关系吗?发现一:一般地,幂函数的图象在y轴和直线x=1之间时,指数越大,图象越低,指数越小,图象越高;而在直线
x=1右侧,情况正好相反。一试身手2: 如图所示,曲线是幂函数 y = xk 在第一象限内的图象,已知 k分别取 四个值,则相应图象依次为:________ . 1X yOy=x-1y=x2y=x3y=xy=xx=1再观察这五个函数图象,幂函数还具有什么性质?三.幂函数的性质 X y110y110α> 0α< 0 (1)图象都过(0,0)点
(2)在第一象限内,函数值随x 的增大而增大,函数即在[0,+∞)上是增函数。 (1)图象都不过(0,0)点;
(2)在第一象限内,函数值随x 的增大而减小,即函数在(0,+∞)上是减函数。
(3)在第一象限内,函数图象向右无限靠近x轴,向上无限趋近于y轴。思考:反之成立吗?发现三 例1:比较下列各组数中两个数的大小.四:学以致用五:我的收获基本初等函数(一)幂函数定义性质对数函数指数函数分类讨论
数形结合图象六:达标检测:m=-3一四1.设 函数 的图象必过第 象限,不过第 象限。 谢谢聆听,欢迎指导!
