人教B版高中数学选修2-1 2.2.1《椭圆的标准方程》课件 共19张PPT
文档属性
| 名称 | 人教B版高中数学选修2-1 2.2.1《椭圆的标准方程》课件 共19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 18:35:00 | ||
图片预览





文档简介
课件19张PPT。2.2.1《椭圆的标准方程》
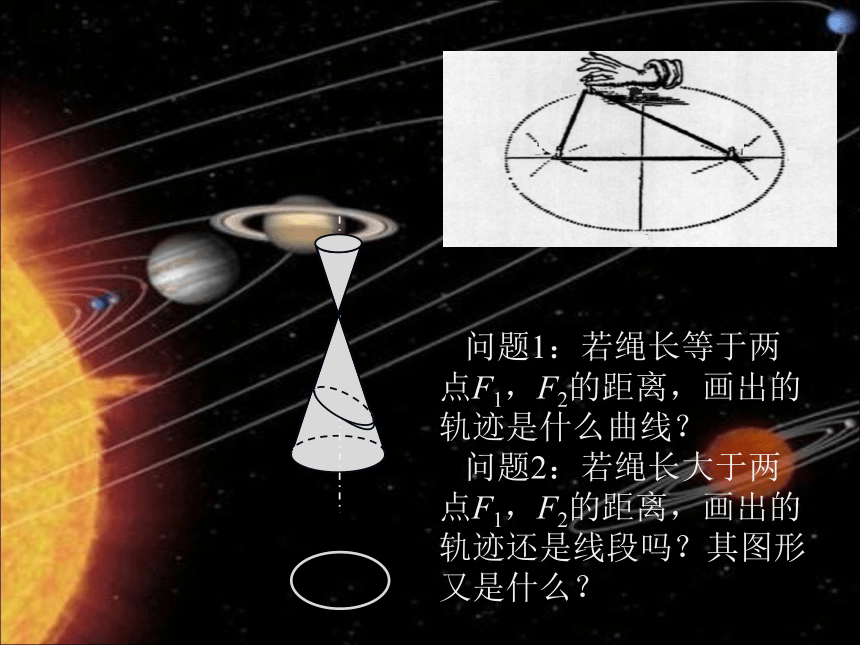
问题1:若绳长等于两点F1,F2的距离,画出的轨迹是什么曲线?
问题2:若绳长大于两点F1,F2的距离,画出的轨迹还是线段吗?其图形又是什么?定义中的条件2a>|F1F2|>0不能少,这是根据三角形中的两边之和大于第三边得出来的.否则:
(1)当2a=|F1F2|时,其轨迹为线段F1F2;
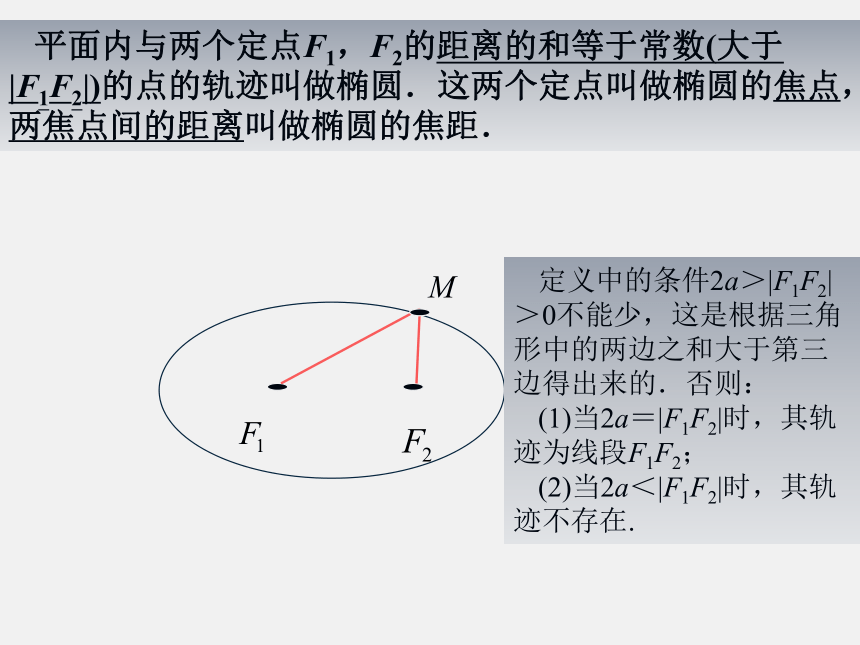
(2)当2a<|F1F2|时,其轨迹不存在.平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.上式两边再平方,得整理得 1.标准方程的几何特征:椭圆的中心在坐标原点,焦点在x轴或y轴上,对称轴是坐标轴.
2.标准方程的代数特征:方程右边是1,左边是关于x,y的平方和,并且分母不相等.
3.a,b,c三个量的关系:椭圆的标准方程中,a2 =c2+b2[例1]已知椭圆 的焦点在y轴上,若焦距为4,则m的值?解:由题意得m-2>10-m>0,
解得6<m<10.
又a2=m-2,b2=10-m,
则c2=a2-b2=2m-12=4,
解得m=8.
[例2] 求满足下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-4,0)和(4,0),且椭圆经过点(5,0);
(2)焦点在y轴上,且经过两个点(0,2)和(1,0).[例3]已知 两个定点, 且 的周长等于18,求这个三角形的顶点 的轨迹方程。特别注意:这是个三角形所以最后方程要考虑实际问题。 [达标检测]课堂总结求解椭圆方程方法:定义法,待定系数法数学思想:数形结合思想;转化化归思想;分类讨论思想;方程的思想。作业布置①课本42页练习A B组
②查找资料完成椭圆不同画法和历史。
问题2:若绳长大于两点F1,F2的距离,画出的轨迹还是线段吗?其图形又是什么?定义中的条件2a>|F1F2|>0不能少,这是根据三角形中的两边之和大于第三边得出来的.否则:
(1)当2a=|F1F2|时,其轨迹为线段F1F2;
(2)当2a<|F1F2|时,其轨迹不存在.平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.上式两边再平方,得整理得 1.标准方程的几何特征:椭圆的中心在坐标原点,焦点在x轴或y轴上,对称轴是坐标轴.
2.标准方程的代数特征:方程右边是1,左边是关于x,y的平方和,并且分母不相等.
3.a,b,c三个量的关系:椭圆的标准方程中,a2 =c2+b2[例1]已知椭圆 的焦点在y轴上,若焦距为4,则m的值?解:由题意得m-2>10-m>0,
解得6<m<10.
又a2=m-2,b2=10-m,
则c2=a2-b2=2m-12=4,
解得m=8.
[例2] 求满足下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-4,0)和(4,0),且椭圆经过点(5,0);
(2)焦点在y轴上,且经过两个点(0,2)和(1,0).[例3]已知 两个定点, 且 的周长等于18,求这个三角形的顶点 的轨迹方程。特别注意:这是个三角形所以最后方程要考虑实际问题。 [达标检测]课堂总结求解椭圆方程方法:定义法,待定系数法数学思想:数形结合思想;转化化归思想;分类讨论思想;方程的思想。作业布置①课本42页练习A B组
②查找资料完成椭圆不同画法和历史。
