人教版高中数学选修2-3 1.2.2组合 课件(共14张PPT)
文档属性
| 名称 | 人教版高中数学选修2-3 1.2.2组合 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 121.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 18:37:56 | ||
图片预览




文档简介
课件14张PPT。1.2.2组合(一)学习目标:
1.理解组合的意义,能判断一个问题是排列问题还是组合问题
2.了解组合数的意义,会利用排列与组合的关系推导组合数公式
3. 能运用组合数公式进行简单计算
和证明
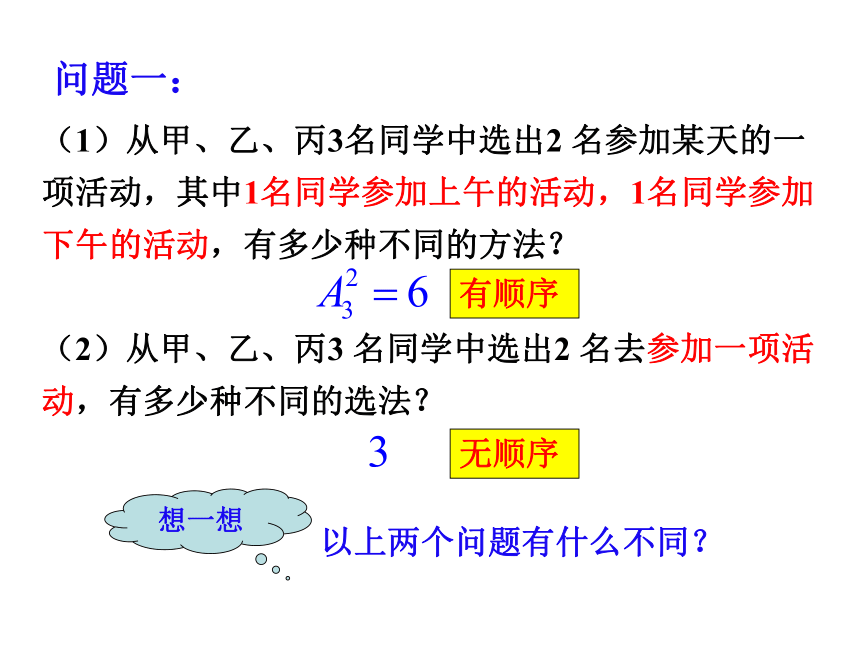
学习重点:组合的概念、组合数公式和性质学习难点:组合数公式的推导问题一:(1)从甲、乙、丙3名同学中选出2 名参加某天的一
项活动,其中1名同学参加上午的活动,1名同学参加
下午的活动,有多少种不同的方法?
(2)从甲、乙、丙3 名同学中选出2 名去参加一项活
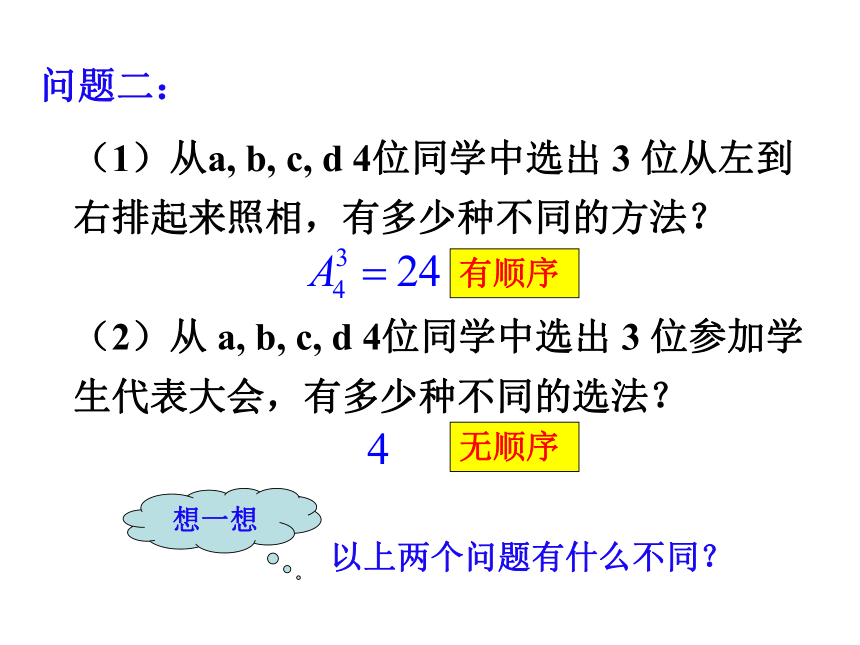
动,有多少种不同的选法?想一想以上两个问题有什么不同?有顺序无顺序问题二:(1)从a, b, c, d 4位同学中选出 3 位从左到右排起来照相,有多少种不同的方法?
(2)从 a, b, c, d 4位同学中选出 3 位参加学生代表大会,有多少种不同的选法?想一想以上两个问题有什么不同?有顺序无顺序思考1:排列与组合的概念有什么共同点、不同点? 两者都要“从n个不同元素中任取m个元素”;但排列与元素的顺序有关,组合与顺序无关。两个相同的排列有什么特点?两个相同的组合呢?思考2: 一般地,从n个不同元素中取出m(m≤n)
个元素并成一组,叫做从n个不同元素中取出
m个元素的一个组合.组合的定义:例1、判断下列问题是排列问题,还是组合问题,
并求出相应的排列数或组合数。
(1)10个人相互写一封信(由寄信人和收信人)
(2)10个人约定用手机相互通一次电话
(3)10个人以单循环进行象棋比赛(每人与其他选手
各比赛一场)
(4)10个人以单循环进行象棋比赛,冠亚军获得者有
多少种可能?
(5)从10个人里选出两个同学去打饭,共有多少种选法?
(6)从10个人里选出两个同学分别去打饭和打菜
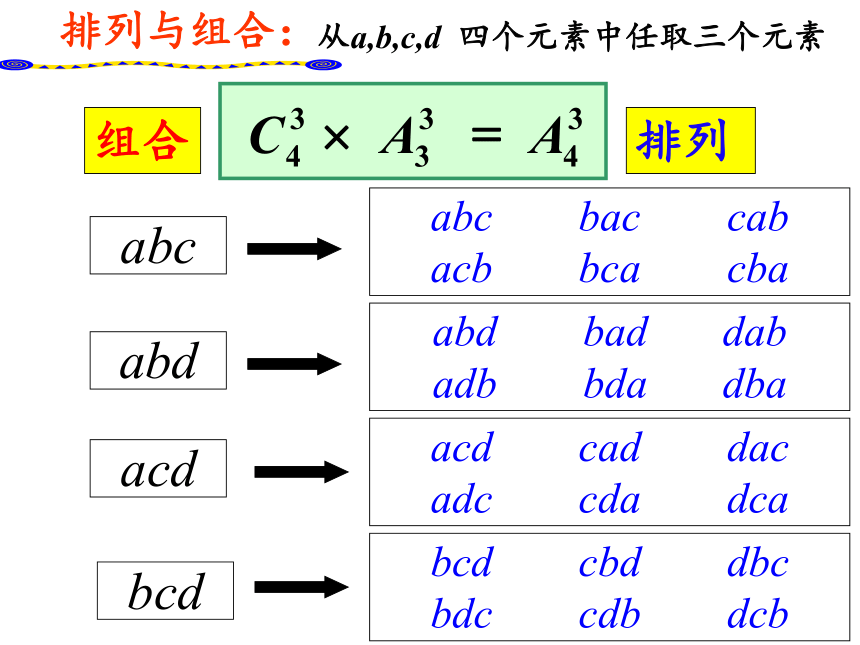
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.如:从 a , b , c三个不同的元素中取出两个元素的所有组合分别是:ab , ac , bc 思考:组合数定义:从a,b,c,d 四个元素中任取三个元素排列与组合:组合排列abcabdacdbcdabc bac cab
acb bca cbaabd bad dab
adb bda dbaacd cad dac
adc cda dcabcd cbd dbc
bdc cdb dcb从n 个不同元中取出m个元素的排列数 规定:组合数公式:例2、学院附中2010年有8个班级分别组建了8支足球队,
参加学校举行的单循环赛:
(1)共需比赛多少场?
(2)冠亚军共有多少种可能?变式、学院附中在2012年举办了一次以班级为单位的
足球赛,比赛采用单循环赛的方式(每支队伍
都要和其他队伍各比赛一场),一共进行了45
场比赛,问:共有多少支队伍参加比赛。例3、计算:(1)(2)例4、求证:例5、计算:1、写出从 5个元素 a,b,c,d,e 中任取 3个元素的所有组合。2、计算:3、求证:15148巩固练习课堂小结:1、通过本节课的学习,要求理解组合的概念,掌握
组合数公式并会运用解决一些简单的问题。2、注意搞清排列与组合的联系与区别,这是学好本节
课的关键。布置作业选修2-3作业本P10-P11
A组1-12、14、15、16
B组1-10、14
1.理解组合的意义,能判断一个问题是排列问题还是组合问题
2.了解组合数的意义,会利用排列与组合的关系推导组合数公式
3. 能运用组合数公式进行简单计算
和证明
学习重点:组合的概念、组合数公式和性质学习难点:组合数公式的推导问题一:(1)从甲、乙、丙3名同学中选出2 名参加某天的一
项活动,其中1名同学参加上午的活动,1名同学参加
下午的活动,有多少种不同的方法?
(2)从甲、乙、丙3 名同学中选出2 名去参加一项活
动,有多少种不同的选法?想一想以上两个问题有什么不同?有顺序无顺序问题二:(1)从a, b, c, d 4位同学中选出 3 位从左到右排起来照相,有多少种不同的方法?
(2)从 a, b, c, d 4位同学中选出 3 位参加学生代表大会,有多少种不同的选法?想一想以上两个问题有什么不同?有顺序无顺序思考1:排列与组合的概念有什么共同点、不同点? 两者都要“从n个不同元素中任取m个元素”;但排列与元素的顺序有关,组合与顺序无关。两个相同的排列有什么特点?两个相同的组合呢?思考2: 一般地,从n个不同元素中取出m(m≤n)
个元素并成一组,叫做从n个不同元素中取出
m个元素的一个组合.组合的定义:例1、判断下列问题是排列问题,还是组合问题,
并求出相应的排列数或组合数。
(1)10个人相互写一封信(由寄信人和收信人)
(2)10个人约定用手机相互通一次电话
(3)10个人以单循环进行象棋比赛(每人与其他选手
各比赛一场)
(4)10个人以单循环进行象棋比赛,冠亚军获得者有
多少种可能?
(5)从10个人里选出两个同学去打饭,共有多少种选法?
(6)从10个人里选出两个同学分别去打饭和打菜
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.如:从 a , b , c三个不同的元素中取出两个元素的所有组合分别是:ab , ac , bc 思考:组合数定义:从a,b,c,d 四个元素中任取三个元素排列与组合:组合排列abcabdacdbcdabc bac cab
acb bca cbaabd bad dab
adb bda dbaacd cad dac
adc cda dcabcd cbd dbc
bdc cdb dcb从n 个不同元中取出m个元素的排列数 规定:组合数公式:例2、学院附中2010年有8个班级分别组建了8支足球队,
参加学校举行的单循环赛:
(1)共需比赛多少场?
(2)冠亚军共有多少种可能?变式、学院附中在2012年举办了一次以班级为单位的
足球赛,比赛采用单循环赛的方式(每支队伍
都要和其他队伍各比赛一场),一共进行了45
场比赛,问:共有多少支队伍参加比赛。例3、计算:(1)(2)例4、求证:例5、计算:1、写出从 5个元素 a,b,c,d,e 中任取 3个元素的所有组合。2、计算:3、求证:15148巩固练习课堂小结:1、通过本节课的学习,要求理解组合的概念,掌握
组合数公式并会运用解决一些简单的问题。2、注意搞清排列与组合的联系与区别,这是学好本节
课的关键。布置作业选修2-3作业本P10-P11
A组1-12、14、15、16
B组1-10、14
