冀教版九年级数学下册第30章二次函数单元检测试卷(有答案)
文档属性
| 名称 | 冀教版九年级数学下册第30章二次函数单元检测试卷(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 83.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 00:00:00 | ||
图片预览



文档简介
冀教版九年级数学下册
第30章 二次函数 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.下列函数中,是二次函数的是( )
A. B.
C. D.
?2.已知二次函数的图象如图,则下列结论中正确的是( )
A. B.
C. D.
?3.下列为四个二次函数的图形,哪一个函数在时有最大值
A. B.
C. D.
?4.已知抛物线(为常数),,,是抛物线上三点,则,,由小到大依序排列为( )
A. B.
C. D.
?
5.已知二次函数,当自变量取时的函数值小于,那么当自变量取时的函数值( )
A.小于 B.大于
C.等于 D.与的大小关系不确定
?6.二次函数,,是常数,且中的与的部分对应值如下表所示,则下列结论中,正确的个数有( )
;当时,;当时,的值随值的增大而减小;方程有两个不相等的实数根.
A.个 B.个 C.个 D.个
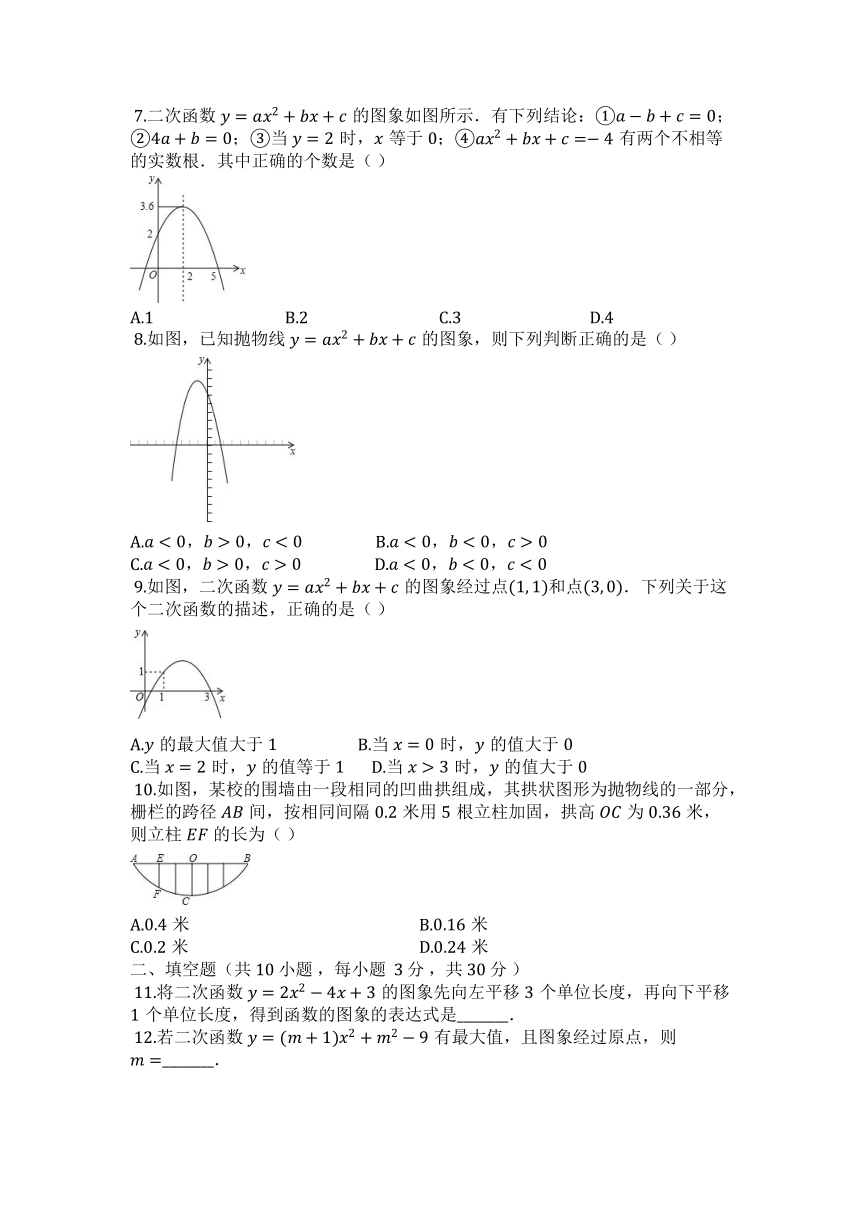
?7.二次函数的图象如图所示.有下列结论:①;②;③当时,等于;④有两个不相等的实数根.其中正确的个数是( )
A. B. C. D.
?8.如图,已知抛物线的图象,则下列判断正确的是( )
A.,, B.,,
C.,, D.,,
?9.如图,二次函数的图象经过点和点.下列关于这个二次函数的描述,正确的是( )
A.的最大值大于 B.当时,的值大于
C.当时,的值等于 D.当时,的值大于
?10.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径间,按相同间隔米用根立柱加固,拱高为米,则立柱的长为( )
A.米 B.米
C.米 D.米
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.将二次函数的图象先向左平移个单位长度,再向下平移个单位长度,得到函数的图象的表达式是________.
?12.若二次函数有最大值,且图象经过原点,则________.
?
13.已知二次函数与一次函数的图象交点为,,且二次函数的最小值为,则这个二次函数的解析式为________.
?14.我们把一元二次方程的解看成是抛物线与轴的交点的横坐标,如果把方程适当地变形,那么方程的解还可以看成是函数________与函数________的图象交点的横坐标(写出其中的一对).
?15.请选择一组你喜欢的、、的值,使二次函数的图象同时满足下列条件:①开口向下,②对称轴是直线;③顶点在轴下方,这样的二次函数的解析式可以是________.
?16.如图,抛物线与双曲线的交点的横坐标是,则关于的不等式的解集是________.
?
17.把函数化为的形式为________,此函数图象的对称轴是________,顶点坐标是________.
?18.正方形边长为,若边长增加,那么面积增加,则与的函数关系式是________.
?19.在同一坐标系中,函数,,的图象具有的共同特征是________.
?20.将进货为元的某种商品按元一个售出时,能卖出个,已知这时商品每涨价一元,其销售数就要减少个,为了获得最大利益,售价应定为________元.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.求下列函数的图象的对称轴、顶点坐标及与轴的交点坐标.
; ;
; .
?
22.已知一次函数的图象上有两点、,它们的横坐标分别是,,若二次函数的图象经过、两点.
请求出一次函数的表达式;
设二次函数的顶点为,求的面积.
?
23.某商场销售一种进价为元/台的台灯,经调查发现,该台灯每天的销售量(台),销售单价(元)满足,设销售这种台灯每天的利润为(元).
求与之间的函数关系式;
当销售单价定为多少元时.毎天的利润最大?最大利润多少?
在保证销售量尽可能大的前提下.该商场每天还想获得元的利润,应将销售单价定位为多少元?
?
24.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长的篱笆围成一个矩形花园(篱笆只围,两边),设?.
若花园的面积为,求的值;
若在处有一棵树与墙,的距离分别是和,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.
?
25.某企业设计了一款工艺品,每件的成本是元,为了合理定价,投放市场进行试销.据市场调查,销售单价是元时,每天的销售量是件,而销售单价每降低元,每天就可多售出件,但要求销售单价不得低于成本
求每天的销售利润(元)与销售单价(元)之间的函数关系式;
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
?
26.如图,已知二次函数的图象过,两点.
求这个二次函数的解析式;
设该二次函数的对称轴与轴交于点,连结,,求的面积;
求点和点所在直线的解析式,并根据图象求出当为何值时,.
答案
1.A
2.D
3.A
4.C
5.B
6.B
7.C
8.B
9.A
10.C
11.或
12.
13.或
14.
15.(不唯一)
16.
17.
18.
19.开口都向上,开口大小一样
20.
21.解:∵,
∴对称轴是直线,顶点坐标是,
解方程,
得,,
故它与轴交点坐标是,;∵,
∴对称轴是直线,顶点坐标是,
解方程,
得,
故它与轴的交点坐标是;∵,
∴对称轴是直线,顶点坐标是,
解方程,无解,
故它与轴没有交点;∵,
∴对称轴是直线,顶点坐标是,
当时,,
∴,
∴它与轴的交点坐标是.
22.解:设点坐标为;点坐标为.
∵、两点在的图象上,
∴,
.
∴,.
∵、两点又在的图象上,
∴.
解得.
∴一次函数的表达式是.
如下图,
设直线与轴的交点为,则点坐标为.
∴.
.
23.解:,
;∵,
,
∴当元时,最大利润元;由题意,,
即:,
解得:,,
又销售量随单价的增大而减小,
所以当时,既能保证销售量大,又可以每天获得元的利润.
24.解:由题意,得
,
∴当时,,
解得,,,
即花园的面积为,的值是或;由题意,
解得,,
∵花园面积
∴时,随的增大而增大.
∴当时,花园的面积取得最大值,
,
即在处有一棵树与墙,的距离分别是和,要将这棵树围在花园内(含边界,不考虑树的粗细),花园面积的最大值是.
25.解:
所以;
∵,
∴抛物线开口向下.
∵,对称轴是直线,
∴当时,;
即销售单价为元时,每天的销售利润最大,最大利润是元.
26.解:∵二次函数的图象过,两点,
∴,
解得:,
∴这个二次函数的解析式为:;抛物线的对称轴为:,
∴,
∴,
∴;设,
∴,
∴,
∴,
联立:,
解得:或,
∴当或时,.
第30章 二次函数 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.下列函数中,是二次函数的是( )
A. B.
C. D.
?2.已知二次函数的图象如图,则下列结论中正确的是( )
A. B.
C. D.
?3.下列为四个二次函数的图形,哪一个函数在时有最大值
A. B.
C. D.
?4.已知抛物线(为常数),,,是抛物线上三点,则,,由小到大依序排列为( )
A. B.
C. D.
?
5.已知二次函数,当自变量取时的函数值小于,那么当自变量取时的函数值( )
A.小于 B.大于
C.等于 D.与的大小关系不确定
?6.二次函数,,是常数,且中的与的部分对应值如下表所示,则下列结论中,正确的个数有( )
;当时,;当时,的值随值的增大而减小;方程有两个不相等的实数根.
A.个 B.个 C.个 D.个
?7.二次函数的图象如图所示.有下列结论:①;②;③当时,等于;④有两个不相等的实数根.其中正确的个数是( )
A. B. C. D.
?8.如图,已知抛物线的图象,则下列判断正确的是( )
A.,, B.,,
C.,, D.,,
?9.如图,二次函数的图象经过点和点.下列关于这个二次函数的描述,正确的是( )
A.的最大值大于 B.当时,的值大于
C.当时,的值等于 D.当时,的值大于
?10.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径间,按相同间隔米用根立柱加固,拱高为米,则立柱的长为( )
A.米 B.米
C.米 D.米
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.将二次函数的图象先向左平移个单位长度,再向下平移个单位长度,得到函数的图象的表达式是________.
?12.若二次函数有最大值,且图象经过原点,则________.
?
13.已知二次函数与一次函数的图象交点为,,且二次函数的最小值为,则这个二次函数的解析式为________.
?14.我们把一元二次方程的解看成是抛物线与轴的交点的横坐标,如果把方程适当地变形,那么方程的解还可以看成是函数________与函数________的图象交点的横坐标(写出其中的一对).
?15.请选择一组你喜欢的、、的值,使二次函数的图象同时满足下列条件:①开口向下,②对称轴是直线;③顶点在轴下方,这样的二次函数的解析式可以是________.
?16.如图,抛物线与双曲线的交点的横坐标是,则关于的不等式的解集是________.
?
17.把函数化为的形式为________,此函数图象的对称轴是________,顶点坐标是________.
?18.正方形边长为,若边长增加,那么面积增加,则与的函数关系式是________.
?19.在同一坐标系中,函数,,的图象具有的共同特征是________.
?20.将进货为元的某种商品按元一个售出时,能卖出个,已知这时商品每涨价一元,其销售数就要减少个,为了获得最大利益,售价应定为________元.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.求下列函数的图象的对称轴、顶点坐标及与轴的交点坐标.
; ;
; .
?
22.已知一次函数的图象上有两点、,它们的横坐标分别是,,若二次函数的图象经过、两点.
请求出一次函数的表达式;
设二次函数的顶点为,求的面积.
?
23.某商场销售一种进价为元/台的台灯,经调查发现,该台灯每天的销售量(台),销售单价(元)满足,设销售这种台灯每天的利润为(元).
求与之间的函数关系式;
当销售单价定为多少元时.毎天的利润最大?最大利润多少?
在保证销售量尽可能大的前提下.该商场每天还想获得元的利润,应将销售单价定位为多少元?
?
24.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长的篱笆围成一个矩形花园(篱笆只围,两边),设?.
若花园的面积为,求的值;
若在处有一棵树与墙,的距离分别是和,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.
?
25.某企业设计了一款工艺品,每件的成本是元,为了合理定价,投放市场进行试销.据市场调查,销售单价是元时,每天的销售量是件,而销售单价每降低元,每天就可多售出件,但要求销售单价不得低于成本
求每天的销售利润(元)与销售单价(元)之间的函数关系式;
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
?
26.如图,已知二次函数的图象过,两点.
求这个二次函数的解析式;
设该二次函数的对称轴与轴交于点,连结,,求的面积;
求点和点所在直线的解析式,并根据图象求出当为何值时,.
答案
1.A
2.D
3.A
4.C
5.B
6.B
7.C
8.B
9.A
10.C
11.或
12.
13.或
14.
15.(不唯一)
16.
17.
18.
19.开口都向上,开口大小一样
20.
21.解:∵,
∴对称轴是直线,顶点坐标是,
解方程,
得,,
故它与轴交点坐标是,;∵,
∴对称轴是直线,顶点坐标是,
解方程,
得,
故它与轴的交点坐标是;∵,
∴对称轴是直线,顶点坐标是,
解方程,无解,
故它与轴没有交点;∵,
∴对称轴是直线,顶点坐标是,
当时,,
∴,
∴它与轴的交点坐标是.
22.解:设点坐标为;点坐标为.
∵、两点在的图象上,
∴,
.
∴,.
∵、两点又在的图象上,
∴.
解得.
∴一次函数的表达式是.
如下图,
设直线与轴的交点为,则点坐标为.
∴.
.
23.解:,
;∵,
,
∴当元时,最大利润元;由题意,,
即:,
解得:,,
又销售量随单价的增大而减小,
所以当时,既能保证销售量大,又可以每天获得元的利润.
24.解:由题意,得
,
∴当时,,
解得,,,
即花园的面积为,的值是或;由题意,
解得,,
∵花园面积
∴时,随的增大而增大.
∴当时,花园的面积取得最大值,
,
即在处有一棵树与墙,的距离分别是和,要将这棵树围在花园内(含边界,不考虑树的粗细),花园面积的最大值是.
25.解:
所以;
∵,
∴抛物线开口向下.
∵,对称轴是直线,
∴当时,;
即销售单价为元时,每天的销售利润最大,最大利润是元.
26.解:∵二次函数的图象过,两点,
∴,
解得:,
∴这个二次函数的解析式为:;抛物线的对称轴为:,
∴,
∴,
∴;设,
∴,
∴,
∴,
联立:,
解得:或,
∴当或时,.
