冀教版九年级数学上册第27章反比例函数单元检测试卷(有答案)
文档属性
| 名称 | 冀教版九年级数学上册第27章反比例函数单元检测试卷(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 181.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 00:00:00 | ||
图片预览





文档简介
冀教版九年级数学上册
第27章 反比例函数 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
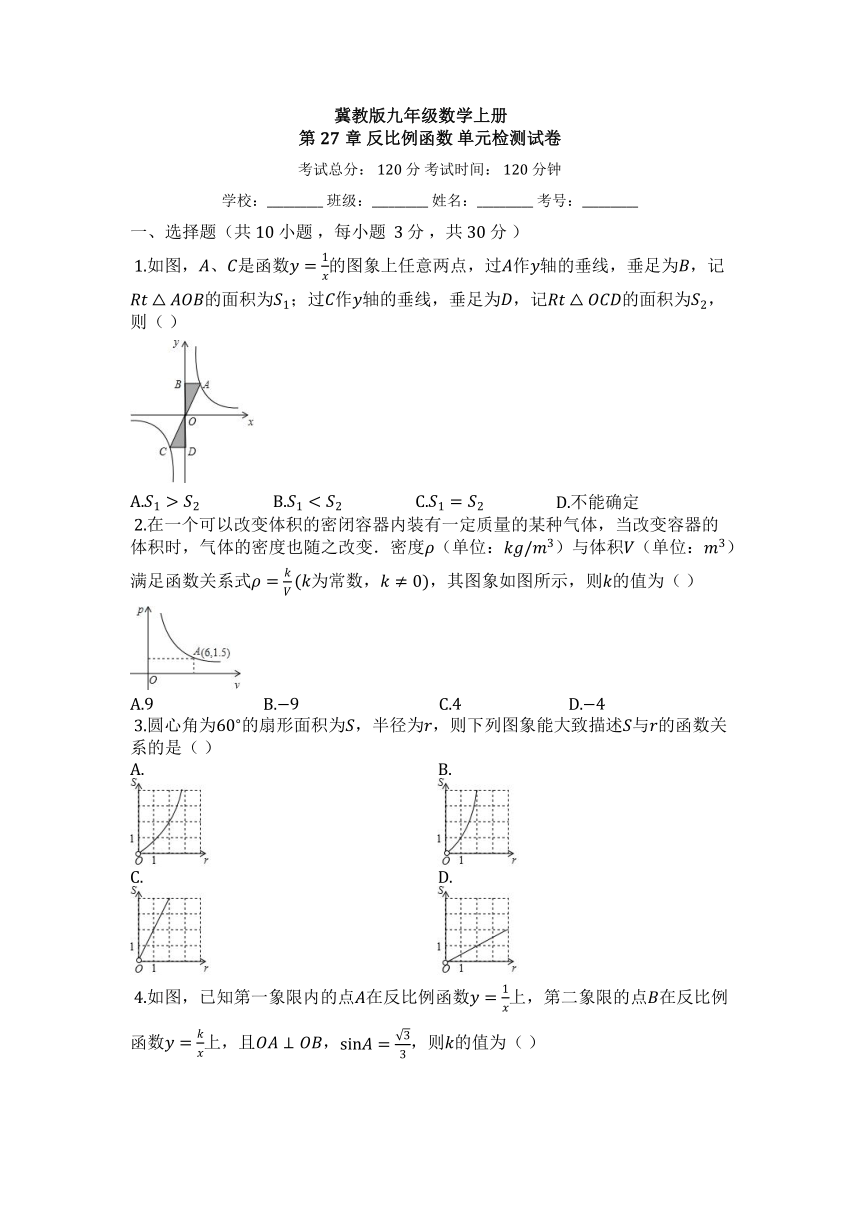
?1.如图,、是函数的图象上任意两点,过作轴的垂线,垂足为,记的面积为;过作轴的垂线,垂足为,记的面积为,则( )
A. B. C. D.不能确定
?2.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也随之改变.密度(单位:)与体积(单位:)满足函数关系式为常数,,其图象如图所示,则的值为( )
A. B. C. D.
?3.圆心角为的扇形面积为,半径为,则下列图象能大致描述与的函数关系的是( )
A. B.
C. D.
?4.如图,已知第一象限内的点在反比例函数上,第二象限的点在反比例函数上,且,,则的值为( )
A. B. C. D.
?5.如图,在直角坐标系中,正方形的中心在原点,且正方形的一组对边与轴平行,点是反比例函数的图象上与正方形的一个交点,若图中阴影部分的面积等于,则的值为( )
A. B. C. D.
?6.,两城间的距离为千米,一人行路的平均速度每小时不少于千米,也不多于千米,则表示此人由到的行路速度(千米/小时)与所用时间(小时)的关系的函数图象是( )
A. B.
C. D.
?7.给出下列四个命题:正确命题的个数是( )
若点在直线上,且点到两坐标轴的距离相等,则点在第一或第四象限;
若、在反比例函数的图象上,则;
一次函数的图象不经过第三象限;
二次函数的最大值是.
A.个 B.个 C.个 D.个
?8.已知一次函数与反比例函数的图象相交于、两点,其横坐标分别是和,当时,实数的取值范围是( )
A.或 B.或
C.或 D.
?9.位于第一象限的点在反比例函数的图象上,点在轴的正半轴上,是坐标原点.若垂直轴,的面积等于,则
A. B. C. D.
?10.如图,在双曲线上取一点向轴引垂线,垂足为,连接,若的面积为,则双曲线的函数关系式为( )
A. B.
C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.学校内要设计一个面积是㎡长方形的运动场,则运动场的长与宽之间的函数关系式为________,当________时运动场是正方形.
?12.如图,正方形的边长为,反比例函数的图象过点,则________.
?13.如图,已知点在反比例函数的图象上,观察图象可知,当时,的取值范围是________.
14.如图,一次函数的图象与反比例函数的图象相交于点和点,当时,应满足什么条件________.
?15.如图,在平面直角坐标系中,正比例函数与反比例函数的图象交于点和.若正比例函数的值大于反比例函数的值,则的取值范围是________.
?16.如图,,,…在函数的图象上,,,,…都是等腰直角三角形,斜边、、,…都在轴上,则的值为________.
?17.某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示.当气球内的气压大于时,气球会将爆炸,为了安全起见,气体的体积应不小于________.
?18.已知如图,点是反比例函数上的任意一点,过点作轴的垂线,垂足为,连接.若的面积是,那么该反比例函数在第二象限的表达式为________.
19.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点左侧固定位置处悬挂重物,在中点右侧用一个弹簧秤向下拉,改变弹簧秤与点的距离,观察弹簧秤的示数的变化情况.实验数据记录如下:
… …
… …
猜测与之间的函数关系,并求出函数关系式为________.
?20.为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量与时间(分钟)的函数关系如图所示.已知,药物燃烧阶段,与成正比例,燃完后与成反比例.现测得药物分钟燃完,此时教室内每立方米空气含药量为.当每立方米空气中含药量低于时,对人体才能无毒害作用.那么从消毒开始,经过________分钟后教室内的空气才能达到安全要求.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,在平面直角坐标系中,函数,常数的图象经过点,且,过点作轴的垂线,垂足为,若面积为,求点的坐标.
?22.如图正比例函数与反比例函数交于点,从向轴、轴分别作垂线,所构成的正方形的面积为.
①分别求出正比例函数与反比例函数的解析式;
②求出正、反比例函数图象的另外一个交点坐标;
③求的面积.
?
23.已知反比函数的图象在第一、三象限.
求的取值范围;
在第一象限的图象上有一点,点的横坐标为,并且点到两坐标轴的距离相等,求反比例函数表达式;
如果,是该函数图象上的点,且,请直接写出的取值范围.
?
24.如图,一条直线与反比例函数的图象交于,两点,与轴交于点,轴,垂足为.
求反比例函数的解析式及点的坐标;
点是线段的中点,点,分别从,两点同时出发,以每秒个单位的速度沿,运动,到点,时停止运动,设运动的时间为.
①求证:.
②若的面积为,求的最小值.
?
25.如图,一次函数的图象交轴于点,且过点.点在反比例函数的图象上.
求该反比例函数的解析式;
连结,求的面积;并结合图形直接写出当函数值时,该反比例函数的自变量的取值范围.
?
26.已知:如图,一次函数的图象与反比例函数的图象交于点.轴于点,轴于点.一次函数的图象分别交轴、轴于点、点,且,.
求点的坐标;
求一次函数与反比例函数的解析式;
根据图象写出当取何值时,一次函数的值小于反比例函数的值?
答案
1.C
2.A
3.A
4.D
5.C
6.D
7.B
8.A
9.B
10.D
11.
12.
13.
14.或
15.或
16.
17.
18.
19.
20.
21.解:∵函数,常数的图象经过点,
∴把代入解析式得,
∴,
∵,
∴,当时,,
∴边上的高是,
而,
∴,
∴把代入,
∴,
∴点的坐标是.
22.解:设正比例函数,反比例函数,
由正方形的面积可得点的坐标,代入两函数表达式可得:,.
则正比例函数的解析式为;反比例函数的解析式为.
∵正、反比例函数图象的另外一个交点是,且点和点关于坐标原点对称,
∵点坐标为,∴点坐标为.
即另一个交点的坐标为.
∵是以点横坐标的绝对值为底边,以点纵坐标的绝对值为高,
∴.
23.解:∵反比函数的图象在第一、三象限,
∴,解得,
∴的取值范围是;∵点在第一象限内,横坐标为,并且点到两坐标轴的距离相等,
∴点坐标为,
代入反比例函数解析式可得,
∴反比例函数表达式为;∵函数图象在第一、三象限,
∴在每个象限内随的增大而减小,
∵,
∴点在第三象限,且,
当点在第一象限时,,满足,
此时,
当点在第三象限时,
∵,
∴,
综上可知当时,的取值范围为或.
24.解:把点代入得:,
∴反比例函数的解析式为:;
把点代入得:,
∴
设直线的解析式为,
把,代入得:,
解得:,,
∴直线的解析式为:,
当时,,
∴点坐标为:;①证明:∵,?,,轴于,
∴,
∴为等腰直角三角形,
∴,
∵为中点,
∴,,,
∴,
∵点,分别从,两点同时出发,以每秒个单位的速度沿,运动,
∴,
在和中,,
∴,
∴;
②解:∵,
∴,
∴,
∴为等腰直角三角形,
∴的面积,
∴的面积最小时,最小,
∵当时,最小,
此时最小值,
∴的面积的最小值.
25.解:∵一次函数的图象过点,
∴.
∴点的坐标为.
∵点在反比例函数的图象上,
∴,即.
∴该反比例函数的解析式为.在中,令,则,得,
∴点的坐标为,
∴.
又∵点的坐标为,
∴中边上的高为.
∴,
当函数值时,即,由函数图象可知自变量的取值范围是:或.
26.解:∵一次函数与轴相交,
∴令,解得,得的坐标为;∵,,
,
,
∴,则,,
∴,
∴,
在中,∴,
即,
∴,故,
把坐标代入,得到,
则一次函数的解析式为:;
把坐标代入反比例函数解析式得,
则反比例解析式为:;根据图象可得:,
解得:或
故直线与双曲线的两个交点为,,
∵,
∴当时,一次函数的值小于反比例函数的值.
第27章 反比例函数 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,、是函数的图象上任意两点,过作轴的垂线,垂足为,记的面积为;过作轴的垂线,垂足为,记的面积为,则( )
A. B. C. D.不能确定
?2.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也随之改变.密度(单位:)与体积(单位:)满足函数关系式为常数,,其图象如图所示,则的值为( )
A. B. C. D.
?3.圆心角为的扇形面积为,半径为,则下列图象能大致描述与的函数关系的是( )
A. B.
C. D.
?4.如图,已知第一象限内的点在反比例函数上,第二象限的点在反比例函数上,且,,则的值为( )
A. B. C. D.
?5.如图,在直角坐标系中,正方形的中心在原点,且正方形的一组对边与轴平行,点是反比例函数的图象上与正方形的一个交点,若图中阴影部分的面积等于,则的值为( )
A. B. C. D.
?6.,两城间的距离为千米,一人行路的平均速度每小时不少于千米,也不多于千米,则表示此人由到的行路速度(千米/小时)与所用时间(小时)的关系的函数图象是( )
A. B.
C. D.
?7.给出下列四个命题:正确命题的个数是( )
若点在直线上,且点到两坐标轴的距离相等,则点在第一或第四象限;
若、在反比例函数的图象上,则;
一次函数的图象不经过第三象限;
二次函数的最大值是.
A.个 B.个 C.个 D.个
?8.已知一次函数与反比例函数的图象相交于、两点,其横坐标分别是和,当时,实数的取值范围是( )
A.或 B.或
C.或 D.
?9.位于第一象限的点在反比例函数的图象上,点在轴的正半轴上,是坐标原点.若垂直轴,的面积等于,则
A. B. C. D.
?10.如图,在双曲线上取一点向轴引垂线,垂足为,连接,若的面积为,则双曲线的函数关系式为( )
A. B.
C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.学校内要设计一个面积是㎡长方形的运动场,则运动场的长与宽之间的函数关系式为________,当________时运动场是正方形.
?12.如图,正方形的边长为,反比例函数的图象过点,则________.
?13.如图,已知点在反比例函数的图象上,观察图象可知,当时,的取值范围是________.
14.如图,一次函数的图象与反比例函数的图象相交于点和点,当时,应满足什么条件________.
?15.如图,在平面直角坐标系中,正比例函数与反比例函数的图象交于点和.若正比例函数的值大于反比例函数的值,则的取值范围是________.
?16.如图,,,…在函数的图象上,,,,…都是等腰直角三角形,斜边、、,…都在轴上,则的值为________.
?17.某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示.当气球内的气压大于时,气球会将爆炸,为了安全起见,气体的体积应不小于________.
?18.已知如图,点是反比例函数上的任意一点,过点作轴的垂线,垂足为,连接.若的面积是,那么该反比例函数在第二象限的表达式为________.
19.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点左侧固定位置处悬挂重物,在中点右侧用一个弹簧秤向下拉,改变弹簧秤与点的距离,观察弹簧秤的示数的变化情况.实验数据记录如下:
… …
… …
猜测与之间的函数关系,并求出函数关系式为________.
?20.为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量与时间(分钟)的函数关系如图所示.已知,药物燃烧阶段,与成正比例,燃完后与成反比例.现测得药物分钟燃完,此时教室内每立方米空气含药量为.当每立方米空气中含药量低于时,对人体才能无毒害作用.那么从消毒开始,经过________分钟后教室内的空气才能达到安全要求.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,在平面直角坐标系中,函数,常数的图象经过点,且,过点作轴的垂线,垂足为,若面积为,求点的坐标.
?22.如图正比例函数与反比例函数交于点,从向轴、轴分别作垂线,所构成的正方形的面积为.
①分别求出正比例函数与反比例函数的解析式;
②求出正、反比例函数图象的另外一个交点坐标;
③求的面积.
?
23.已知反比函数的图象在第一、三象限.
求的取值范围;
在第一象限的图象上有一点,点的横坐标为,并且点到两坐标轴的距离相等,求反比例函数表达式;
如果,是该函数图象上的点,且,请直接写出的取值范围.
?
24.如图,一条直线与反比例函数的图象交于,两点,与轴交于点,轴,垂足为.
求反比例函数的解析式及点的坐标;
点是线段的中点,点,分别从,两点同时出发,以每秒个单位的速度沿,运动,到点,时停止运动,设运动的时间为.
①求证:.
②若的面积为,求的最小值.
?
25.如图,一次函数的图象交轴于点,且过点.点在反比例函数的图象上.
求该反比例函数的解析式;
连结,求的面积;并结合图形直接写出当函数值时,该反比例函数的自变量的取值范围.
?
26.已知:如图,一次函数的图象与反比例函数的图象交于点.轴于点,轴于点.一次函数的图象分别交轴、轴于点、点,且,.
求点的坐标;
求一次函数与反比例函数的解析式;
根据图象写出当取何值时,一次函数的值小于反比例函数的值?
答案
1.C
2.A
3.A
4.D
5.C
6.D
7.B
8.A
9.B
10.D
11.
12.
13.
14.或
15.或
16.
17.
18.
19.
20.
21.解:∵函数,常数的图象经过点,
∴把代入解析式得,
∴,
∵,
∴,当时,,
∴边上的高是,
而,
∴,
∴把代入,
∴,
∴点的坐标是.
22.解:设正比例函数,反比例函数,
由正方形的面积可得点的坐标,代入两函数表达式可得:,.
则正比例函数的解析式为;反比例函数的解析式为.
∵正、反比例函数图象的另外一个交点是,且点和点关于坐标原点对称,
∵点坐标为,∴点坐标为.
即另一个交点的坐标为.
∵是以点横坐标的绝对值为底边,以点纵坐标的绝对值为高,
∴.
23.解:∵反比函数的图象在第一、三象限,
∴,解得,
∴的取值范围是;∵点在第一象限内,横坐标为,并且点到两坐标轴的距离相等,
∴点坐标为,
代入反比例函数解析式可得,
∴反比例函数表达式为;∵函数图象在第一、三象限,
∴在每个象限内随的增大而减小,
∵,
∴点在第三象限,且,
当点在第一象限时,,满足,
此时,
当点在第三象限时,
∵,
∴,
综上可知当时,的取值范围为或.
24.解:把点代入得:,
∴反比例函数的解析式为:;
把点代入得:,
∴
设直线的解析式为,
把,代入得:,
解得:,,
∴直线的解析式为:,
当时,,
∴点坐标为:;①证明:∵,?,,轴于,
∴,
∴为等腰直角三角形,
∴,
∵为中点,
∴,,,
∴,
∵点,分别从,两点同时出发,以每秒个单位的速度沿,运动,
∴,
在和中,,
∴,
∴;
②解:∵,
∴,
∴,
∴为等腰直角三角形,
∴的面积,
∴的面积最小时,最小,
∵当时,最小,
此时最小值,
∴的面积的最小值.
25.解:∵一次函数的图象过点,
∴.
∴点的坐标为.
∵点在反比例函数的图象上,
∴,即.
∴该反比例函数的解析式为.在中,令,则,得,
∴点的坐标为,
∴.
又∵点的坐标为,
∴中边上的高为.
∴,
当函数值时,即,由函数图象可知自变量的取值范围是:或.
26.解:∵一次函数与轴相交,
∴令,解得,得的坐标为;∵,,
,
,
∴,则,,
∴,
∴,
在中,∴,
即,
∴,故,
把坐标代入,得到,
则一次函数的解析式为:;
把坐标代入反比例函数解析式得,
则反比例解析式为:;根据图象可得:,
解得:或
故直线与双曲线的两个交点为,,
∵,
∴当时,一次函数的值小于反比例函数的值.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
