26.1 二次函数课件(23张PPT)
文档属性
| 名称 | 26.1 二次函数课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 10:15:39 | ||
图片预览








文档简介
课件23张PPT。第26章 二次函数26.1 二次函数1课堂讲解二次函数的定义
利用二次函数的表达式表示实际问题2课时流程逐点
导讲练课堂小结作业提升1.函数是什么?
函数的基本概念:在一个变化过程中,有两个变量x和y,
并且对于x每一个确定的值,在y中都有唯一确定的值与
其对应,那么我们就说y是x的函数,也可以说x是自变量,
y是因变量。
2.我们学过了哪些函数?
一次函数、反比例函数1知识点二次函数的定义问题一:
用总长为20 m的围栏材料,一面靠墙,围成一个
矩 形花圃.怎样围才能使花圃的面积最大?知1-导试一试:
我们先列举一些不同的围法,观察矩形花圃的面积
是怎样变化的.如图,设围成的矩形花圃为ABCD,靠墙的
一边为AD,垂直于墙面的两边分别为AB和DC.给出矩形
一边AB的长的一些值(0 可以求出BC的长,从而
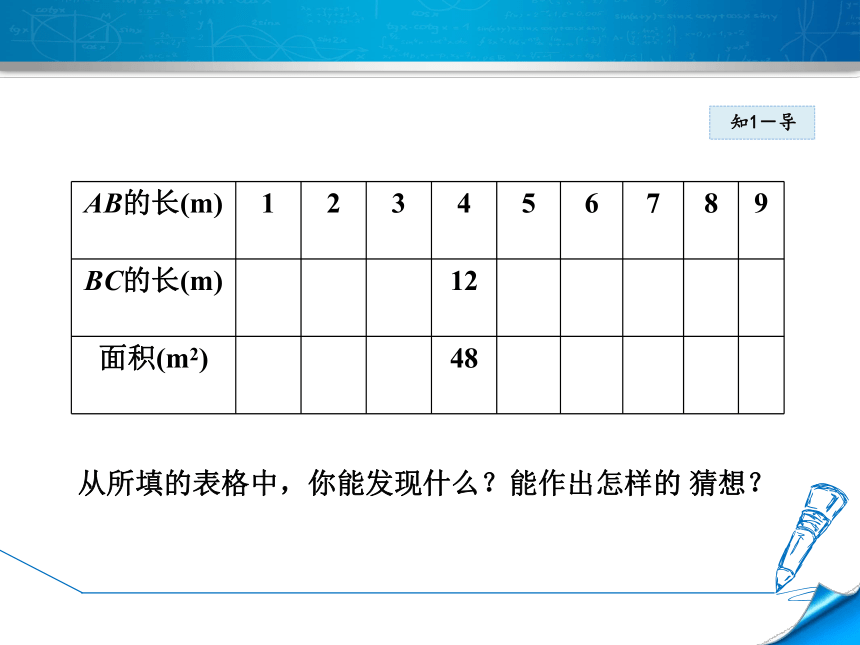
可得矩形的面积.试将计算结
果填人下表的空白处知1-导知1-导从所填的表格中,你能发现什么?能作出怎样的 猜想?知1-导分析:
我们看到,对于一边AB的长的每一个确定 值(0
是说,面积是一边AB的长的函数.问题就归结 为:当
AB的长取何值时,矩形面积的值最大?为此,我 们先
求出这个函数关系式.
设AB的长为 xm,矩形的面积为 ym2,y是x的函
数.试写出这个函数关系式. 例1 下列函数中,哪些是二次函数?并指出二次函数
的二次项系数、一次项系数和常数项.
(1) y=7x-1; (2) y=-5x2;
(3) y=3a3+2a2; (4) y=x-2+x;
(5) y=3(x-2)(x-5); (6) y=x2+ .知1-讲判断一个函数是否为二次函数,要紧扣定义并将其化
简再判断.(1)是一次函数;(2)是二次函数,二次项系
数为-5,一次项系数和常数项为0;(3)中自变量的最
高次数是3,所以不是二次函数;(4)中x-2不是整式,
所以不是二次函数;把(5)整理得到y=3x2-21x+30,
是二次函数,二次项系数为3,一次项系数为-21,
常数项为30;(6)中,因为 是分式,所以不是二次
函数.知1-讲导引:(2)与(5)是二次函数.(2)y=-5x2的二次项系数为-5,
一次项系数和常数项为0;(5)化为一般式,得到y=3x2
-21x+30,所以y=3(x-2)(x-5)的二次项系数为3,
一次项系数为-21,常数项为30.知1-讲解:知1-讲 判断一个函数是否为二次函数,即要看这个函数
的关系式化简后是否同时满足二次函数定义中的三个
条件:
(1)所表示的函数的关系式为整式;
(2)函数的关系式有 唯一自变量;
(3)关系式自变量的最高次数为2且二次项系数不等于0.例2 已知函数y=(a-b)x3+2x2+2+ 是y关
于x的二次函数,求a,b的值.
若是二次函数,则等号的右边应是关于x的二次多
项式,故a-b=0,2a+b-3=0,于是a,b可求.
由题意得知1-讲导引:解:知1-讲 当二次项系数是待定字母时,求出字母的值必须
满足二次项系数不为0这一条件.知1-练下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0
若函数y=(m-2)x2+4x-5(m是常数)是二次函数,
则( )
A.m≠-2 B.m≠2
C.m≠3 D.m≠-3知1-练3 若y=(m-1)xm2+1是二次函数,则m的值是( )
A.1 B.-1 C.1或-1 D.2
关于函数y=(500-10x)(40+x),下列说法不正确
的是( )
A.y是x的二次函数 B.二次项系数是-10
C.一次项是100 D.常数项是20 0002知识点利用二次函数的表达式表示实际问题问题二:
某商店将每件进价为8元的某种商品按每件10元 出售,一天可售出100件该店想通过降低售价、增加销售量的办法来提高利润.经过市场调查,发现这种商品每 件每降价0.1元,每天的销售量可增加10件.将这种商品的售价降低多少时,其每天的销售利润最大?知2-导知2-讲例3 如图,已知等腰直角三角形ABC的直角边长与正方
形MNPQ的边长均为10 cm,AC与MN在同一直线
上,开始时点A与M重合,让△ABC向右移动,最
后点A与点N重合.
问题:
(1)试写出重叠部分面积y(cm2)
与线段MA长度x(cm)
之间的函数关系式;
(2)当MA=1 cm时,重叠部分的面积是多少?知2-讲(1)根据图形及题意所述可得出重叠部分是等腰直角三
角形,从而根据MA的长度可得出y与x之间的函数关
系式;(2)将x=1 cm代入可得出重叠部分的面积.
(1)由题意知,开始时A点与M点重合,让△ABC向右
移动,两图形重叠部分为等腰直角三角形,所以
y= x2(0<x≤10);
(2)当MA=1 cm时,重叠部分的面积是 cm2.导引:解:知2-讲 此题主要考查的是求动态几何图形中面积的函数
关系式,判断出重叠部分是等腰直角三角形比较关键.
在确定实际问题中的函数关系式时,通常根据题目中
的等量关系列出恰当的函数关系式.但要特别注意自
变量的取值范围.知2-练(来自教材)正方形的边长为4,当边长增加x时,面积增加y,
求x与y之间的函数关系式.这 个函数是二次函数吗?知2-练一台机器原价60万元,如果每年的折旧率为x,两年
后这台机器的价格为y万元,则y与x之间的函数表达
式为( )
A.y=60(1-x)2 B.y=60(1-x)
C.y=60-x2 D.y=60(1+x)2知2-练3 下列函数关系中,不是二次函数的是( )
A.边长为x的正方形的面积y与边长x的函数关系
B.一个直角三角形两条直角边长的和是6,则这个
直角三角形的面积y与一条直角边长x的函数关系
C.在边长为5的正方形内挖去一个边长为t的小正方
形,剩余面积S与t的函数关系
D.多边形的内角和m与边数n的函数关系 1.请叙述二次函数的定义.
2. 许多实际问题可以转化为二次函数来解决,请你联
系生活实际,编一道二次函数应用题,并写出函数
关系式。
利用二次函数的表达式表示实际问题2课时流程逐点
导讲练课堂小结作业提升1.函数是什么?
函数的基本概念:在一个变化过程中,有两个变量x和y,
并且对于x每一个确定的值,在y中都有唯一确定的值与
其对应,那么我们就说y是x的函数,也可以说x是自变量,
y是因变量。
2.我们学过了哪些函数?
一次函数、反比例函数1知识点二次函数的定义问题一:
用总长为20 m的围栏材料,一面靠墙,围成一个
矩 形花圃.怎样围才能使花圃的面积最大?知1-导试一试:
我们先列举一些不同的围法,观察矩形花圃的面积
是怎样变化的.如图,设围成的矩形花圃为ABCD,靠墙的
一边为AD,垂直于墙面的两边分别为AB和DC.给出矩形
一边AB的长的一些值(0
可得矩形的面积.试将计算结
果填人下表的空白处知1-导知1-导从所填的表格中,你能发现什么?能作出怎样的 猜想?知1-导分析:
我们看到,对于一边AB的长的每一个确定 值(0
AB的长取何值时,矩形面积的值最大?为此,我 们先
求出这个函数关系式.
设AB的长为 xm,矩形的面积为 ym2,y是x的函
数.试写出这个函数关系式. 例1 下列函数中,哪些是二次函数?并指出二次函数
的二次项系数、一次项系数和常数项.
(1) y=7x-1; (2) y=-5x2;
(3) y=3a3+2a2; (4) y=x-2+x;
(5) y=3(x-2)(x-5); (6) y=x2+ .知1-讲判断一个函数是否为二次函数,要紧扣定义并将其化
简再判断.(1)是一次函数;(2)是二次函数,二次项系
数为-5,一次项系数和常数项为0;(3)中自变量的最
高次数是3,所以不是二次函数;(4)中x-2不是整式,
所以不是二次函数;把(5)整理得到y=3x2-21x+30,
是二次函数,二次项系数为3,一次项系数为-21,
常数项为30;(6)中,因为 是分式,所以不是二次
函数.知1-讲导引:(2)与(5)是二次函数.(2)y=-5x2的二次项系数为-5,
一次项系数和常数项为0;(5)化为一般式,得到y=3x2
-21x+30,所以y=3(x-2)(x-5)的二次项系数为3,
一次项系数为-21,常数项为30.知1-讲解:知1-讲 判断一个函数是否为二次函数,即要看这个函数
的关系式化简后是否同时满足二次函数定义中的三个
条件:
(1)所表示的函数的关系式为整式;
(2)函数的关系式有 唯一自变量;
(3)关系式自变量的最高次数为2且二次项系数不等于0.例2 已知函数y=(a-b)x3+2x2+2+ 是y关
于x的二次函数,求a,b的值.
若是二次函数,则等号的右边应是关于x的二次多
项式,故a-b=0,2a+b-3=0,于是a,b可求.
由题意得知1-讲导引:解:知1-讲 当二次项系数是待定字母时,求出字母的值必须
满足二次项系数不为0这一条件.知1-练下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0
若函数y=(m-2)x2+4x-5(m是常数)是二次函数,
则( )
A.m≠-2 B.m≠2
C.m≠3 D.m≠-3知1-练3 若y=(m-1)xm2+1是二次函数,则m的值是( )
A.1 B.-1 C.1或-1 D.2
关于函数y=(500-10x)(40+x),下列说法不正确
的是( )
A.y是x的二次函数 B.二次项系数是-10
C.一次项是100 D.常数项是20 0002知识点利用二次函数的表达式表示实际问题问题二:
某商店将每件进价为8元的某种商品按每件10元 出售,一天可售出100件该店想通过降低售价、增加销售量的办法来提高利润.经过市场调查,发现这种商品每 件每降价0.1元,每天的销售量可增加10件.将这种商品的售价降低多少时,其每天的销售利润最大?知2-导知2-讲例3 如图,已知等腰直角三角形ABC的直角边长与正方
形MNPQ的边长均为10 cm,AC与MN在同一直线
上,开始时点A与M重合,让△ABC向右移动,最
后点A与点N重合.
问题:
(1)试写出重叠部分面积y(cm2)
与线段MA长度x(cm)
之间的函数关系式;
(2)当MA=1 cm时,重叠部分的面积是多少?知2-讲(1)根据图形及题意所述可得出重叠部分是等腰直角三
角形,从而根据MA的长度可得出y与x之间的函数关
系式;(2)将x=1 cm代入可得出重叠部分的面积.
(1)由题意知,开始时A点与M点重合,让△ABC向右
移动,两图形重叠部分为等腰直角三角形,所以
y= x2(0<x≤10);
(2)当MA=1 cm时,重叠部分的面积是 cm2.导引:解:知2-讲 此题主要考查的是求动态几何图形中面积的函数
关系式,判断出重叠部分是等腰直角三角形比较关键.
在确定实际问题中的函数关系式时,通常根据题目中
的等量关系列出恰当的函数关系式.但要特别注意自
变量的取值范围.知2-练(来自教材)正方形的边长为4,当边长增加x时,面积增加y,
求x与y之间的函数关系式.这 个函数是二次函数吗?知2-练一台机器原价60万元,如果每年的折旧率为x,两年
后这台机器的价格为y万元,则y与x之间的函数表达
式为( )
A.y=60(1-x)2 B.y=60(1-x)
C.y=60-x2 D.y=60(1+x)2知2-练3 下列函数关系中,不是二次函数的是( )
A.边长为x的正方形的面积y与边长x的函数关系
B.一个直角三角形两条直角边长的和是6,则这个
直角三角形的面积y与一条直角边长x的函数关系
C.在边长为5的正方形内挖去一个边长为t的小正方
形,剩余面积S与t的函数关系
D.多边形的内角和m与边数n的函数关系 1.请叙述二次函数的定义.
2. 许多实际问题可以转化为二次函数来解决,请你联
系生活实际,编一道二次函数应用题,并写出函数
关系式。
