26.2 .1 二次函数y=ax2的图象与性质 导学案(含答案)
文档属性
| 名称 | 26.2 .1 二次函数y=ax2的图象与性质 导学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 85.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 11:22:54 | ||
图片预览


文档简介
26.2.1二次函数y=ax2的图像和性质导学案
学习目标
1.会画二次函数y=ax2的图像,知道其图像是一条抛物线.
2.掌握二次函数y=ax2的性质,会解决简单的问题.
学习策略
1.自己动手画图,运用图像分析理解函数的性质.
2.牢记二次函数的y=ax2的图像和性质.
学习过程
一.复习回顾:
1.什么是二次函数?
2. 1. 圆的面积公式S=πR2中,S与R之间的关系是( )
A.S是R的正比例函数
B.S是R的一次函数
C.S是R的二次函数
D.以上答案都不对
3. 画函数图像的步骤方法是什么?一次函数的图像和性质是如何探究的?
4.你能画出二次函数的图像吗?
二.新课学习:
1.自学教材P5,回答以下问题:
1、一次函数的图像是什么形状?二次函数的图像也会是一条直线吗?
2、回忆函数图像的画法:1列表,2描点,3连线..
3、自己独立画出二次函数y=x2的图像?对照例1分析在列表取点时要注意哪些问题?
4、观察图像的形状,理解“抛物线”, 抛物线是轴对称图形吗?若是,它的对称轴是什么?什么是抛物线的顶点?
2、自学课本P6,思考以下问题:
1、独立画出二次函数y=-x2的图像,y=2x2的图像y=-2x2的图像:
2、比较分析,它们的开口方向,对称轴,顶点有何区别与联系,与a的值有何关系?
3、观察图像,当a>0时,抛物线有什么变化趋势?当a<0时图像是怎样变化的?总结y=ax2的增减性.
4、根据抛物线的顶点总结二次函数的最大值和最小值问题.
三.尝试应用:
1. 在同一坐标系中,作y=x2,y=﹣x2,y=x2的图象,它们的共同特点是( )
A.抛物线的开口方向向上B.都是关于x轴对称的抛物线,且y随x的增大而增大C.都是关于y轴对称的抛物线,且y随x的增大而减小D.都是关于y轴对称的抛物线,有公共的顶点
2. 二次函数y=(m-1)x2的图像开口向下,则m=
3. 已知二次函数y=a2(a≠0)的图像经过点(-2,-3)?
(1)求a的值,并写出这个二次函数的解析式?
(2)说出这个二次函数图像的顶点坐标、对称性、开口方向和图像的位置
四.自主总结:
开口方向
顶点
对称轴
增减性
最值
a>0
y轴
x>0,y随x的增大而 ;x<0时,y随x的增大而减小;
x=0时,y有最小值为
a<0
y轴
x>0,y随x的增大而 ;x<0时,y随x的增大而增大;
x=0时,y有最大值为
五.达标测试
一.选择题(共3小题)
1.在同一坐标系中,作y=x2,y=﹣x2,y=x2的图象,它们的共同特点是( )
A.抛物线的开口方向向上
B.都是关于x轴对称的抛物线,且y随x的增大而增大
C.都是关于y轴对称的抛物线,且y随x的增大而减小
D.都是关于y轴对称的抛物线,有公共的顶点
2.抛物线y=4x2与y=﹣2x2的图象,开口较大的是( )
A.y=﹣2x2 B.y=4x2 C.同样大 D.无法确定
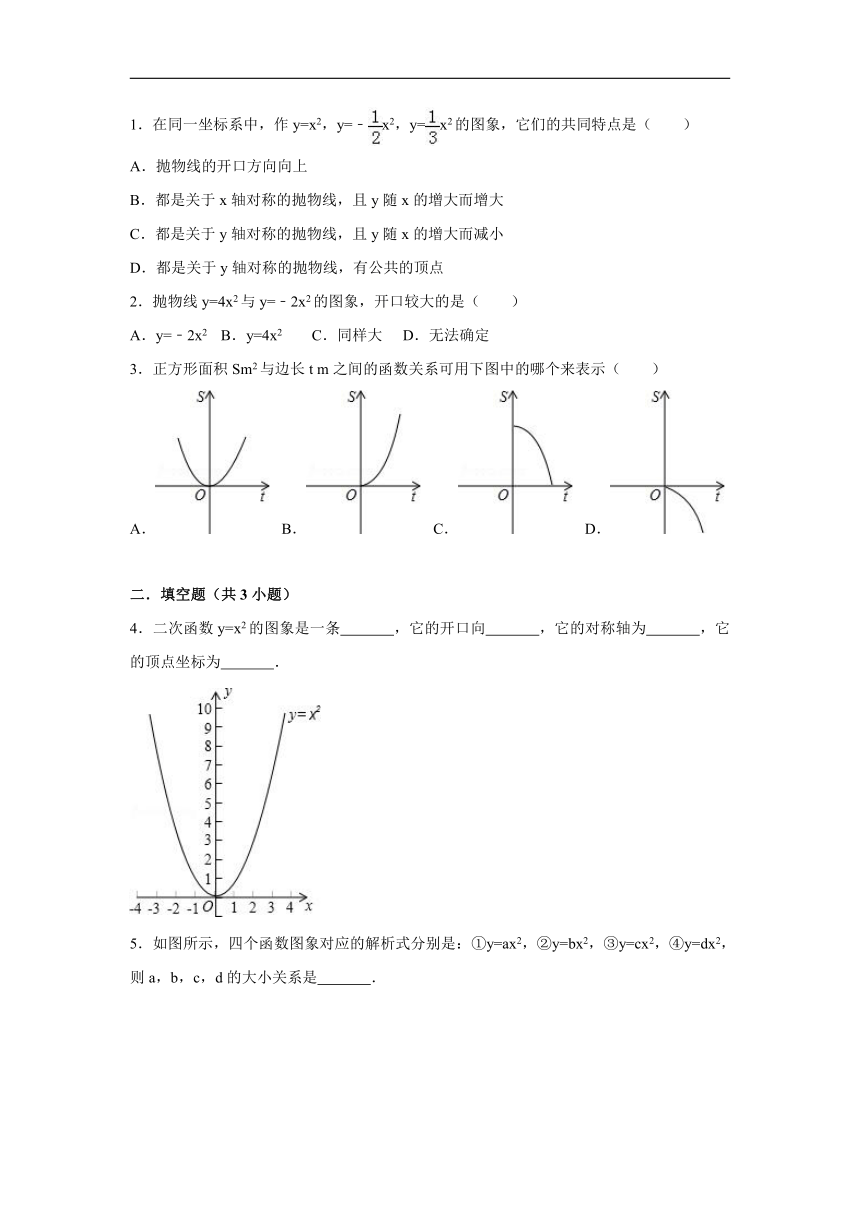
3.正方形面积Sm2与边长t m之间的函数关系可用下图中的哪个来表示( )
A. B. C. D.
二.填空题(共3小题)
4.二次函数y=x2的图象是一条 ,它的开口向 ,它的对称轴为 ,它的顶点坐标为 .
5.如图所示,四个函数图象对应的解析式分别是:①y=ax2,②y=bx2,③y=cx2,④y=dx2,则a,b,c,d的大小关系是 .
6.如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=x2与y=﹣x2的图象,则阴影部分的面积是 .
三.解答题(共2小题)
7.在同一平面直角坐标系中,画出下列函数的图象.
(1)y=2x2; (2)y=x2.
8.在同一直角坐标系中作出y=3x2和y=﹣3x2的图象,并比较两者的异同.
1. 【分析】本题的三个抛物线解析式都符合y=ax2形式,可以从顶点坐标和对称轴找相同点.
【解答】解:因为y=ax2形式的二次函数对称轴都是y轴,且顶点都在原点,
所以它们的共同特点是:关于y轴对称的抛物线,有公共的顶点.
故选D.
2. 【分析】根据|a|越大开口就越小,|a|越小开口就越大求解即可.
【解答】解:抛物线y=4x2与y=﹣2x2的图象中|4|=4,|﹣2|=2,
∵4>2,
∴抛物线y=4x2的开口小于y=﹣2x2的开口,
故选A.
3. 【分析】根据正方形的面积公式列出式子,判断S与t的函数关系找二次函数,结合自变量的取值范围,选择图象.
【解答】解:根据题意可知:S=t2,(t≥0).
∴图象是抛物线且在第一象限.
故选:B.
4. 【分析】此题较简单,观察图象即可得出答案.
【解答】解:观察图象可知,
二次函数y=x2的图象是一条抛物线,
它的开口向上,它的对称轴为y轴,它的顶点坐标为(0,0).
5. 【分析】设x=1,函数值分别等于二次项系数,根据图象,比较各对应点纵坐标的大小
【解答】解:因为直线x=1与四条抛物线的交点从上到下依次为(1,a),(1,b),(1,c),(1,d),
所以,a>b>c>d.
故答案为:a>b>c>d.
6. 【分析】根据题意,观察图形可得图中的阴影部分的面积是图中正方形面积的一半,而正方形面积为16,由此可以求出阴影部分的面积.
【解答】解:∵函数y=x2与y=﹣x2的图象关于x轴对称,
∴图中的阴影部分的面积是图中正方形面积的一半,
而边长为4的正方形面积为16,
所以图中的阴影部分的面积是8.
故答案为8.
7. 【分析】利用列表、描点、连线的方法作出两个函数的图象即可.
【解答】解:列表得:
﹣2
﹣1
0
1
2
y=2x2
8
2
0
2
8
y=x2
2
0
2
描点、连线可得图象为:
8. 【分析】根据二次函数解析式符合y=ax2得出图象,进而得出图象的异同即可.
【解答】解:如图所示:
两图象开口大小形状相同,但是开口方向不同.
学习目标
1.会画二次函数y=ax2的图像,知道其图像是一条抛物线.
2.掌握二次函数y=ax2的性质,会解决简单的问题.
学习策略
1.自己动手画图,运用图像分析理解函数的性质.
2.牢记二次函数的y=ax2的图像和性质.
学习过程
一.复习回顾:
1.什么是二次函数?
2. 1. 圆的面积公式S=πR2中,S与R之间的关系是( )
A.S是R的正比例函数
B.S是R的一次函数
C.S是R的二次函数
D.以上答案都不对
3. 画函数图像的步骤方法是什么?一次函数的图像和性质是如何探究的?
4.你能画出二次函数的图像吗?
二.新课学习:
1.自学教材P5,回答以下问题:
1、一次函数的图像是什么形状?二次函数的图像也会是一条直线吗?
2、回忆函数图像的画法:1列表,2描点,3连线..
3、自己独立画出二次函数y=x2的图像?对照例1分析在列表取点时要注意哪些问题?
4、观察图像的形状,理解“抛物线”, 抛物线是轴对称图形吗?若是,它的对称轴是什么?什么是抛物线的顶点?
2、自学课本P6,思考以下问题:
1、独立画出二次函数y=-x2的图像,y=2x2的图像y=-2x2的图像:
2、比较分析,它们的开口方向,对称轴,顶点有何区别与联系,与a的值有何关系?
3、观察图像,当a>0时,抛物线有什么变化趋势?当a<0时图像是怎样变化的?总结y=ax2的增减性.
4、根据抛物线的顶点总结二次函数的最大值和最小值问题.
三.尝试应用:
1. 在同一坐标系中,作y=x2,y=﹣x2,y=x2的图象,它们的共同特点是( )
A.抛物线的开口方向向上B.都是关于x轴对称的抛物线,且y随x的增大而增大C.都是关于y轴对称的抛物线,且y随x的增大而减小D.都是关于y轴对称的抛物线,有公共的顶点
2. 二次函数y=(m-1)x2的图像开口向下,则m=
3. 已知二次函数y=a2(a≠0)的图像经过点(-2,-3)?
(1)求a的值,并写出这个二次函数的解析式?
(2)说出这个二次函数图像的顶点坐标、对称性、开口方向和图像的位置
四.自主总结:
开口方向
顶点
对称轴
增减性
最值
a>0
y轴
x>0,y随x的增大而 ;x<0时,y随x的增大而减小;
x=0时,y有最小值为
a<0
y轴
x>0,y随x的增大而 ;x<0时,y随x的增大而增大;
x=0时,y有最大值为
五.达标测试
一.选择题(共3小题)
1.在同一坐标系中,作y=x2,y=﹣x2,y=x2的图象,它们的共同特点是( )
A.抛物线的开口方向向上
B.都是关于x轴对称的抛物线,且y随x的增大而增大
C.都是关于y轴对称的抛物线,且y随x的增大而减小
D.都是关于y轴对称的抛物线,有公共的顶点
2.抛物线y=4x2与y=﹣2x2的图象,开口较大的是( )
A.y=﹣2x2 B.y=4x2 C.同样大 D.无法确定
3.正方形面积Sm2与边长t m之间的函数关系可用下图中的哪个来表示( )
A. B. C. D.
二.填空题(共3小题)
4.二次函数y=x2的图象是一条 ,它的开口向 ,它的对称轴为 ,它的顶点坐标为 .
5.如图所示,四个函数图象对应的解析式分别是:①y=ax2,②y=bx2,③y=cx2,④y=dx2,则a,b,c,d的大小关系是 .
6.如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=x2与y=﹣x2的图象,则阴影部分的面积是 .
三.解答题(共2小题)
7.在同一平面直角坐标系中,画出下列函数的图象.
(1)y=2x2; (2)y=x2.
8.在同一直角坐标系中作出y=3x2和y=﹣3x2的图象,并比较两者的异同.
1. 【分析】本题的三个抛物线解析式都符合y=ax2形式,可以从顶点坐标和对称轴找相同点.
【解答】解:因为y=ax2形式的二次函数对称轴都是y轴,且顶点都在原点,
所以它们的共同特点是:关于y轴对称的抛物线,有公共的顶点.
故选D.
2. 【分析】根据|a|越大开口就越小,|a|越小开口就越大求解即可.
【解答】解:抛物线y=4x2与y=﹣2x2的图象中|4|=4,|﹣2|=2,
∵4>2,
∴抛物线y=4x2的开口小于y=﹣2x2的开口,
故选A.
3. 【分析】根据正方形的面积公式列出式子,判断S与t的函数关系找二次函数,结合自变量的取值范围,选择图象.
【解答】解:根据题意可知:S=t2,(t≥0).
∴图象是抛物线且在第一象限.
故选:B.
4. 【分析】此题较简单,观察图象即可得出答案.
【解答】解:观察图象可知,
二次函数y=x2的图象是一条抛物线,
它的开口向上,它的对称轴为y轴,它的顶点坐标为(0,0).
5. 【分析】设x=1,函数值分别等于二次项系数,根据图象,比较各对应点纵坐标的大小
【解答】解:因为直线x=1与四条抛物线的交点从上到下依次为(1,a),(1,b),(1,c),(1,d),
所以,a>b>c>d.
故答案为:a>b>c>d.
6. 【分析】根据题意,观察图形可得图中的阴影部分的面积是图中正方形面积的一半,而正方形面积为16,由此可以求出阴影部分的面积.
【解答】解:∵函数y=x2与y=﹣x2的图象关于x轴对称,
∴图中的阴影部分的面积是图中正方形面积的一半,
而边长为4的正方形面积为16,
所以图中的阴影部分的面积是8.
故答案为8.
7. 【分析】利用列表、描点、连线的方法作出两个函数的图象即可.
【解答】解:列表得:
﹣2
﹣1
0
1
2
y=2x2
8
2
0
2
8
y=x2
2
0
2
描点、连线可得图象为:
8. 【分析】根据二次函数解析式符合y=ax2得出图象,进而得出图象的异同即可.
【解答】解:如图所示:
两图象开口大小形状相同,但是开口方向不同.
