2018-2019学年上海市浦东新区华师大二附中高一(下)期中数学试卷解析版
文档属性
| 名称 | 2018-2019学年上海市浦东新区华师大二附中高一(下)期中数学试卷解析版 |

|
|
| 格式 | zip | ||
| 文件大小 | 94.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 16:40:28 | ||
图片预览


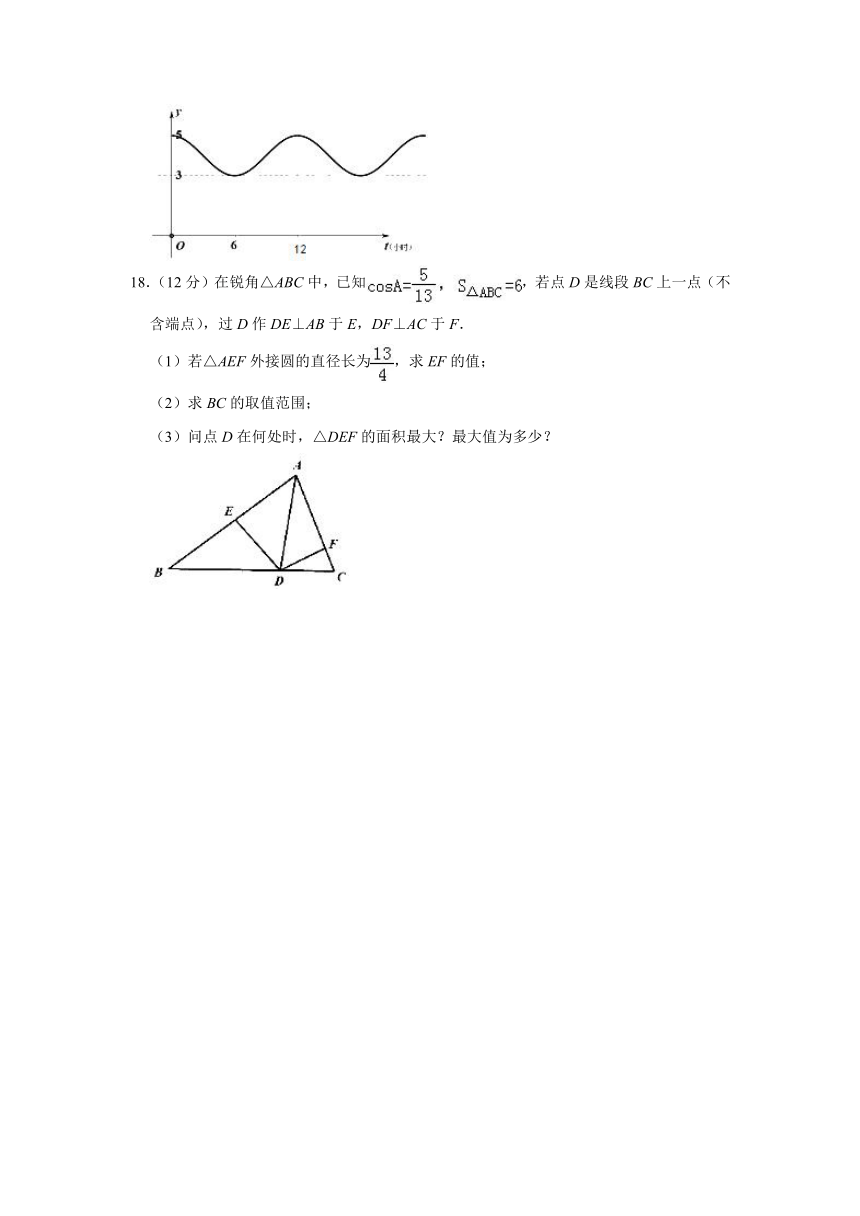


文档简介
2018-2019学年上海市浦东新区华师大二附中高一(下)期中数学试卷
一、填空题(每小题4分,共40分)
1.2019°是第 象限.
2.已知角α的终边经过点P(2,﹣3),则sinα=
3.已知tanα=2,则= .
4.函数y=的定义域为 .
5.已知,则= .
6.已知在第二象限,则= .
7.方程5sinx=4+2cos2x的解集为 .
8.已知,则= .
9.将函数y=sin2x的图象先沿x轴向左平移个单位,再将所有点的横坐标伸长到原来的2倍(纵坐标不变)后得到函数y=f(x)图象,对于函数y=f(x)有以下四个判断:
①该函数的解析式为;
②该函数图象关于点对称;
③该函数在上是增函数;
④若函数y=f(x)+a在上的最小值为1,则.
其中正确判断的序号是 (写出所有正确判断的序号).
10.已知△ABC中,7sin2B+3sin2C=2sin2A+2sinAsinBsinC,则= .
二、选择题(每小题4分,共16分)
11.如果α是第三象限的角,那么必然不是下列哪个象限的角( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.函数的反函数是( )
A. B.
C. D.
13.在△ABC中,三个内角A,B,C所对的边分别为a,b,c.已知2acosB=c,且满足 sinAsinB(2﹣cosC)=sin2+,则△ABC为( )
A.锐角非等边三角形 B.等边三角形
C.等腰直角三角形 D.钝角三角形
14.已知函数f(x)=cos(3x+φ)满足f(x)≤f(1)恒成立,则( )
A.函数f(x﹣1)一定是奇函数
B.函数f(x+1)一定是奇函数
C.函数f(x﹣1)一定是偶函数
D.函数f(x+1)一定是偶函数
三、解答题(共44分)
15.(8分)已知.
(1)求sinαcosα的值;
(2)若α为第二象限的角,求的值.
16.(12分)已知函数f(x)=Asin(ωx+φ)(其中)的相邻对称轴之间的距离为,且该函数图象的一个最高点为.
(1)求函数f(x)的解析式和单调递增区间;
(2)若,求函数f(x)的最大值和最小值.
17.(12分)如图,甲、乙两个企业的用电负荷量y关于投产持续时间t(单位:小时)的关系y=f(t)均近似地满足函数f(t)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π).
(1)根据图象,求函数f(t)的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过9,现采用错峰用电的方式,让企业乙比企业甲推迟m(m>0)小时投产,求m的最小值.
18.(12分)在锐角△ABC中,已知,若点D是线段BC上一点(不含端点),过D作DE⊥AB于E,DF⊥AC于F.
(1)若△AEF外接圆的直径长为,求EF的值;
(2)求BC的取值范围;
(3)问点D在何处时,△DEF的面积最大?最大值为多少?
2018-2019学年上海市浦东新区华师大二附中高一(下)期中数学试卷
参考答案与试题解析
一、填空题(每小题4分,共40分)
1.【解答】解:2019°=360°×5+219°,是第三象限角.
故答案为:三.
2.【解答】解:∵角α的终边经过点P(2,﹣3),则 x=2,y=﹣3,r=|OP|==,
∴sinα==,
故答案为:﹣.
3.【解答】解:tanα=2,则===.
故答案为:
4.【解答】解:根据函数y=,可得cosx≥0,可得 2kπ﹣≤x≤2kπ+(k∈Z),
故函数的定义域为[2kπ﹣,2kπ+],k∈Z,
故答案为:[2kπ﹣,2kπ+],k∈Z.
5.【解答】解:由,
得﹣cos,即cos,
∴sinα=,则tanα==.
∴=﹣cot()=﹣tanα=.
故答案为:.
6.【解答】解:若在第二象限,
∴cosα=﹣,
则=====2,
故答案为:2
7.【解答】解:方程5sinx=4+2cos2x可化为5sinx=4+2(1﹣2sin2x),
即4sin2x+5sinx﹣6=0,
解得sinx=,或sinx=﹣2(不合题意,舍去);
所以该方程的解集为{x|x=arcsin+2kπ,或x=π﹣arcsin+2kπ,k∈Z}.
故答案为:{x|x=arcsin+2kπ,或x=π﹣arcsin+2kπ,k∈Z}.
8.【解答】解:由,得2sinα=,
∴,则tanα=.
由tan==1,解得tan=(舍)或.
∴===.
故答案为:.
9.【解答】解:根据题意知,f(x)=sin(x),令x=则,y=≠0
∴①②错误;由三角函数的性质知③④正确;
故答案为③④.
10.【解答】解:7sin2B+3sin2C=2sin2A+2sinAsinBsinC,
由正弦定理可得:7b2+3c2=2a2+2bcsinA,
∴a2=,又a2=b2+c2﹣2bccosA,
∴=b2+c2﹣2bccosA,
化为:2(sinA﹣2cosA)==≥2=2,
当且仅当b=c时取等号.
即2sin(A﹣θ)≥2,其中tanθ=2,sinθ=,cosθ=.
即sin(A﹣θ)≥1,又sin(A﹣θ)≤1,
∴sin(A﹣θ)=1.
∴A﹣θ=+2kπ,即A=θ++2kπ,k∈N*.
∴sin(A+)=sin(θ+++2kπ)=cos(θ+)
=(cosθ﹣sinθ)=×(﹣)=﹣.
∴=cos()=sin(A+)=.
故答案为:﹣.
二、选择题(每小题4分,共16分)
11.【解答】解:α是第三象限的角,则α∈(2kπ+π,2kπ+),k∈Z,
所以∈(kπ+,kπ+),k∈Z;
所以可以是第一、第三、或第四象限角.
故选:B.
12.【解答】解:函数的反函数是y=﹣cosx,x∈[0,π],
故选:D.
13.【解答】解:将已知等式2acosB=c,利用正弦定理化简得:2sinAcosB=sinC,
∵sinC=sin(A+B)=sinAcosB+cosAsinB,
∴2sinAcosB=sinAcosB+cosAsinB,即sinAcosB﹣cosAsinB=sin(A﹣B)=0,
∵A与B都为△ABC的内角,
∴A﹣B=0,即A=B,
已知第二个等式变形得:sinAsinB(2﹣cosC)=(1﹣cosC)+=1﹣cosC,
﹣[cos(A+B)﹣cos(A﹣B)](2﹣cosC)=1﹣cosC,
∴﹣(﹣cosC﹣1)(2﹣cosC)=1﹣cosC,
即(cosC+1)(2﹣cosC)=2﹣cosC,
整理得:cos2C﹣2cosC=0,即cosC(cosC﹣2)=0,
∴cosC=0或cosC=2(舍去),
∴C=90°,
则△ABC为等腰直角三角形.
故选:C.
14.【解答】解:由函数f(x)=cos(3x+φ)满足f(x)≤f(1)恒成立,
得函数f(x)的图象关于直线x=1对称,
即函数f(x+1)一定为偶函数,
故选:D.
三、解答题(共44分)
15.【解答】解:(1)∵,∴平方得sin2α+2sinαcosα+cos2α=,
得2sinαcosα=﹣1=﹣,
得sinαcosα=﹣.
(2)若α为第二象限的角,sinα>0,cosα<0,
则=+===﹣.
16.【解答】解:(1)由题意有:A=2,T=π,即ω==2,
由当x=时,函数f(x)取最大值,即2×+φ=2k,解得φ=2kπ,又0<φ,所以φ=,
即f(x)=2sin(2x+),
令2kπ≤2x+,得:k,(k∈Z)
故函数f(x)的解析式为:f(x)=2sin(2x+).
函数f(x)的单调递增区间为:[kπ,k](k∈Z).
(2)当,
则2x+∈[,],
所以2sin(2x+)∈[1,2],
故函数f(x)的最大值为2,最小值为1.
17.【解答】(本题满分为14分)
解:(1)由图知T=12=,∴ω=,…(1分)
A+b=5,b﹣A=3,可得:A=1,b=4,…(3分)
∴f(t)=sin(x+φ)+4,
代入(0,5),得φ=+2kπ,
又0<φ<π,
∴φ=…(5分)
即f(t)=sin(t+)+4,…(6分)
(2)设乙投产持续时间为t小时,则甲的投产持续时间为(t+m)小时,
由诱导公式,企业乙用电负荷量随持续时间t变化的关系式为:f(t)=cost+4;
同理,企业甲用电负荷量变化关系式为:f(t+m)=cos(t+m)+4;
两企业用电负荷量之和f(t+m)+f(t)=cos(t+m)+cost+8(t≥0);﹣﹣﹣﹣﹣﹣(8分)
依题意,有f(t+m)+f(t)=cos(t+m)+cost+8≤9恒成立,
即cos (t+m)+cos t≤1恒成立,
展开有:(cos m+1)cost﹣sinmsint≤1恒成立,﹣﹣﹣﹣﹣﹣(10分)
∵(cos m+1)cos t﹣sin msin t=Acos(t+?),
(其中,A=,cos?=;sin?=);
∴A=≤1,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)
整理得到:cos m≤﹣,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)
依据余弦函数图象得:+2kπ≤m≤+2kπ,(k∈Z),
即12k+4≤m≤12+8,取k=0得:4≤m≤8
∴m的最小值为4.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)
18.【解答】解:(1)∵在锐角△ABC中,,∴sinA=,
∵bc?,
∴bc=13,
∵△AEF外接圆的直径长为,
由正弦定理可得,==,
∴EF=3;
(2)在△ABC中,由余弦定理得,
BC2=b2+c2﹣2bccosA
=b2+c2﹣10≥2bc﹣10=16,
当且仅当b=c=时取等号,
∴BC≥4;
BC的取值范围:[4,+);
(3)设S△ABD=x,则S△ADC=6﹣x,
∵,
∴AB?AC=,
∵DE⊥AB于E,DF⊥AC于F,
∴,,
∴,,
∵
=
=
=﹣,
∴当x=3时,S△EDF的最大值为,.
∴当x=3时,三角形ABD与三角形ADC面积相等
∴D为BC的中点,
∴当D为BC的中点时,△DEF的面积最大,最大值为.△
一、填空题(每小题4分,共40分)
1.2019°是第 象限.
2.已知角α的终边经过点P(2,﹣3),则sinα=
3.已知tanα=2,则= .
4.函数y=的定义域为 .
5.已知,则= .
6.已知在第二象限,则= .
7.方程5sinx=4+2cos2x的解集为 .
8.已知,则= .
9.将函数y=sin2x的图象先沿x轴向左平移个单位,再将所有点的横坐标伸长到原来的2倍(纵坐标不变)后得到函数y=f(x)图象,对于函数y=f(x)有以下四个判断:
①该函数的解析式为;
②该函数图象关于点对称;
③该函数在上是增函数;
④若函数y=f(x)+a在上的最小值为1,则.
其中正确判断的序号是 (写出所有正确判断的序号).
10.已知△ABC中,7sin2B+3sin2C=2sin2A+2sinAsinBsinC,则= .
二、选择题(每小题4分,共16分)
11.如果α是第三象限的角,那么必然不是下列哪个象限的角( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.函数的反函数是( )
A. B.
C. D.
13.在△ABC中,三个内角A,B,C所对的边分别为a,b,c.已知2acosB=c,且满足 sinAsinB(2﹣cosC)=sin2+,则△ABC为( )
A.锐角非等边三角形 B.等边三角形
C.等腰直角三角形 D.钝角三角形
14.已知函数f(x)=cos(3x+φ)满足f(x)≤f(1)恒成立,则( )
A.函数f(x﹣1)一定是奇函数
B.函数f(x+1)一定是奇函数
C.函数f(x﹣1)一定是偶函数
D.函数f(x+1)一定是偶函数
三、解答题(共44分)
15.(8分)已知.
(1)求sinαcosα的值;
(2)若α为第二象限的角,求的值.
16.(12分)已知函数f(x)=Asin(ωx+φ)(其中)的相邻对称轴之间的距离为,且该函数图象的一个最高点为.
(1)求函数f(x)的解析式和单调递增区间;
(2)若,求函数f(x)的最大值和最小值.
17.(12分)如图,甲、乙两个企业的用电负荷量y关于投产持续时间t(单位:小时)的关系y=f(t)均近似地满足函数f(t)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π).
(1)根据图象,求函数f(t)的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过9,现采用错峰用电的方式,让企业乙比企业甲推迟m(m>0)小时投产,求m的最小值.
18.(12分)在锐角△ABC中,已知,若点D是线段BC上一点(不含端点),过D作DE⊥AB于E,DF⊥AC于F.
(1)若△AEF外接圆的直径长为,求EF的值;
(2)求BC的取值范围;
(3)问点D在何处时,△DEF的面积最大?最大值为多少?
2018-2019学年上海市浦东新区华师大二附中高一(下)期中数学试卷
参考答案与试题解析
一、填空题(每小题4分,共40分)
1.【解答】解:2019°=360°×5+219°,是第三象限角.
故答案为:三.
2.【解答】解:∵角α的终边经过点P(2,﹣3),则 x=2,y=﹣3,r=|OP|==,
∴sinα==,
故答案为:﹣.
3.【解答】解:tanα=2,则===.
故答案为:
4.【解答】解:根据函数y=,可得cosx≥0,可得 2kπ﹣≤x≤2kπ+(k∈Z),
故函数的定义域为[2kπ﹣,2kπ+],k∈Z,
故答案为:[2kπ﹣,2kπ+],k∈Z.
5.【解答】解:由,
得﹣cos,即cos,
∴sinα=,则tanα==.
∴=﹣cot()=﹣tanα=.
故答案为:.
6.【解答】解:若在第二象限,
∴cosα=﹣,
则=====2,
故答案为:2
7.【解答】解:方程5sinx=4+2cos2x可化为5sinx=4+2(1﹣2sin2x),
即4sin2x+5sinx﹣6=0,
解得sinx=,或sinx=﹣2(不合题意,舍去);
所以该方程的解集为{x|x=arcsin+2kπ,或x=π﹣arcsin+2kπ,k∈Z}.
故答案为:{x|x=arcsin+2kπ,或x=π﹣arcsin+2kπ,k∈Z}.
8.【解答】解:由,得2sinα=,
∴,则tanα=.
由tan==1,解得tan=(舍)或.
∴===.
故答案为:.
9.【解答】解:根据题意知,f(x)=sin(x),令x=则,y=≠0
∴①②错误;由三角函数的性质知③④正确;
故答案为③④.
10.【解答】解:7sin2B+3sin2C=2sin2A+2sinAsinBsinC,
由正弦定理可得:7b2+3c2=2a2+2bcsinA,
∴a2=,又a2=b2+c2﹣2bccosA,
∴=b2+c2﹣2bccosA,
化为:2(sinA﹣2cosA)==≥2=2,
当且仅当b=c时取等号.
即2sin(A﹣θ)≥2,其中tanθ=2,sinθ=,cosθ=.
即sin(A﹣θ)≥1,又sin(A﹣θ)≤1,
∴sin(A﹣θ)=1.
∴A﹣θ=+2kπ,即A=θ++2kπ,k∈N*.
∴sin(A+)=sin(θ+++2kπ)=cos(θ+)
=(cosθ﹣sinθ)=×(﹣)=﹣.
∴=cos()=sin(A+)=.
故答案为:﹣.
二、选择题(每小题4分,共16分)
11.【解答】解:α是第三象限的角,则α∈(2kπ+π,2kπ+),k∈Z,
所以∈(kπ+,kπ+),k∈Z;
所以可以是第一、第三、或第四象限角.
故选:B.
12.【解答】解:函数的反函数是y=﹣cosx,x∈[0,π],
故选:D.
13.【解答】解:将已知等式2acosB=c,利用正弦定理化简得:2sinAcosB=sinC,
∵sinC=sin(A+B)=sinAcosB+cosAsinB,
∴2sinAcosB=sinAcosB+cosAsinB,即sinAcosB﹣cosAsinB=sin(A﹣B)=0,
∵A与B都为△ABC的内角,
∴A﹣B=0,即A=B,
已知第二个等式变形得:sinAsinB(2﹣cosC)=(1﹣cosC)+=1﹣cosC,
﹣[cos(A+B)﹣cos(A﹣B)](2﹣cosC)=1﹣cosC,
∴﹣(﹣cosC﹣1)(2﹣cosC)=1﹣cosC,
即(cosC+1)(2﹣cosC)=2﹣cosC,
整理得:cos2C﹣2cosC=0,即cosC(cosC﹣2)=0,
∴cosC=0或cosC=2(舍去),
∴C=90°,
则△ABC为等腰直角三角形.
故选:C.
14.【解答】解:由函数f(x)=cos(3x+φ)满足f(x)≤f(1)恒成立,
得函数f(x)的图象关于直线x=1对称,
即函数f(x+1)一定为偶函数,
故选:D.
三、解答题(共44分)
15.【解答】解:(1)∵,∴平方得sin2α+2sinαcosα+cos2α=,
得2sinαcosα=﹣1=﹣,
得sinαcosα=﹣.
(2)若α为第二象限的角,sinα>0,cosα<0,
则=+===﹣.
16.【解答】解:(1)由题意有:A=2,T=π,即ω==2,
由当x=时,函数f(x)取最大值,即2×+φ=2k,解得φ=2kπ,又0<φ,所以φ=,
即f(x)=2sin(2x+),
令2kπ≤2x+,得:k,(k∈Z)
故函数f(x)的解析式为:f(x)=2sin(2x+).
函数f(x)的单调递增区间为:[kπ,k](k∈Z).
(2)当,
则2x+∈[,],
所以2sin(2x+)∈[1,2],
故函数f(x)的最大值为2,最小值为1.
17.【解答】(本题满分为14分)
解:(1)由图知T=12=,∴ω=,…(1分)
A+b=5,b﹣A=3,可得:A=1,b=4,…(3分)
∴f(t)=sin(x+φ)+4,
代入(0,5),得φ=+2kπ,
又0<φ<π,
∴φ=…(5分)
即f(t)=sin(t+)+4,…(6分)
(2)设乙投产持续时间为t小时,则甲的投产持续时间为(t+m)小时,
由诱导公式,企业乙用电负荷量随持续时间t变化的关系式为:f(t)=cost+4;
同理,企业甲用电负荷量变化关系式为:f(t+m)=cos(t+m)+4;
两企业用电负荷量之和f(t+m)+f(t)=cos(t+m)+cost+8(t≥0);﹣﹣﹣﹣﹣﹣(8分)
依题意,有f(t+m)+f(t)=cos(t+m)+cost+8≤9恒成立,
即cos (t+m)+cos t≤1恒成立,
展开有:(cos m+1)cost﹣sinmsint≤1恒成立,﹣﹣﹣﹣﹣﹣(10分)
∵(cos m+1)cos t﹣sin msin t=Acos(t+?),
(其中,A=,cos?=;sin?=);
∴A=≤1,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)
整理得到:cos m≤﹣,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)
依据余弦函数图象得:+2kπ≤m≤+2kπ,(k∈Z),
即12k+4≤m≤12+8,取k=0得:4≤m≤8
∴m的最小值为4.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)
18.【解答】解:(1)∵在锐角△ABC中,,∴sinA=,
∵bc?,
∴bc=13,
∵△AEF外接圆的直径长为,
由正弦定理可得,==,
∴EF=3;
(2)在△ABC中,由余弦定理得,
BC2=b2+c2﹣2bccosA
=b2+c2﹣10≥2bc﹣10=16,
当且仅当b=c=时取等号,
∴BC≥4;
BC的取值范围:[4,+);
(3)设S△ABD=x,则S△ADC=6﹣x,
∵,
∴AB?AC=,
∵DE⊥AB于E,DF⊥AC于F,
∴,,
∴,,
∵
=
=
=﹣,
∴当x=3时,S△EDF的最大值为,.
∴当x=3时,三角形ABD与三角形ADC面积相等
∴D为BC的中点,
∴当D为BC的中点时,△DEF的面积最大,最大值为.△
同课章节目录
