26.2.3 求二次函数的表达式 课件 (23张PPT)
文档属性
| 名称 | 26.2.3 求二次函数的表达式 课件 (23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 00:00:00 | ||
图片预览







文档简介
课件23张PPT。第26章 二次函数26.2 二次函数的图象与性质求二次函数的表达式1课堂讲解用一般式(三点式)确定二次函数表达式
用顶点式确定二次函数表达式
用交点式确定二次函数表达式2课时流程逐点
导讲练课堂小结作业提升1. 一次函数的表达式是什么?如何求出它的表达式?
一次函数的表达式y=kx+b,只需知道一次函数图象上
两个点的坐标,利用待定系数法求出系数k、b.
2. 已知二次函数图象上的几个点的坐标,可以求出这个
二次函数的表达式?1知识点知1-导用一般式(三点式)确定二次函数表达式 求二次函数y=ax2+bx+c的表达式,关键是求出a、b、
c的值.由已知条件(如二次函数图象上的三个点的坐标)
可以列出关于a、b、c的三元一次方程组,求出三个待定
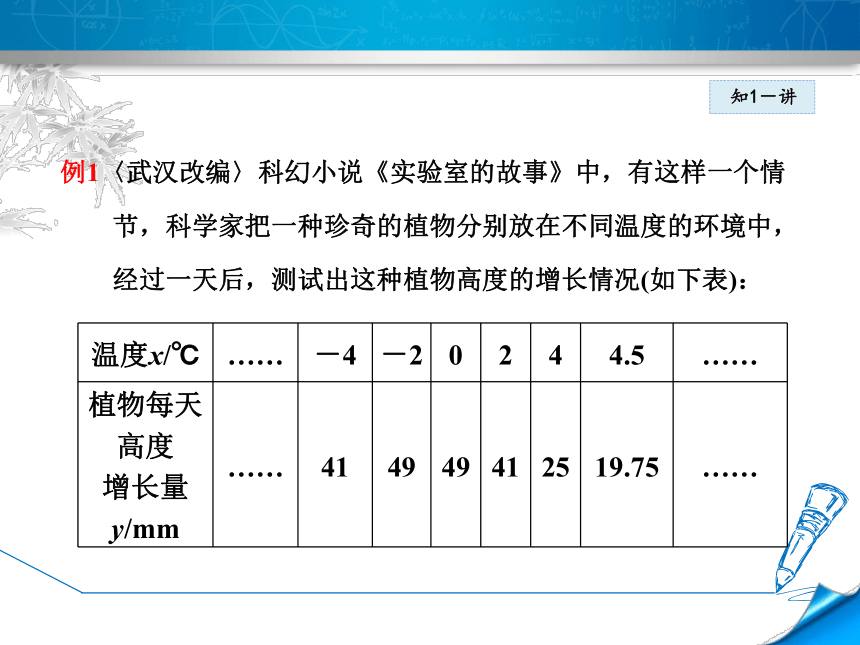
系数a、b、c就可以写出二次函数的表达式.知1-讲例1〈武汉改编〉科幻小说《实验室的故事》中,有这样一个情
节,科学家把一种珍奇的植物分别放在不同温度的环境中,
经过一天后,测试出这种植物高度的增长情况(如下表):知1-讲 由这些数据,科学家推测出植物每天高度增长量y是温度x
的函数,且这种函数是一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说
明不选择另一种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量
的总和超过250 mm,那么实验室的温度x应该在哪个范围内
选择?请直接写出结果.知1-讲(1)选择二次函数,设y=ax2+bx+c,
由题意得 解得
∴y关于x的函数关系式是y=-x2-2x+49.
不选另外一个函数的理由:点(-4,41),(-2,49),
(2,41)等不在同一直线上,
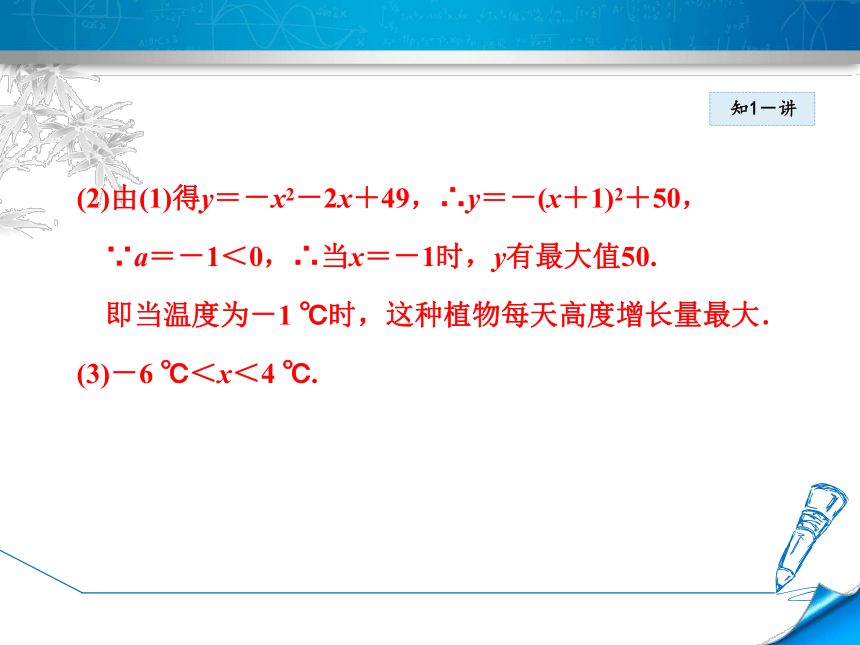
∴y不是x的一次函数.解:知1-讲(2)由(1)得y=-x2-2x+49,∴y=-(x+1)2+50,
∵a=-1<0,∴当x=-1时,y有最大值50.
即当温度为-1 ℃时,这种植物每天高度增长量最大.
(3)-6 ℃<x<4 ℃.知1-讲 已知抛物线过三点,求其表达式,可采用一般式;
而用一般式求待定系数要经历以下三步:
第一步:设一般式y=ax2+bx+c;
第二步:将三点的坐标分别代入一般式中,组成一个三
元一次方程组;
第三步:解方程组即可求出a,b,c的值.知1-练(中考·宁波)如图,已知二次函数y=ax2+bx+c的图象
过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的表达式;
(2)设二次函数的图象与x轴
的另一个交点为D,求点
D的坐标;
(3)在同一坐标系中画出直线
y=x+1,并写出当x在什
么范围内时,一次函数的值大于二次函数的值.2知识点知2-讲用顶点式确定二次函数表达式 已知抛物线的顶点坐标、对称轴或函数的最值时,
通常运用顶点式y=a(x-h)2+k来确定二次函数的表
达式;知2-讲例2 已知一个二次函数图象的顶点坐标为
且经过点(-2,0).求该二次函数的表达式.
由于已知顶点坐标为 故可设顶点式
y=a(x-h)2+k,从而代入得y=a(x-1)2-
再将(-2,0)代入求出a的值.导引:知2-讲 设二次函数的表达式为y=a(x-h)2+k.
∵顶点坐标为
∴y=a(x-1)2-
把(-2,0)代入得:0=a·(-2-1)2-
解得a=
∴该二次函数的表达式为y= (x-1)2-
即y= x2-x-4.解:知2-讲设顶点式求二次函数的表达式,通常有以下三种情况:
①已知顶点坐标;
②已知对称轴或顶点的横坐标;
③已知二次函数的最大(小)值或顶点的纵坐标.1 求图象为下列抛物线的二次函数的表达式:
(1)抛物线的顶点在原点,且抛物线经过点(2, 8);
(2)抛物线的顶点坐标为(-1,-2),且抛物线经过
点(1, 10).知2-练(来自教材)3知识点知3-讲用交点式确定二次函数表达式 在解决与二次函数的图象和x轴交点坐标有关的问
题时,使用交点式较为方便。设函数表达式为y=a(x-
x1)(x-x2) ,找到函数图象与x轴的两个交点,分别记横
坐标为x1和x2,代入公式,再有一个在抛物线上的点的坐
标,即可求出a的值.知3-讲例3〈宁波〉如图,已知抛物线y=ax2+bx+c与x轴交于
点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的表达式和顶点坐标;
(2)请你写出一种平移的方
法,使平移后抛物线的
顶点落在直线y=-x上,
并写出平移后抛物线的
表达式.知3-讲(1)利用交点式得出y=a(x-1)·(x-3),进而求出a的值,
再利用配方法求出顶点坐标即可;
(2)根据左加右减得出抛物线的表达式为y=-x2,进而
得出答案.导引:知3-讲(1)∵抛物线与x轴交于点A(1,0),B(3,0),
∴可设抛物线表达式为y=a(x-1)(x-3),
把(0,-3)代入得:3a=-3,解得:a=-1,
故抛物线的表达式为y=-(x-1)(x-3),
即y=-x2+4x-3.
∵y=-x2+4x-3=-(x-2)2+1,
∴顶点坐标为(2,1).
(2)先向左平移2个单位,再向下平移1个单位,得到的
抛物线的表达式为y=-x2,平移后抛物线的顶点为
(0,0),落在直线y=-x上.解:知3-讲 此题主要考查了二次函数的图象的平移,顶点坐标
以及交点式求二次函数表达式,根据平移性质得出平移
后的表达式是解题关键.第(2)小题是一个开放题,平移
方法不唯一;只需将原顶点平移成横纵坐标互为相反数
即可.已知抛物线与x轴交点坐标求其表达式时,一般
采用二次函数的交点式.如图,已知两点A(-8,0),B(2,0),以AB为直径
的半圆与y轴正半轴交于点C,OC=4.求经过A、B、
C三点的抛物线的表达式.知3-练用待定系数法求二次函数的表达式通常有以下四种类型:
(1)已知抛物线上的三点坐标或已知对应的三组x、y的值,
通常运用一般式y=ax2+bx+c,代入得到关于a、b、
c的方程组求解;
(2)已知抛物线的顶点坐标、对称轴或函数的最值时,通
常运用顶点式y=a(x-h)2+k来确定二次函数的表达式;(3)已知抛物线与x轴的两个交点坐标时,通常运用交
点式y=a(x-x1)(x-x2)来确定二次函数的表达式;
(4)若一条抛物线是由另一条抛物线经过平移得到的,
则可根据平移的条件,先确定出二次项系数a的值,
再用待定系数法求出二次函数的表达式.
用顶点式确定二次函数表达式
用交点式确定二次函数表达式2课时流程逐点
导讲练课堂小结作业提升1. 一次函数的表达式是什么?如何求出它的表达式?
一次函数的表达式y=kx+b,只需知道一次函数图象上
两个点的坐标,利用待定系数法求出系数k、b.
2. 已知二次函数图象上的几个点的坐标,可以求出这个
二次函数的表达式?1知识点知1-导用一般式(三点式)确定二次函数表达式 求二次函数y=ax2+bx+c的表达式,关键是求出a、b、
c的值.由已知条件(如二次函数图象上的三个点的坐标)
可以列出关于a、b、c的三元一次方程组,求出三个待定
系数a、b、c就可以写出二次函数的表达式.知1-讲例1〈武汉改编〉科幻小说《实验室的故事》中,有这样一个情
节,科学家把一种珍奇的植物分别放在不同温度的环境中,
经过一天后,测试出这种植物高度的增长情况(如下表):知1-讲 由这些数据,科学家推测出植物每天高度增长量y是温度x
的函数,且这种函数是一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说
明不选择另一种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量
的总和超过250 mm,那么实验室的温度x应该在哪个范围内
选择?请直接写出结果.知1-讲(1)选择二次函数,设y=ax2+bx+c,
由题意得 解得
∴y关于x的函数关系式是y=-x2-2x+49.
不选另外一个函数的理由:点(-4,41),(-2,49),
(2,41)等不在同一直线上,
∴y不是x的一次函数.解:知1-讲(2)由(1)得y=-x2-2x+49,∴y=-(x+1)2+50,
∵a=-1<0,∴当x=-1时,y有最大值50.
即当温度为-1 ℃时,这种植物每天高度增长量最大.
(3)-6 ℃<x<4 ℃.知1-讲 已知抛物线过三点,求其表达式,可采用一般式;
而用一般式求待定系数要经历以下三步:
第一步:设一般式y=ax2+bx+c;
第二步:将三点的坐标分别代入一般式中,组成一个三
元一次方程组;
第三步:解方程组即可求出a,b,c的值.知1-练(中考·宁波)如图,已知二次函数y=ax2+bx+c的图象
过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的表达式;
(2)设二次函数的图象与x轴
的另一个交点为D,求点
D的坐标;
(3)在同一坐标系中画出直线
y=x+1,并写出当x在什
么范围内时,一次函数的值大于二次函数的值.2知识点知2-讲用顶点式确定二次函数表达式 已知抛物线的顶点坐标、对称轴或函数的最值时,
通常运用顶点式y=a(x-h)2+k来确定二次函数的表
达式;知2-讲例2 已知一个二次函数图象的顶点坐标为
且经过点(-2,0).求该二次函数的表达式.
由于已知顶点坐标为 故可设顶点式
y=a(x-h)2+k,从而代入得y=a(x-1)2-
再将(-2,0)代入求出a的值.导引:知2-讲 设二次函数的表达式为y=a(x-h)2+k.
∵顶点坐标为
∴y=a(x-1)2-
把(-2,0)代入得:0=a·(-2-1)2-
解得a=
∴该二次函数的表达式为y= (x-1)2-
即y= x2-x-4.解:知2-讲设顶点式求二次函数的表达式,通常有以下三种情况:
①已知顶点坐标;
②已知对称轴或顶点的横坐标;
③已知二次函数的最大(小)值或顶点的纵坐标.1 求图象为下列抛物线的二次函数的表达式:
(1)抛物线的顶点在原点,且抛物线经过点(2, 8);
(2)抛物线的顶点坐标为(-1,-2),且抛物线经过
点(1, 10).知2-练(来自教材)3知识点知3-讲用交点式确定二次函数表达式 在解决与二次函数的图象和x轴交点坐标有关的问
题时,使用交点式较为方便。设函数表达式为y=a(x-
x1)(x-x2) ,找到函数图象与x轴的两个交点,分别记横
坐标为x1和x2,代入公式,再有一个在抛物线上的点的坐
标,即可求出a的值.知3-讲例3〈宁波〉如图,已知抛物线y=ax2+bx+c与x轴交于
点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的表达式和顶点坐标;
(2)请你写出一种平移的方
法,使平移后抛物线的
顶点落在直线y=-x上,
并写出平移后抛物线的
表达式.知3-讲(1)利用交点式得出y=a(x-1)·(x-3),进而求出a的值,
再利用配方法求出顶点坐标即可;
(2)根据左加右减得出抛物线的表达式为y=-x2,进而
得出答案.导引:知3-讲(1)∵抛物线与x轴交于点A(1,0),B(3,0),
∴可设抛物线表达式为y=a(x-1)(x-3),
把(0,-3)代入得:3a=-3,解得:a=-1,
故抛物线的表达式为y=-(x-1)(x-3),
即y=-x2+4x-3.
∵y=-x2+4x-3=-(x-2)2+1,
∴顶点坐标为(2,1).
(2)先向左平移2个单位,再向下平移1个单位,得到的
抛物线的表达式为y=-x2,平移后抛物线的顶点为
(0,0),落在直线y=-x上.解:知3-讲 此题主要考查了二次函数的图象的平移,顶点坐标
以及交点式求二次函数表达式,根据平移性质得出平移
后的表达式是解题关键.第(2)小题是一个开放题,平移
方法不唯一;只需将原顶点平移成横纵坐标互为相反数
即可.已知抛物线与x轴交点坐标求其表达式时,一般
采用二次函数的交点式.如图,已知两点A(-8,0),B(2,0),以AB为直径
的半圆与y轴正半轴交于点C,OC=4.求经过A、B、
C三点的抛物线的表达式.知3-练用待定系数法求二次函数的表达式通常有以下四种类型:
(1)已知抛物线上的三点坐标或已知对应的三组x、y的值,
通常运用一般式y=ax2+bx+c,代入得到关于a、b、
c的方程组求解;
(2)已知抛物线的顶点坐标、对称轴或函数的最值时,通
常运用顶点式y=a(x-h)2+k来确定二次函数的表达式;(3)已知抛物线与x轴的两个交点坐标时,通常运用交
点式y=a(x-x1)(x-x2)来确定二次函数的表达式;
(4)若一条抛物线是由另一条抛物线经过平移得到的,
则可根据平移的条件,先确定出二次项系数a的值,
再用待定系数法求出二次函数的表达式.
