26.2 二次函数的图象与性质 复习课件 (21张PPT)
文档属性
| 名称 | 26.2 二次函数的图象与性质 复习课件 (21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 296.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 17:02:51 | ||
图片预览




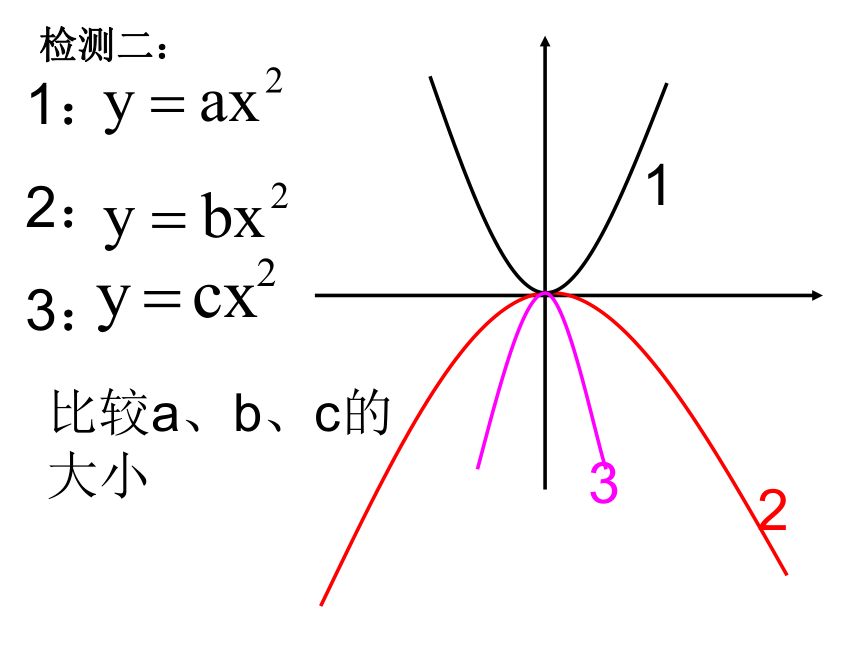



文档简介
课件21张PPT。二次函数的图象和性质(复习) 一、二次函数的定义 1.定义:一般地,形如 y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.2.定义要点:
(1)关于x的代数式一定是整式,a,b,c为常数,且a≠0.
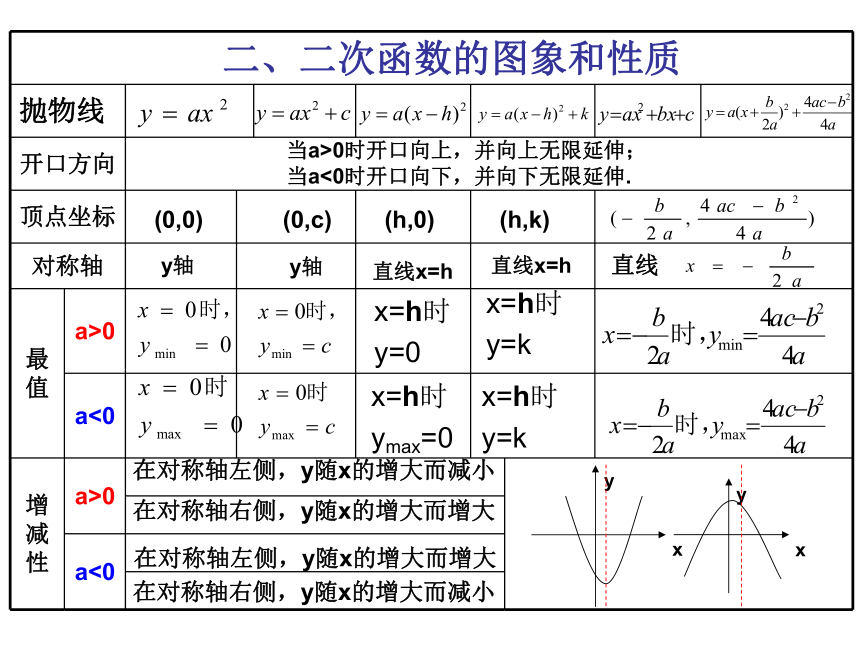
(2)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项.如: y=-x2, y=2x2-4x+3 , y=100-5x2,y=-2x2+5x-3 等等都是二次函数。二、二次函数的图象和性质当a>0时开口向上,并向上无限延伸;
当a<0时开口向下,并向下无限延伸.(0,0)(0,c)(h,0)(h,k)y轴在对称轴左侧,y随x的增大而减小在对称轴右侧,y随x的增大而增大在对称轴左侧,y随x的增大而增大在对称轴右侧,y随x的增大而减小y轴直线x=h直线x=hx=h时
y=0x=h时
ymax=0x=h时
y=kx=h时
y=k二次函数y=ax2+bx+c(a≠0)的系数a,b,c与图象的关系a决定开口方向及大小:a>0时,开口向上,a<0时,开口向下 a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴c决定抛物线与y轴的交点:c>0时抛物线交于y轴的正半轴
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴①②由①,得:由②,得:∴解:根据题意,得-1检测一:相信自己,你就能成功!1:
2:
3:123比较a、b、c的大小检测二:
2、抛物线y = x 2+3的开口方向向 ,对称轴是 ,顶点坐标是 ,是由抛物线y = x 2向 平移 个单位得到的;上直线X=0(0,3) 上3
3、y = - 2(x+3) 2的开口向___
对称轴是 ,顶点坐标
是 。
下直线X=-3(-3,0)2.抛物线y= (x-2)2-3与y轴
的交点坐标是_ ______.(0,-2)努力的你最可爱
5、下列关于抛物线 的说法中,正确的是( )
A.开口向下 B.对称轴是直线x=1
C.与x轴有两个交点
D.顶点坐标是(-1,0)D检测三:
1、若抛物线y = a (x+m) 2+n开口向下,顶点在第四象限,则
a 0, m 0, n 0。 〈〈〈 函数 的开口方向 ,
顶点坐标是 ,对称轴是 .解:∴ 顶点坐标为:对称轴是:向上检测七某二次函数满足下列表格中的x,y的值:
则该二次函数图象的对称轴是_________,
顶点坐标是_______.直线X=1(1,0)已知二次函数y=ax2+bx+c的图象经过点(1,-2),则a+b+c的值是 。
-2
二次函数 的图象向右平移3个单位,再向上平移1个单位,得到的图象的关系式是____________。 已知函数 ,设自变量的值分别为x1,x2,x3,且-3< x1< x2A.y3>y2>y1 B.y1>y3>y2 C.y2所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0
C、a<0,b<0,c>0 D、a<0,b<0,c<0 Bo检测四:C 3、二次函数y=ax2+bx+c(a≠0)的图象如上图所示,那么下列判断正确的有(填序号)
.
① abc>0, ② 4a-2b+c<0, ③ 2a+b>0, ④ a+b+c<0,⑤ a-b+c>0, ⑥ 4a+2b+c<0, ③②-1-2o12归纳小结、总结反思: (1)、通过本节课的复习,你有哪些收获?
(2)、本节课你认为自己解决的最好的问题是什么?
(3)、本节课还有哪些内容是你仍未听明白的?
(4)、在今后的学习中,你还要注意些什么??抛物线不仅拥有美丽的弧线,
她还赋予二次函数丰富的内涵!数形结合
(1)关于x的代数式一定是整式,a,b,c为常数,且a≠0.
(2)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项.如: y=-x2, y=2x2-4x+3 , y=100-5x2,y=-2x2+5x-3 等等都是二次函数。二、二次函数的图象和性质当a>0时开口向上,并向上无限延伸;
当a<0时开口向下,并向下无限延伸.(0,0)(0,c)(h,0)(h,k)y轴在对称轴左侧,y随x的增大而减小在对称轴右侧,y随x的增大而增大在对称轴左侧,y随x的增大而增大在对称轴右侧,y随x的增大而减小y轴直线x=h直线x=hx=h时
y=0x=h时
ymax=0x=h时
y=kx=h时
y=k二次函数y=ax2+bx+c(a≠0)的系数a,b,c与图象的关系a决定开口方向及大小:a>0时,开口向上,a<0时,开口向下 a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴c决定抛物线与y轴的交点:c>0时抛物线交于y轴的正半轴
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴①②由①,得:由②,得:∴解:根据题意,得-1检测一:相信自己,你就能成功!1:
2:
3:123比较a、b、c的大小检测二:
2、抛物线y = x 2+3的开口方向向 ,对称轴是 ,顶点坐标是 ,是由抛物线y = x 2向 平移 个单位得到的;上直线X=0(0,3) 上3
3、y = - 2(x+3) 2的开口向___
对称轴是 ,顶点坐标
是 。
下直线X=-3(-3,0)2.抛物线y= (x-2)2-3与y轴
的交点坐标是_ ______.(0,-2)努力的你最可爱
5、下列关于抛物线 的说法中,正确的是( )
A.开口向下 B.对称轴是直线x=1
C.与x轴有两个交点
D.顶点坐标是(-1,0)D检测三:
1、若抛物线y = a (x+m) 2+n开口向下,顶点在第四象限,则
a 0, m 0, n 0。 〈〈〈 函数 的开口方向 ,
顶点坐标是 ,对称轴是 .解:∴ 顶点坐标为:对称轴是:向上检测七某二次函数满足下列表格中的x,y的值:
则该二次函数图象的对称轴是_________,
顶点坐标是_______.直线X=1(1,0)已知二次函数y=ax2+bx+c的图象经过点(1,-2),则a+b+c的值是 。
-2
二次函数 的图象向右平移3个单位,再向上平移1个单位,得到的图象的关系式是____________。 已知函数 ,设自变量的值分别为x1,x2,x3,且-3< x1< x2
A、a<0,b>0,c>0 B、a<0,b>0,c<0
C、a<0,b<0,c>0 D、a<0,b<0,c<0 Bo检测四:C 3、二次函数y=ax2+bx+c(a≠0)的图象如上图所示,那么下列判断正确的有(填序号)
.
① abc>0, ② 4a-2b+c<0, ③ 2a+b>0, ④ a+b+c<0,⑤ a-b+c>0, ⑥ 4a+2b+c<0, ③②-1-2o12归纳小结、总结反思: (1)、通过本节课的复习,你有哪些收获?
(2)、本节课你认为自己解决的最好的问题是什么?
(3)、本节课还有哪些内容是你仍未听明白的?
(4)、在今后的学习中,你还要注意些什么??抛物线不仅拥有美丽的弧线,
她还赋予二次函数丰富的内涵!数形结合
