2019年中考数学考前冲刺复习——相似三角形专题课件共30张PPT
文档属性
| 名称 | 2019年中考数学考前冲刺复习——相似三角形专题课件共30张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 732.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-05 13:03:59 | ||
图片预览






文档简介
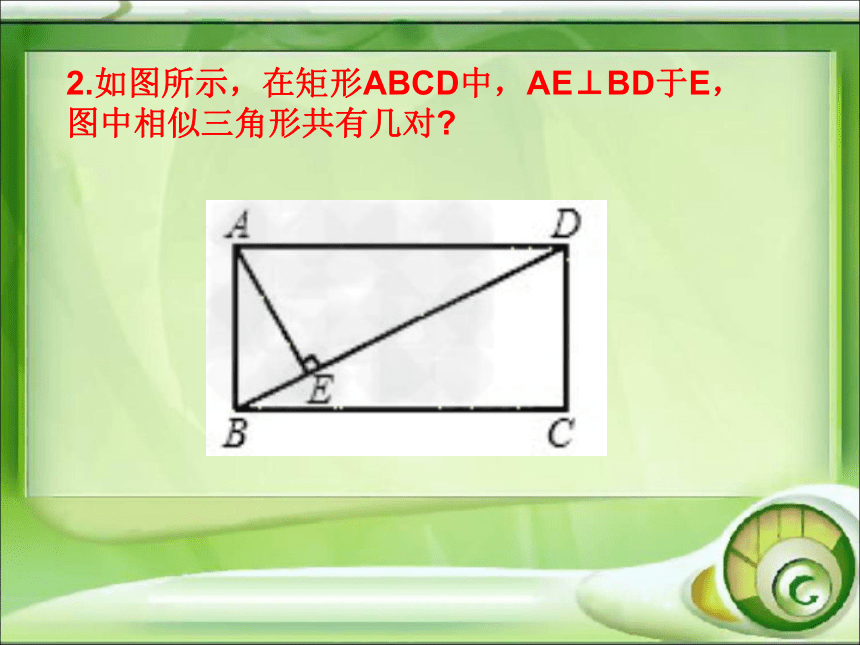
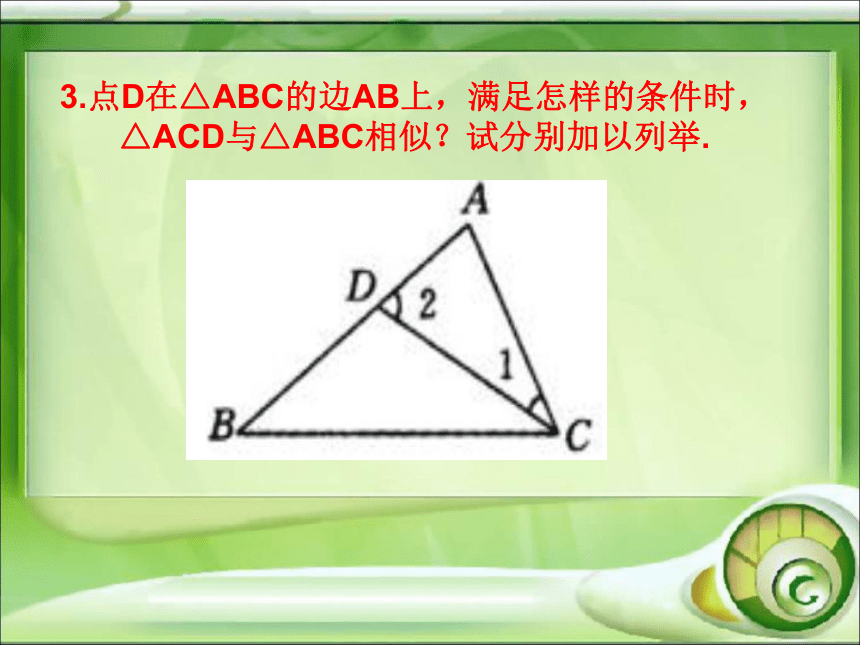
课件30张PPT。相似三角形复习中考数学冲刺复习考点一 相似三角形的定义 1.如图,AB‖CD,图中共有几对相似三角形? 2.如图所示,在矩形ABCD中,AE⊥BD于E,
图中相似三角形共有几对?3.点D在△ABC的边AB上,满足怎样的条件时,
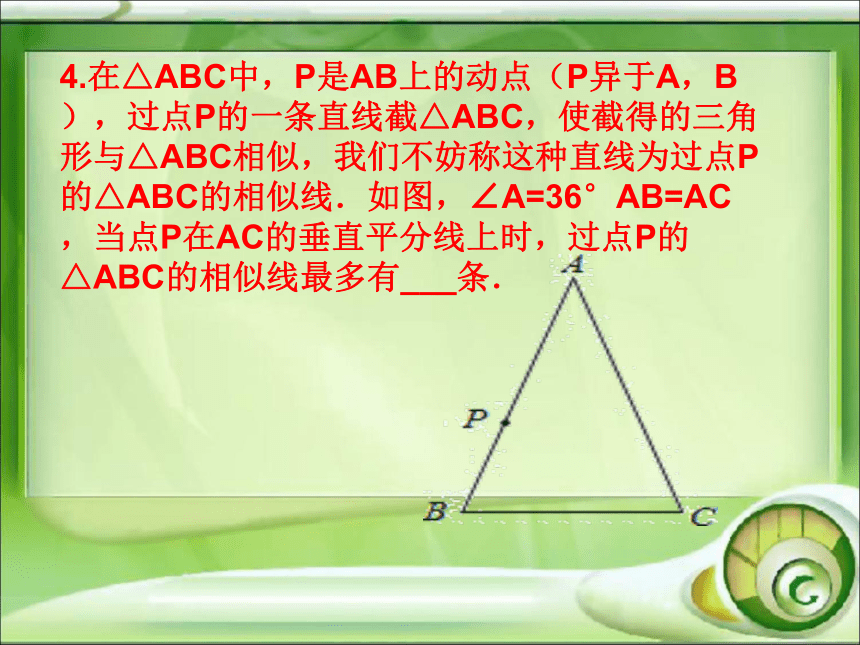
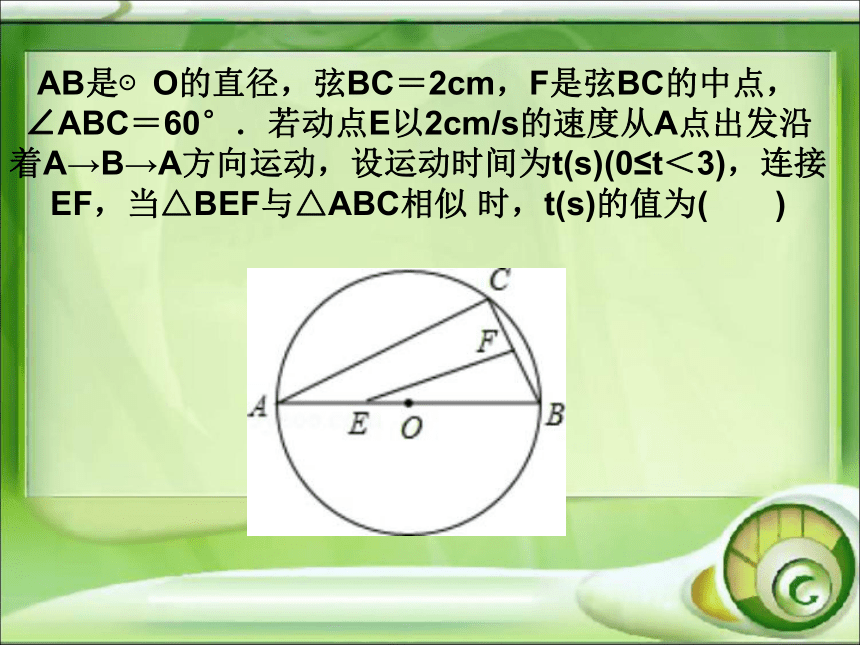
△ACD与△ABC相似?试分别加以列举. 4.在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有___条.考点二 相似三角形的判定 AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF与△ABC相似 时,t(s)的值为( )考点三 相似三角形的性质 巩固练习将一副三角尺如图所示叠放在一起,则的值是 .如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)(1)若△CEF与△ABC相似.①当AC=BC=2时,AD的长为 ;②当AC=3,BC=4时,AD的长为 ;(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.考点四 位似图形有关的概念与性质。 1.如果两个图形不仅是相似图形,而且每组对应顶点的连线都交于一点,那么这样的两个图形叫做位似图形。
2. 这个点叫做位似中心,这时的相似比又称为位似比.
注:
(1) 位似图形是相似图形的特例,位似图形不仅相似,而且对应顶点的连线相交于一点.
(2) 位似图形一定是相似图形,但相似图形不一定是位似图形.
(3) 位似图形的对应边互相平行或共线.
3.位似图形的性质: 位似图形上任意一对对应点到位似中心的距离之比等于相似比.
注:位似图形具有相似图形的所有性质.如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0)(8,2),(6,4)。已知△A1B1C1的两个顶点的坐标为(1,3),(2,5)。若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为 ▲ .中考真题2.将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A'C'D,如图(l)所示,将△A'C'D的顶点A'与点A重合,并绕点A按逆时针方向旋转,使点D、A(A')、B在同一条直线上,如图(2)所示,观察图(2)可知:与BC相等的线段是______,∠CAC'=______°问题探究
如图(3),在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论。
拓展延伸
如图(4),在△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H,若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由。探索发现:已知:在梯形ABCD中,CD∥AB,AD、BC的延长线相交于点E,AC、BD相交于点O,连接EO并延长交AB于点M,交CD于点N。(1)如图①,如果AD=BC,求证:直线EM是线段AB的垂直平分线;(2)如图②,如果AD≠BC,那么线段AM与BM是否相等?请说明理由。再 见
图中相似三角形共有几对?3.点D在△ABC的边AB上,满足怎样的条件时,
△ACD与△ABC相似?试分别加以列举. 4.在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有___条.考点二 相似三角形的判定 AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF与△ABC相似 时,t(s)的值为( )考点三 相似三角形的性质 巩固练习将一副三角尺如图所示叠放在一起,则的值是 .如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)(1)若△CEF与△ABC相似.①当AC=BC=2时,AD的长为 ;②当AC=3,BC=4时,AD的长为 ;(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.考点四 位似图形有关的概念与性质。 1.如果两个图形不仅是相似图形,而且每组对应顶点的连线都交于一点,那么这样的两个图形叫做位似图形。
2. 这个点叫做位似中心,这时的相似比又称为位似比.
注:
(1) 位似图形是相似图形的特例,位似图形不仅相似,而且对应顶点的连线相交于一点.
(2) 位似图形一定是相似图形,但相似图形不一定是位似图形.
(3) 位似图形的对应边互相平行或共线.
3.位似图形的性质: 位似图形上任意一对对应点到位似中心的距离之比等于相似比.
注:位似图形具有相似图形的所有性质.如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0)(8,2),(6,4)。已知△A1B1C1的两个顶点的坐标为(1,3),(2,5)。若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为 ▲ .中考真题2.将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A'C'D,如图(l)所示,将△A'C'D的顶点A'与点A重合,并绕点A按逆时针方向旋转,使点D、A(A')、B在同一条直线上,如图(2)所示,观察图(2)可知:与BC相等的线段是______,∠CAC'=______°问题探究
如图(3),在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论。
拓展延伸
如图(4),在△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H,若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由。探索发现:已知:在梯形ABCD中,CD∥AB,AD、BC的延长线相交于点E,AC、BD相交于点O,连接EO并延长交AB于点M,交CD于点N。(1)如图①,如果AD=BC,求证:直线EM是线段AB的垂直平分线;(2)如图②,如果AD≠BC,那么线段AM与BM是否相等?请说明理由。再 见
同课章节目录
