人教新课标A版 必修2 第二章 点、直线、平面之间的位置关系 2.1.1平面课件(40张)
文档属性
| 名称 | 人教新课标A版 必修2 第二章 点、直线、平面之间的位置关系 2.1.1平面课件(40张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-06 10:39:16 | ||
图片预览








文档简介
课件40张PPT。第二章 点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面一二三一、平面
1.生活中粉笔、电线杆等给我们以直线的形象;黑板、平整的操场、桌面、平静的湖面等则给我们以平面的印象,试举出更多例子.那么,平面的含义是什么呢?
提示:教室的地面,天花板等,几何里所说的“平面”就是从这样的一些物体中抽象出来的.但是,几何里的平面是无限延展的.
2.通常用什么图形来表示平面?
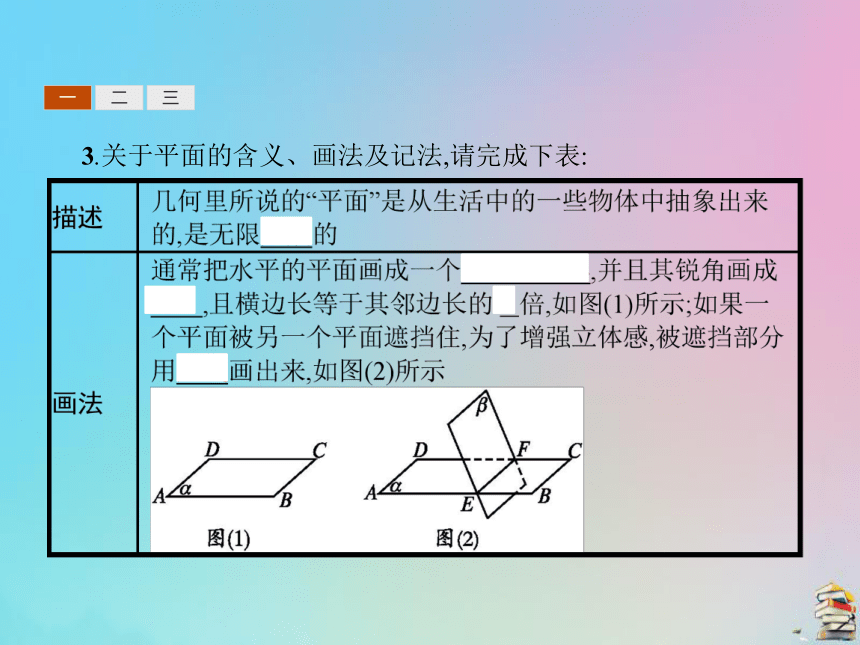
提示:一般用平行四边形.一二三3.关于平面的含义、画法及记法,请完成下表: 一二三一二三二、点、直线、平面之间的位置关系
1.平面α是由点组成的,直线l也是由点组成的,从集合的观点看,点P与直线l有何关系?点P与平面α有何关系?直线l与平面α呢?
提示:P∈l或P?l.P∈α或P?α.l?α或l?α.
2.若A∈a,a?α,能否推出A∈α?
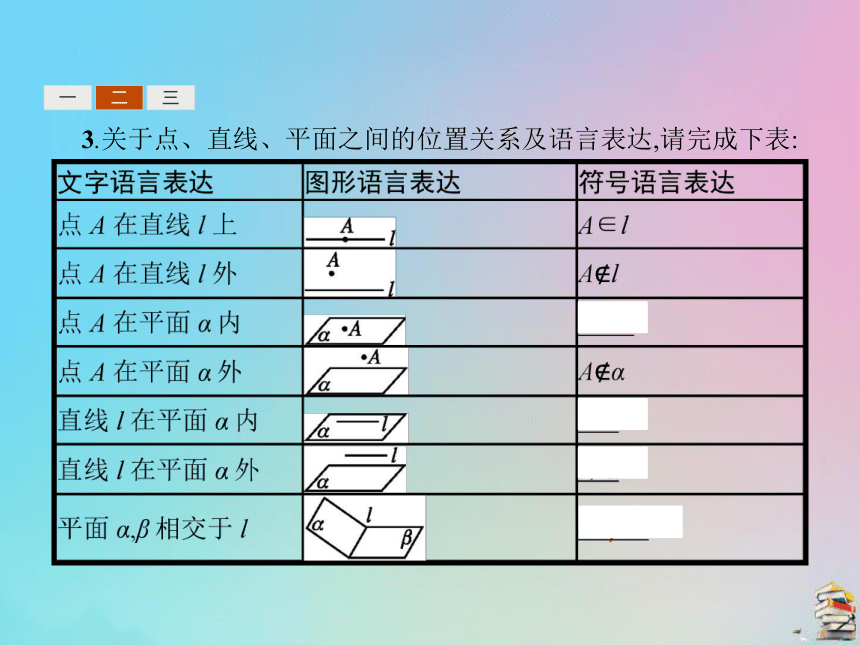
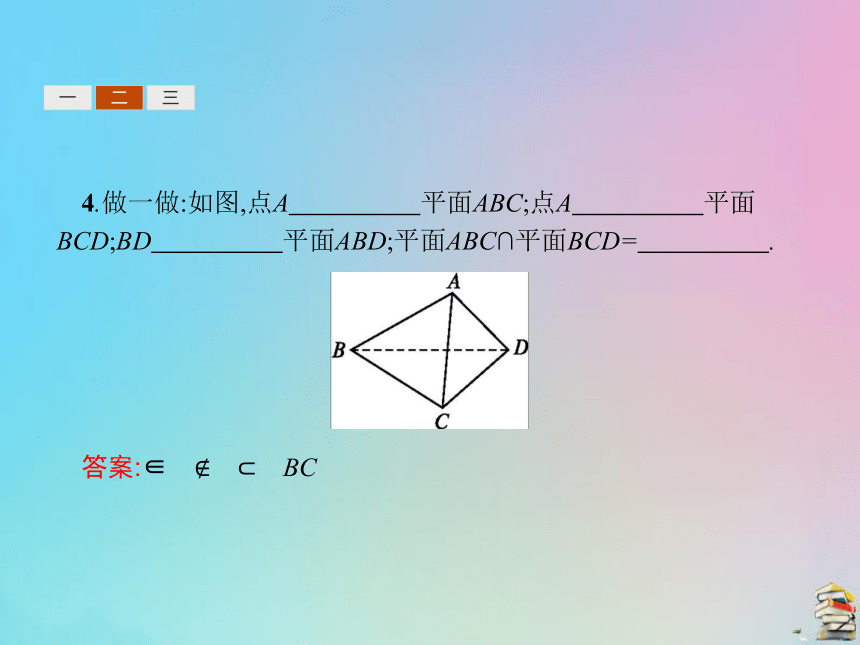
提示:由直线在平面内的定义可知,若A∈a,a?α,则A∈α.一二三3.关于点、直线、平面之间的位置关系及语言表达,请完成下表:一二三4.做一做:如图,点A 平面ABC;点A 平面BCD;BD 平面ABD;平面ABC∩平面BCD= .?
答案:∈ ? ? BC一二三三、平面的基本性质
1.现实生活中,我们可以做这样一个试验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.从该试验中我们能得到什么结论呢?
提示:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
2.观察下图,你能得出什么结论?
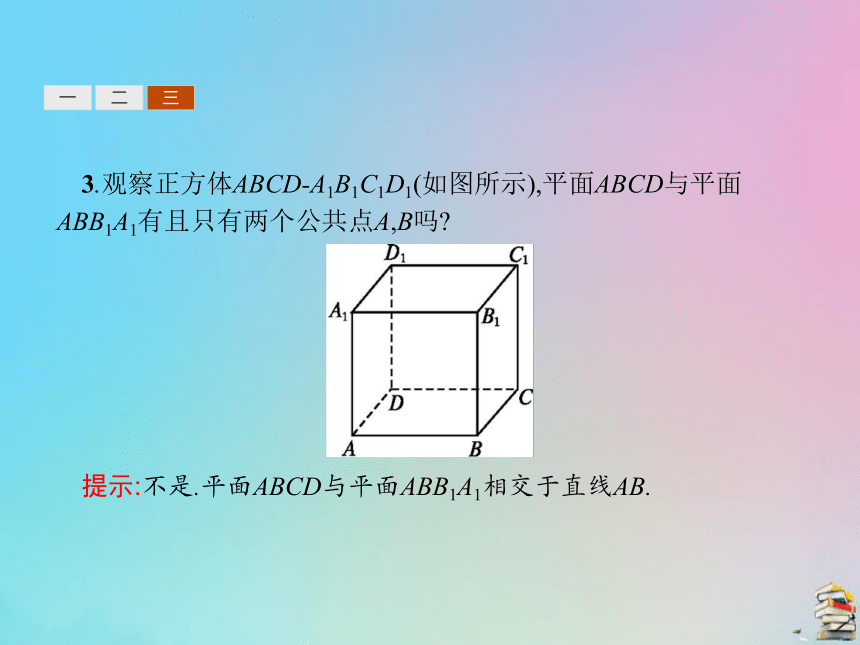
提示:不共线的三点可以确定一个平面.一二三3.观察正方体ABCD-A1B1C1D1(如图所示),平面ABCD与平面ABB1A1有且只有两个公共点A,B吗?
提示:不是.平面ABCD与平面ABB1A1相交于直线AB.一二三4.关于平面的基本性质,请完成下表: 一二三一二三5.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)三点可以确定一个平面.( )
(2)一条直线和一个点可以确定一个平面.( )
(3)四边形是平面图形.( )
(4)两条相交直线可以确定一个平面.( )
答案:(1)× (2)× (3)× (4)√探究一探究二探究三思想方法证明点、线共面
例1 证明:两两相交且不过同一点的三条直线共面.
已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
思路分析:先由l1与l2确定一个平面,再证明l3在这个平面内.也可以证明l1,l2确定的平面α与l2,l3确定的平面β重合.探究一探究二探究三思想方法证法一(纳入平面法)∵l1∩l2=A,∴l1和l2确定一个平面α.∵l2∩l3=B,∴B∈l2.又l2?α,∴B∈α.
同理可证C∈α.∵B∈l3,C∈l3,∴l3?α.
∴直线l1,l2,l3在同一平面内.
证法二(辅助平面法)∵l1∩l2=A,
∴l1,l2确定一个平面α.
∵l2∩l3=B,∴l2,l3确定一个平面β.
∵A∈l2,l2?α,∴A∈α.∵A∈l2,l2?β,∴A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
∴不共线的三个点A,B,C既在平面α内,又在平面β内.
∴平面α和β重合,即直线l1,l2,l3在同一平面内.探究一探究二探究三思想方法反思感悟证明多线共面的常用方法
(1)纳入法:先由部分点、线确定一个面,再证其余的点、线都在这个平面内.
(2)重合法:先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合.探究一探究二探究三思想方法延伸探究(1)把【例1】中的“不过同一点”删掉呢?这三条直线是否共面?
(2)把【例1】中“三条直线”改为“四条直线”呢?这四条直线是否共面?试证明你的结论.
解:(1)①不一定共面.
若三条直线两两相交,且过同一个点.
这三条直线在同一个平面内相交,如图.探究一探究二探究三思想方法这三条直线不共面.如图. ②若三条直线两两相交,且不过同一个点,由【例1】可知,这三条直线共面.探究一探究二探究三思想方法(2)共面.
已知:a,b,c,d四条直线两两相交,且不共点.
求证:a,b,c,d四线共面.
证明:①无三线共点情况,如图.
设a∩d=M,b∩d=N,c∩d=P,a∩b=Q,a∩c=R,b∩c=S.因为a∩d=M,所以a,d可确定一个平面α.
因为N∈d,Q∈a,所以N∈α,Q∈α,
所以NQ?α,即b?α.
同理,c?α,所以a,b,c,d共面.探究一探究二探究三思想方法②有三线共点的情况,如图.
设b,c,d三线相交于点K,与a分别交于N,P,M且K?a,
因为K?a,所以K和a确定一个平面,设为β.
因为N∈a,a?β,所以N∈β.所以NK?β,即b?β.
同理,c?β,d?β.
所以a,b,c,d共面.
由①②知,a,b,c,d共面.探究一探究二探究三思想方法证明多点共线
例2已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q,如图.
求证:P,Q,R三点共线.
思路分析:证明P,Q,R三点既在平面ABC内,也在平面α内,即得P,Q,R共线.也可以证明点Q既在平面APR内,也在平面α内,即点Q在平面APR与平面α的交线PR上.探究一探究二探究三思想方法证法一∵AB∩α=P,∴P∈AB,P∈平面α.
又AB?平面ABC,∴P∈平面ABC.
∴由公理3可知点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC与平面α的交线上,
∴P,Q,R三点共线.
证法二∵AP∩AR=A,
∴直线AP与直线AR确定平面APR.
又AB∩α=P,AC∩α=R,∴平面APR∩平面α=PR.
∵B∈平面APR,C∈平面APR,∴BC?平面APR.
∵Q∈BC,∴Q∈平面APR.又Q∈α,
∴Q∈PR,∴P,Q,R三点共线.探究一探究二探究三思想方法反思感悟证明多点共线的常用方法
证明多点共线通常利用公理3,通过证明点分别在两个平面内,证明点在相交平面的交线上;也可先选择其中两点确定一条直线,再证明其他点也在其上.探究一探究二探究三思想方法变式训练1如图所示,在正方体ABCD-A1B1C1D1中,设A1C∩平面ABC1D1=E.则B,E,D1三点的关系为 .(填“共线”或“不共线”)?探究一探究二探究三思想方法解析:如图所示,连接A1B,BD1,CD1.
∵A1C∩平面ABC1D1=E,
∴E∈A1C,E∈平面ABC1D1.
∵A1C?平面A1BCD1,
∴E∈平面A1BCD1.
∵平面A1BCD1∩平面ABC1D1=BD1,
∴E∈BD1,∴B,E,D1三点共线.
答案:共线探究一探究二探究三思想方法证明多线共点
例3如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE,D1F,DA三线交于一点.思路分析先证明两直线相交于P,再根据公理3证明点P落在第三条直线上.探究一探究二探究三思想方法证明如图,连接EF,D1C,A1B.
∵E为AB的中点,F为AA1的中点,
又∵A1B??D1C,
∴E,F,D1,C四点共面,
∴D1F与CE相交,设交点为P.
又D1F?平面A1D1DA,
CE?平面ABCD,
∴P为平面A1D1DA与平面ABCD的公共点.
又平面A1D1DA∩平面ABCD=DA,
根据公理3,可得P∈DA,
即CE,D1F,DA相交于一点.探究一探究二探究三思想方法反思感悟证明三线共点常用的方法
(1)先说明两条直线共面且交于一点,然后说明这个点在两个平面内.于是该点在这两个平面的交线上,从而得到三线共点.
(2)也可以说明a,b相交于一点A,b与c相交于一点B,再说明A,B是同一点,从而得到a,b,c三线共点.探究一探究二探究三思想方法变式训练2如图所示,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点,且四边形EFGH为梯形,HG∥EF,HG∶EF=1∶3.
求证:EH,BD,FG三条直线相交于同一点.探究一探究二探究三思想方法证明:延长EH,FG,不妨设EH∩FG=O,
∵HG∥EF,HG∶EF=1∶3,且EF≠GH,
∴EH,FG共面,且与FG不平行.
∵O∈EH,EH?平面ABD,
∴O∈平面ABD,
∵O∈FG,FG?平面BCD,
∴O∈平面BCD.
∵平面ABD∩平面BCD=BD,
∴O∈BD,
所以EH,BD,FG三条直线相交于同一点O.探究一探究二探究三思想方法转化思想在文字语言、图形语言与符号语言中的应用
典例 (1)用符号语言表示下列语句,并画出图形.
①三个平面α,β,γ相交于一点P,且平面α与平面β相交于PA,平面α与平面γ相交于PB,平面β与平面γ相交于PC;
②平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC.
(2)用文字语言和符号语言表示下图.【审题视角】 (1)根据条件,先适当确定其中的某一个平面,再根据点、线、面的位置关系,将其附着于固定平面上,注意图形的立体感,要将被遮挡部分用虚线表示.(2)用文字语言、符号语言表示一个图形时,应仔细观察图形有几个平面、几条直线且相互之间的位置关系如何.探究一探究二探究三思想方法解:(1)①符号语言.α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC;图形表示如图所示.
②符号语言.平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC;图形表示如图所示.
(2)文字语言.平面α内的直线m和n相交于点A;符号语言.m?α,n?α,且m∩n=A.探究一探究二探究三思想方法方法点睛用文字语言、符号语言表示一个图形时,首先仔细观察图形,有几个平面且位置关系如何,有几条直线且位置关系如何,图中的直线和平面的位置关系如何,有几点且在哪条直线或哪个平面上等,试着用文字语言表示,然后用符号语言表示.根据符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.探究一探究二探究三思想方法变式训练下列四个选项中的图形表示两个相交平面,其中画法正确的是( )
解析:选项A错误,理由是两平面的交线没画出,且被遮挡的部分未用虚线画出;选项B,C都错误,理由是被遮挡的部分未用虚线画出.D正确.
答案:D12341.如果直线a?平面α,直线b?平面α,M∈a,N∈b,M∈l,N∈l,则( )
A.l?α B.l?α
C.l∩α=M D.l∩α=N
解析:据公理1可知:直线l上两点M、N都在平面α内,所以l在平面α内.
答案:A12342.下列图形中,不一定是平面图形的是( )
A.三角形
B.平行四边形
C.梯形
D.四边相等的四边形
解析:利用公理2可知:三角形、平行四边形、梯形一定是平面图形,而四边相等的四边形不一定是平面图形.故选D.
答案:D12343.已知平面α∩平面β=l,点P∈α,P∈β,则点P与直线l的关系是 .?
答案:P∈l12344.不重合的三条直线,若相交于一点,最多能确定 个平面.?
解析:三条直线相交于一点,最多可确定3个平面,如图所示,直线a,b,c相交于点A,直线a,b确定平面α,直线b,c确定平面β,直线a,c确定平面γ,共3个平面.
答案:3
1.生活中粉笔、电线杆等给我们以直线的形象;黑板、平整的操场、桌面、平静的湖面等则给我们以平面的印象,试举出更多例子.那么,平面的含义是什么呢?
提示:教室的地面,天花板等,几何里所说的“平面”就是从这样的一些物体中抽象出来的.但是,几何里的平面是无限延展的.
2.通常用什么图形来表示平面?
提示:一般用平行四边形.一二三3.关于平面的含义、画法及记法,请完成下表: 一二三一二三二、点、直线、平面之间的位置关系
1.平面α是由点组成的,直线l也是由点组成的,从集合的观点看,点P与直线l有何关系?点P与平面α有何关系?直线l与平面α呢?
提示:P∈l或P?l.P∈α或P?α.l?α或l?α.
2.若A∈a,a?α,能否推出A∈α?
提示:由直线在平面内的定义可知,若A∈a,a?α,则A∈α.一二三3.关于点、直线、平面之间的位置关系及语言表达,请完成下表:一二三4.做一做:如图,点A 平面ABC;点A 平面BCD;BD 平面ABD;平面ABC∩平面BCD= .?
答案:∈ ? ? BC一二三三、平面的基本性质
1.现实生活中,我们可以做这样一个试验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.从该试验中我们能得到什么结论呢?
提示:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
2.观察下图,你能得出什么结论?
提示:不共线的三点可以确定一个平面.一二三3.观察正方体ABCD-A1B1C1D1(如图所示),平面ABCD与平面ABB1A1有且只有两个公共点A,B吗?
提示:不是.平面ABCD与平面ABB1A1相交于直线AB.一二三4.关于平面的基本性质,请完成下表: 一二三一二三5.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)三点可以确定一个平面.( )
(2)一条直线和一个点可以确定一个平面.( )
(3)四边形是平面图形.( )
(4)两条相交直线可以确定一个平面.( )
答案:(1)× (2)× (3)× (4)√探究一探究二探究三思想方法证明点、线共面
例1 证明:两两相交且不过同一点的三条直线共面.
已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
思路分析:先由l1与l2确定一个平面,再证明l3在这个平面内.也可以证明l1,l2确定的平面α与l2,l3确定的平面β重合.探究一探究二探究三思想方法证法一(纳入平面法)∵l1∩l2=A,∴l1和l2确定一个平面α.∵l2∩l3=B,∴B∈l2.又l2?α,∴B∈α.
同理可证C∈α.∵B∈l3,C∈l3,∴l3?α.
∴直线l1,l2,l3在同一平面内.
证法二(辅助平面法)∵l1∩l2=A,
∴l1,l2确定一个平面α.
∵l2∩l3=B,∴l2,l3确定一个平面β.
∵A∈l2,l2?α,∴A∈α.∵A∈l2,l2?β,∴A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
∴不共线的三个点A,B,C既在平面α内,又在平面β内.
∴平面α和β重合,即直线l1,l2,l3在同一平面内.探究一探究二探究三思想方法反思感悟证明多线共面的常用方法
(1)纳入法:先由部分点、线确定一个面,再证其余的点、线都在这个平面内.
(2)重合法:先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合.探究一探究二探究三思想方法延伸探究(1)把【例1】中的“不过同一点”删掉呢?这三条直线是否共面?
(2)把【例1】中“三条直线”改为“四条直线”呢?这四条直线是否共面?试证明你的结论.
解:(1)①不一定共面.
若三条直线两两相交,且过同一个点.
这三条直线在同一个平面内相交,如图.探究一探究二探究三思想方法这三条直线不共面.如图. ②若三条直线两两相交,且不过同一个点,由【例1】可知,这三条直线共面.探究一探究二探究三思想方法(2)共面.
已知:a,b,c,d四条直线两两相交,且不共点.
求证:a,b,c,d四线共面.
证明:①无三线共点情况,如图.
设a∩d=M,b∩d=N,c∩d=P,a∩b=Q,a∩c=R,b∩c=S.因为a∩d=M,所以a,d可确定一个平面α.
因为N∈d,Q∈a,所以N∈α,Q∈α,
所以NQ?α,即b?α.
同理,c?α,所以a,b,c,d共面.探究一探究二探究三思想方法②有三线共点的情况,如图.
设b,c,d三线相交于点K,与a分别交于N,P,M且K?a,
因为K?a,所以K和a确定一个平面,设为β.
因为N∈a,a?β,所以N∈β.所以NK?β,即b?β.
同理,c?β,d?β.
所以a,b,c,d共面.
由①②知,a,b,c,d共面.探究一探究二探究三思想方法证明多点共线
例2已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q,如图.
求证:P,Q,R三点共线.
思路分析:证明P,Q,R三点既在平面ABC内,也在平面α内,即得P,Q,R共线.也可以证明点Q既在平面APR内,也在平面α内,即点Q在平面APR与平面α的交线PR上.探究一探究二探究三思想方法证法一∵AB∩α=P,∴P∈AB,P∈平面α.
又AB?平面ABC,∴P∈平面ABC.
∴由公理3可知点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC与平面α的交线上,
∴P,Q,R三点共线.
证法二∵AP∩AR=A,
∴直线AP与直线AR确定平面APR.
又AB∩α=P,AC∩α=R,∴平面APR∩平面α=PR.
∵B∈平面APR,C∈平面APR,∴BC?平面APR.
∵Q∈BC,∴Q∈平面APR.又Q∈α,
∴Q∈PR,∴P,Q,R三点共线.探究一探究二探究三思想方法反思感悟证明多点共线的常用方法
证明多点共线通常利用公理3,通过证明点分别在两个平面内,证明点在相交平面的交线上;也可先选择其中两点确定一条直线,再证明其他点也在其上.探究一探究二探究三思想方法变式训练1如图所示,在正方体ABCD-A1B1C1D1中,设A1C∩平面ABC1D1=E.则B,E,D1三点的关系为 .(填“共线”或“不共线”)?探究一探究二探究三思想方法解析:如图所示,连接A1B,BD1,CD1.
∵A1C∩平面ABC1D1=E,
∴E∈A1C,E∈平面ABC1D1.
∵A1C?平面A1BCD1,
∴E∈平面A1BCD1.
∵平面A1BCD1∩平面ABC1D1=BD1,
∴E∈BD1,∴B,E,D1三点共线.
答案:共线探究一探究二探究三思想方法证明多线共点
例3如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE,D1F,DA三线交于一点.思路分析先证明两直线相交于P,再根据公理3证明点P落在第三条直线上.探究一探究二探究三思想方法证明如图,连接EF,D1C,A1B.
∵E为AB的中点,F为AA1的中点,
又∵A1B??D1C,
∴E,F,D1,C四点共面,
∴D1F与CE相交,设交点为P.
又D1F?平面A1D1DA,
CE?平面ABCD,
∴P为平面A1D1DA与平面ABCD的公共点.
又平面A1D1DA∩平面ABCD=DA,
根据公理3,可得P∈DA,
即CE,D1F,DA相交于一点.探究一探究二探究三思想方法反思感悟证明三线共点常用的方法
(1)先说明两条直线共面且交于一点,然后说明这个点在两个平面内.于是该点在这两个平面的交线上,从而得到三线共点.
(2)也可以说明a,b相交于一点A,b与c相交于一点B,再说明A,B是同一点,从而得到a,b,c三线共点.探究一探究二探究三思想方法变式训练2如图所示,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点,且四边形EFGH为梯形,HG∥EF,HG∶EF=1∶3.
求证:EH,BD,FG三条直线相交于同一点.探究一探究二探究三思想方法证明:延长EH,FG,不妨设EH∩FG=O,
∵HG∥EF,HG∶EF=1∶3,且EF≠GH,
∴EH,FG共面,且与FG不平行.
∵O∈EH,EH?平面ABD,
∴O∈平面ABD,
∵O∈FG,FG?平面BCD,
∴O∈平面BCD.
∵平面ABD∩平面BCD=BD,
∴O∈BD,
所以EH,BD,FG三条直线相交于同一点O.探究一探究二探究三思想方法转化思想在文字语言、图形语言与符号语言中的应用
典例 (1)用符号语言表示下列语句,并画出图形.
①三个平面α,β,γ相交于一点P,且平面α与平面β相交于PA,平面α与平面γ相交于PB,平面β与平面γ相交于PC;
②平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC.
(2)用文字语言和符号语言表示下图.【审题视角】 (1)根据条件,先适当确定其中的某一个平面,再根据点、线、面的位置关系,将其附着于固定平面上,注意图形的立体感,要将被遮挡部分用虚线表示.(2)用文字语言、符号语言表示一个图形时,应仔细观察图形有几个平面、几条直线且相互之间的位置关系如何.探究一探究二探究三思想方法解:(1)①符号语言.α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC;图形表示如图所示.
②符号语言.平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC;图形表示如图所示.
(2)文字语言.平面α内的直线m和n相交于点A;符号语言.m?α,n?α,且m∩n=A.探究一探究二探究三思想方法方法点睛用文字语言、符号语言表示一个图形时,首先仔细观察图形,有几个平面且位置关系如何,有几条直线且位置关系如何,图中的直线和平面的位置关系如何,有几点且在哪条直线或哪个平面上等,试着用文字语言表示,然后用符号语言表示.根据符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.探究一探究二探究三思想方法变式训练下列四个选项中的图形表示两个相交平面,其中画法正确的是( )
解析:选项A错误,理由是两平面的交线没画出,且被遮挡的部分未用虚线画出;选项B,C都错误,理由是被遮挡的部分未用虚线画出.D正确.
答案:D12341.如果直线a?平面α,直线b?平面α,M∈a,N∈b,M∈l,N∈l,则( )
A.l?α B.l?α
C.l∩α=M D.l∩α=N
解析:据公理1可知:直线l上两点M、N都在平面α内,所以l在平面α内.
答案:A12342.下列图形中,不一定是平面图形的是( )
A.三角形
B.平行四边形
C.梯形
D.四边相等的四边形
解析:利用公理2可知:三角形、平行四边形、梯形一定是平面图形,而四边相等的四边形不一定是平面图形.故选D.
答案:D12343.已知平面α∩平面β=l,点P∈α,P∈β,则点P与直线l的关系是 .?
答案:P∈l12344.不重合的三条直线,若相交于一点,最多能确定 个平面.?
解析:三条直线相交于一点,最多可确定3个平面,如图所示,直线a,b,c相交于点A,直线a,b确定平面α,直线b,c确定平面β,直线a,c确定平面γ,共3个平面.
答案:3
