人教新课标A版 必修2 第二章 点、直线、平面之间的位置关系 2.1.2空间中直线与直线之间的位置关系课件(35张)
文档属性
| 名称 | 人教新课标A版 必修2 第二章 点、直线、平面之间的位置关系 2.1.2空间中直线与直线之间的位置关系课件(35张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-06 10:40:16 | ||
图片预览









文档简介
课件35张PPT。2.1.2 空间中直线与直线之间的位置关系一二三四一、空间中两条直线的位置关系
1.同一平面内两条直线有几种位置关系?分别是什么关系?
提示:两种.分别是平行关系和相交关系.
2.观察长方体ABCD-A1B1C1D1,棱A1D1所在的直线与棱BB1所在的直线在同一个平面内吗?它们是什么关系?
提示:不在同一个平面内,它们是异面关系.
3.分别在两个平面内的两条直线是否一定异面?
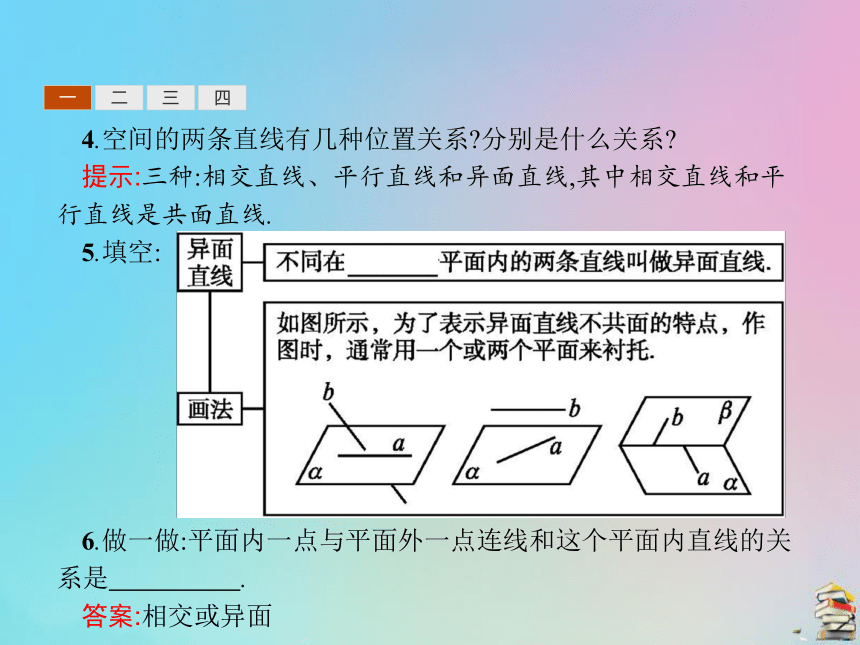
提示:不一定.它们可能异面,可能相交,也可能平行.一二三四4.空间的两条直线有几种位置关系?分别是什么关系?
提示:三种:相交直线、平行直线和异面直线,其中相交直线和平行直线是共面直线.
5.填空:6.做一做:平面内一点与平面外一点连线和这个平面内直线的关系是 .?
答案:相交或异面一二三四二、平行公理
1.观察长方体ABCD-A1B1C1D1,显然AB∥CD,CD∥C1D1,则AB与C1D1有何位置关系?
提示:AB∥C1D1.2.关于公理4,请完成下表: 一二三四3.做一做:
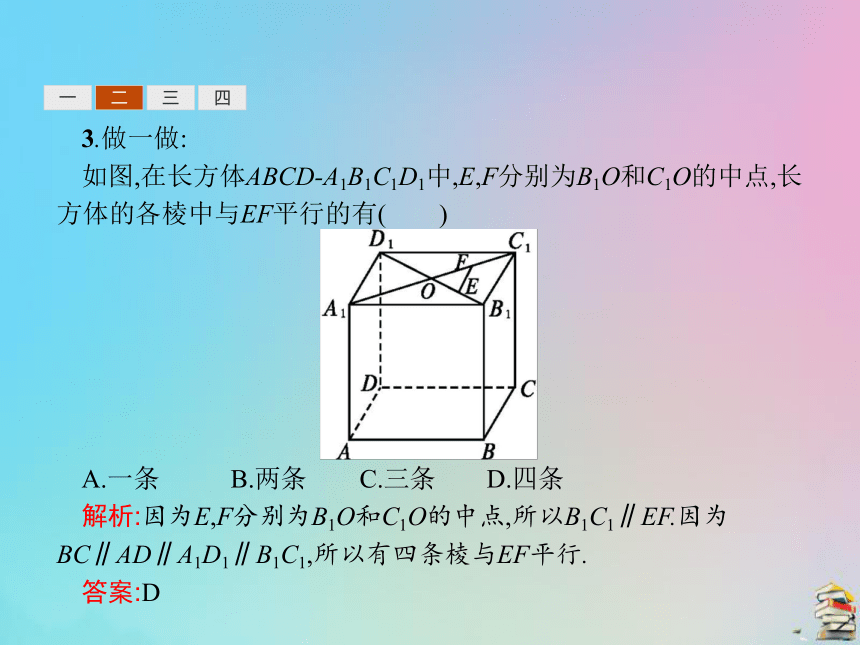
如图,在长方体ABCD-A1B1C1D1中,E,F分别为B1O和C1O的中点,长方体的各棱中与EF平行的有( )
A.一条 B.两条 C.三条 D.四条
解析:因为E,F分别为B1O和C1O的中点,所以B1C1∥EF.因为BC∥AD∥A1D1∥B1C1,所以有四条棱与EF平行.
答案:D一二三四三、等角定理
1.如图,在四棱柱ABCD-A'B'C'D'中,底面ABCD为菱形,∠ADC与∠A'D'C',∠ADC与∠A'B'C'的两边分别对应平行,这两组角的大小关系如何?
提示:∠ADC=∠A'D'C',∠ADC+∠A'B'C'=180°.
2.平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”,在空间中,该结论是否仍然成立?
提示:仍然成立.一二三四3.填空:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
4.做一做:已知∠BAC=30°,AB∥A'B',AC∥A'C',则∠B'A'C'=( )
A.30°
B.150°
C.30°或150°
D.大小无法确定
解析:当∠B'A'C'与∠BAC开口方向相同时,∠B'A'C'=30°;当∠B'A'C'与∠BAC开口方向相反时,∠B'A'C'=150°.
答案:C一二三四四、异面直线所成的角
1.在长方体A1B1C1D1-ABCD中,BC1∥AD1,则“直线BC1与直线BC所成的角”与“直线AD1与直线BC所成的角”是否相等?
提示:相等.
2.若两条相交直线a',b'所成的角为θ',则θ'的取值范围是什么?类似地,若两条异面直线a,b所成的角为θ,则θ的取值范围是什么?
提示:0°<θ'≤90°,0°<θ≤90°.一二三四3.关于两条异面直线所成的角(夹角),填写下表: 一二三四4.做一做:在正方体ABCD-A1B1C1D1中,∠BAE=25°,则异面直线AE与B1C1所成的角的大小为 .?
答案:65°探究一探究二探究三思维辨析空间两条直线位置关系的判定
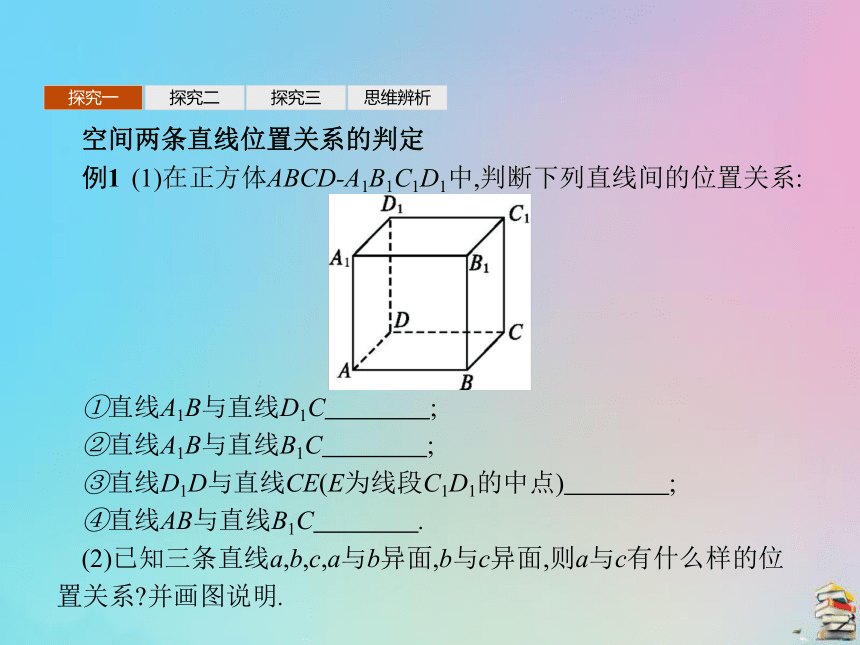
例1 (1)在正方体ABCD-A1B1C1D1中,判断下列直线间的位置关系:①直线A1B与直线D1C ;?
②直线A1B与直线B1C ;?
③直线D1D与直线CE(E为线段C1D1的中点) ;?
④直线AB与直线B1C .?
(2)已知三条直线a,b,c,a与b异面,b与c异面,则a与c有什么样的位置关系?并画图说明.探究一探究二探究三思维辨析思路分析:(1)
(2)根据异面直线的定义分析.
解:(1)①平行 ②异面 ③相交 ④异面
(2)直线a与c的位置关系有三种情况,如图所示.
直线a与c可能平行,如图①;可能相交,如图②;可能异面,如图③.探究一探究二探究三思维辨析反思感悟空间两条直线位置关系的判定方法:
(1)判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.
(2)判定两条直线是异面直线的方法:
①定义法:由定义判断两直线不可能在同一平面内;
②排除法(反证法):排除两直线共面(平行或相交);
③重要结论(判定定理法):连接平面内一点与平面外一点的直线和这个平面内不经过此点的直线是异面直线.如图,A?α,B∈α,l?α,B?l?AB与l是异面直线.探究一探究二探究三思维辨析延伸探究在本例的正方体中,所有与直线AB异面的棱所在的直线为 .?
答案:CC1,B1C1,DD1,A1D1探究一探究二探究三思维辨析平行公理、等角定理的应用
例2如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠B1M1C1=∠BMC.
思路分析:(1)通过公理4证明MM1∥BB1,且MM1=BB1;(2)由(1)知B1M1∥BM,同理证得C1M1∥CM,再由等角定理证得∠BMC=∠B1M1C1.也可以通过证明△BCM≌△B1C1M1证出∠BMC=∠B1M1C1.探究一探究二探究三思维辨析证明:(1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,
∴MM1??AA1.
又AA1??BB1,
∴MM1∥BB1,且MM1=BB1,
∴四边形BB1M1M为平行四边形.探究一探究二探究三思维辨析(2)(方法一)由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
由(1)同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.∴∠BMC=∠B1M1C1.
(方法二)由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
由(1)同理可得四边形CC1M1M为平行四边形,
∴C1M1=CM.
又B1C1=BC,
∴△B1C1M1≌△BCM,
∴∠B1M1C1=∠BMC.探究一探究二探究三思维辨析反思感悟公理4及等角定理的应用
判断两直线平行仍是立体几何中的一个重要组成部分,除了平面几何中常用的判断方法以外,公理4也是判断两直线平行的重要依据.
证明角相等,利用空间等角定理是常用的思考方法;另外也可以通过证明两个三角形全等或相似来证明两角相等.在应用等角定理时,应注意当两个角的两边分别对应平行且方向都相同或相反时,这两个角相等,否则这两个角互补.因此,在证明两个角相等时,只说明两个角的两边分别对应平行是不够的.探究一探究二探究三思维辨析变式训练 已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:
(1)四边形MNA1C1是梯形;(2)∠DNM=∠D1A1C1.
证明(1)如图,连接AC,
在△ACD中,∵M,N分别是CD,AD的中点,
∴MN是△ACD的中位线,∴MN∥AC,MN= AC.
由正方体的性质,得AC∥A1C1,AC=A1C1.
∴MN∥A1C1,且MN= A1C1,即MN≠A1C1,∴四边形MNA1C1是梯形.
(2)由(1)可知MN∥A1C1,又∵ND∥A1D1,
∴∠DNM与∠D1A1C1相等或互补.
而∠DNM与∠D1A1C1均是直角三角形的一个锐角,
∴∠DNM=∠D1A1C1.探究一探究二探究三思维辨析求异面直线所成的角
例3 如图,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小.
思路分析:先作出角,再证明角的两边分别与两异面直线平行,最后在三角形中求角.探究一探究二探究三思维辨析解法一如图(1),连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,则OG∥B1D,EF∥A1C1.
∴∠GOA1为异面直线DB1与EF所成的角或其补角.
∵GA1=GC1,O为A1C1的中点,
∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.探究一探究二探究三思维辨析解法二如图(2),连接A1D,取A1D的中点H,连接HE,则HE∥DB1,且HE= DB1.
于是∠HEF为异面直线DB1与EF所成的角或补角.取A1D1的中点I,连接IF,IH,则HI⊥IF,
∴HF2=HI2+IF2= ,
∴HF2=EF2+HE2,∴∠HEF=90°,
∴异面直线DB1与EF所成的角为90°.探究一探究二探究三思维辨析解法三如图(3),在原正方体的右侧补上一个全等的正方体,连接B1Q,则B1Q∥EF.
于是∠DB1Q为异面直线DB1与EF所成的角或其补角.
通过计算,不难得到:B1D2+B1Q2=DQ2,从而异面直线DB1与EF所成的角为90°.探究一探究二探究三思维辨析反思感悟(1)求两条异面直线所成角的一般步骤
①构造:恰当地选择一个点(线段的端点或中点),用平移法构造异面直线所成的角;
②证明:证明①中所作出的角就是所求异面直线所成的角或其补角;
③计算:通过解三角形等知识,求出①中所构造的角的大小;
④结论:假如所构造的角的大小为α,若0°<α≤90°,则α即为所求异面直线所成角的大小;若90°<α<180°,则180°-α即为所求.
(2)作异面直线所成角的常用方法
①直接平移法(可利用图中已有的平行线);
②中位线平移法;
③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).探究一探究二探究三思维辨析(2)作出异面直线所成的角,可通过多种方法平移产生,主要有三种方法:
①直接平移法(可利用图中已有的平行线);
②中位线平移法;
③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).探究一探究二探究三思维辨析延伸探究若把“直线DB1”换为“直线DC1”呢?
解:如图,连接A1C1,A1D.
在△A1B1C1中,A1E=EB1,C1F=FB1,所以EF∥A1C1.所以∠A1C1D为直线DC1与EF所成的角.
在△A1C1D中,A1D=DC1=A1C1,
所以∠A1C1D=60°,
所以直线DC1与EF所成的角等于60°.探究一探究二探究三思维辨析一题多解——判断两条直线异面
典例如图,空间四边形ABCD,AB≠AC,AE是△ABC的BC边上的高,DF是△BCD的BC边上的中线,求证:AE和DF是异面直线.
点拨:根据题意画出示意图,由题设条件可知点E,F不重合,需结合AE和DF的位置关系判断.探究一探究二探究三思维辨析证法一(定理法)
由题设条件可知点E、F不重合,设△BCD所在平面为α.
证法二(反证法)
若AE和DF不是异面直线,则AE和DF共面,设过AE、DF的平面为β.
(1)若E,F重合,则E是BC中点,AB=AC,这与题设AB≠AC相矛盾.
(2)若E,F不重合,
∵B∈EF,C∈EF,EF?β,∴BC?β.
∵A∈β,D∈β,
∴A、B、C、D四点共面,这与题设四边形ABCD是空间四边形相矛盾.
综上,AE和DF不是异面直线不成立.
故AE和DF是异面直线.探究一探究二探究三思维辨析方法总结 判断两条直线异面常用的方法:
(1)定义法,不同在任一平面内的两条直线;
(2)定理法,过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.
(3)推论法,一条直线上两点与另一条与它异面的直线上两点所连成的两条直线为异面直线.123451.空间两条直线a、b与直线l都成异面直线,则a、b的位置关系是( )
A.平行或相交 B.异面或平行
C.异面或相交 D.平行或异面或相交
解析:直线a、b与直线l都成异面直线,a与b之间并没有任何限制,所以a与b直线的位置关系所有情况都可能.
答案:D123452.直线a与直线b相交,直线c与直线b相交,则直线a与直线c的位置关系是( )
A.相交 B.平行
C.异面 D.以上都有可能
解析:如图所示,在长方体ABCD-A1B1C1D1中,AB与AA1相交,A1B1与AA1相交,AB∥A1B1;又AD与AA1相交,AB与AD相交;又A1D1与AA1相交,AB与A1D1异面.故选D.
答案:D123453.一个无盖的正方体盒子展开后的平面图如图所示,A,B,C是展开图上的三点,则在正方体盒子中,∠ABC的大小是( )
A.45°
B.30°
C.60°
D.90°
解析:将平面图形折叠,得立体图,如图所示,可得△ABC的各边均为正方形的面对角线长,所以△ABC为等边三角形,所以∠ABC的大小为60°.故选C.
答案:C123454.已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于 ( )
A.30° B.30°或150°
C.150° D.以上结论都不对
解析:∠ABC的两边与∠PQR的两边分别平行,但方向不能确定是否相同.∴∠PQR=30°或150°.
答案:B123455.如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.则四边形EFGH是 .?
解析:连接BD,因为EH是△ABD的中位线,∴EH∥FG,且EH=FG.
∴四边形EFGH是平行四边形.
答案:平行四边形
1.同一平面内两条直线有几种位置关系?分别是什么关系?
提示:两种.分别是平行关系和相交关系.
2.观察长方体ABCD-A1B1C1D1,棱A1D1所在的直线与棱BB1所在的直线在同一个平面内吗?它们是什么关系?
提示:不在同一个平面内,它们是异面关系.
3.分别在两个平面内的两条直线是否一定异面?
提示:不一定.它们可能异面,可能相交,也可能平行.一二三四4.空间的两条直线有几种位置关系?分别是什么关系?
提示:三种:相交直线、平行直线和异面直线,其中相交直线和平行直线是共面直线.
5.填空:6.做一做:平面内一点与平面外一点连线和这个平面内直线的关系是 .?
答案:相交或异面一二三四二、平行公理
1.观察长方体ABCD-A1B1C1D1,显然AB∥CD,CD∥C1D1,则AB与C1D1有何位置关系?
提示:AB∥C1D1.2.关于公理4,请完成下表: 一二三四3.做一做:
如图,在长方体ABCD-A1B1C1D1中,E,F分别为B1O和C1O的中点,长方体的各棱中与EF平行的有( )
A.一条 B.两条 C.三条 D.四条
解析:因为E,F分别为B1O和C1O的中点,所以B1C1∥EF.因为BC∥AD∥A1D1∥B1C1,所以有四条棱与EF平行.
答案:D一二三四三、等角定理
1.如图,在四棱柱ABCD-A'B'C'D'中,底面ABCD为菱形,∠ADC与∠A'D'C',∠ADC与∠A'B'C'的两边分别对应平行,这两组角的大小关系如何?
提示:∠ADC=∠A'D'C',∠ADC+∠A'B'C'=180°.
2.平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”,在空间中,该结论是否仍然成立?
提示:仍然成立.一二三四3.填空:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
4.做一做:已知∠BAC=30°,AB∥A'B',AC∥A'C',则∠B'A'C'=( )
A.30°
B.150°
C.30°或150°
D.大小无法确定
解析:当∠B'A'C'与∠BAC开口方向相同时,∠B'A'C'=30°;当∠B'A'C'与∠BAC开口方向相反时,∠B'A'C'=150°.
答案:C一二三四四、异面直线所成的角
1.在长方体A1B1C1D1-ABCD中,BC1∥AD1,则“直线BC1与直线BC所成的角”与“直线AD1与直线BC所成的角”是否相等?
提示:相等.
2.若两条相交直线a',b'所成的角为θ',则θ'的取值范围是什么?类似地,若两条异面直线a,b所成的角为θ,则θ的取值范围是什么?
提示:0°<θ'≤90°,0°<θ≤90°.一二三四3.关于两条异面直线所成的角(夹角),填写下表: 一二三四4.做一做:在正方体ABCD-A1B1C1D1中,∠BAE=25°,则异面直线AE与B1C1所成的角的大小为 .?
答案:65°探究一探究二探究三思维辨析空间两条直线位置关系的判定
例1 (1)在正方体ABCD-A1B1C1D1中,判断下列直线间的位置关系:①直线A1B与直线D1C ;?
②直线A1B与直线B1C ;?
③直线D1D与直线CE(E为线段C1D1的中点) ;?
④直线AB与直线B1C .?
(2)已知三条直线a,b,c,a与b异面,b与c异面,则a与c有什么样的位置关系?并画图说明.探究一探究二探究三思维辨析思路分析:(1)
(2)根据异面直线的定义分析.
解:(1)①平行 ②异面 ③相交 ④异面
(2)直线a与c的位置关系有三种情况,如图所示.
直线a与c可能平行,如图①;可能相交,如图②;可能异面,如图③.探究一探究二探究三思维辨析反思感悟空间两条直线位置关系的判定方法:
(1)判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.
(2)判定两条直线是异面直线的方法:
①定义法:由定义判断两直线不可能在同一平面内;
②排除法(反证法):排除两直线共面(平行或相交);
③重要结论(判定定理法):连接平面内一点与平面外一点的直线和这个平面内不经过此点的直线是异面直线.如图,A?α,B∈α,l?α,B?l?AB与l是异面直线.探究一探究二探究三思维辨析延伸探究在本例的正方体中,所有与直线AB异面的棱所在的直线为 .?
答案:CC1,B1C1,DD1,A1D1探究一探究二探究三思维辨析平行公理、等角定理的应用
例2如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠B1M1C1=∠BMC.
思路分析:(1)通过公理4证明MM1∥BB1,且MM1=BB1;(2)由(1)知B1M1∥BM,同理证得C1M1∥CM,再由等角定理证得∠BMC=∠B1M1C1.也可以通过证明△BCM≌△B1C1M1证出∠BMC=∠B1M1C1.探究一探究二探究三思维辨析证明:(1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,
∴MM1??AA1.
又AA1??BB1,
∴MM1∥BB1,且MM1=BB1,
∴四边形BB1M1M为平行四边形.探究一探究二探究三思维辨析(2)(方法一)由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
由(1)同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.∴∠BMC=∠B1M1C1.
(方法二)由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
由(1)同理可得四边形CC1M1M为平行四边形,
∴C1M1=CM.
又B1C1=BC,
∴△B1C1M1≌△BCM,
∴∠B1M1C1=∠BMC.探究一探究二探究三思维辨析反思感悟公理4及等角定理的应用
判断两直线平行仍是立体几何中的一个重要组成部分,除了平面几何中常用的判断方法以外,公理4也是判断两直线平行的重要依据.
证明角相等,利用空间等角定理是常用的思考方法;另外也可以通过证明两个三角形全等或相似来证明两角相等.在应用等角定理时,应注意当两个角的两边分别对应平行且方向都相同或相反时,这两个角相等,否则这两个角互补.因此,在证明两个角相等时,只说明两个角的两边分别对应平行是不够的.探究一探究二探究三思维辨析变式训练 已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:
(1)四边形MNA1C1是梯形;(2)∠DNM=∠D1A1C1.
证明(1)如图,连接AC,
在△ACD中,∵M,N分别是CD,AD的中点,
∴MN是△ACD的中位线,∴MN∥AC,MN= AC.
由正方体的性质,得AC∥A1C1,AC=A1C1.
∴MN∥A1C1,且MN= A1C1,即MN≠A1C1,∴四边形MNA1C1是梯形.
(2)由(1)可知MN∥A1C1,又∵ND∥A1D1,
∴∠DNM与∠D1A1C1相等或互补.
而∠DNM与∠D1A1C1均是直角三角形的一个锐角,
∴∠DNM=∠D1A1C1.探究一探究二探究三思维辨析求异面直线所成的角
例3 如图,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小.
思路分析:先作出角,再证明角的两边分别与两异面直线平行,最后在三角形中求角.探究一探究二探究三思维辨析解法一如图(1),连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,则OG∥B1D,EF∥A1C1.
∴∠GOA1为异面直线DB1与EF所成的角或其补角.
∵GA1=GC1,O为A1C1的中点,
∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.探究一探究二探究三思维辨析解法二如图(2),连接A1D,取A1D的中点H,连接HE,则HE∥DB1,且HE= DB1.
于是∠HEF为异面直线DB1与EF所成的角或补角.取A1D1的中点I,连接IF,IH,则HI⊥IF,
∴HF2=HI2+IF2= ,
∴HF2=EF2+HE2,∴∠HEF=90°,
∴异面直线DB1与EF所成的角为90°.探究一探究二探究三思维辨析解法三如图(3),在原正方体的右侧补上一个全等的正方体,连接B1Q,则B1Q∥EF.
于是∠DB1Q为异面直线DB1与EF所成的角或其补角.
通过计算,不难得到:B1D2+B1Q2=DQ2,从而异面直线DB1与EF所成的角为90°.探究一探究二探究三思维辨析反思感悟(1)求两条异面直线所成角的一般步骤
①构造:恰当地选择一个点(线段的端点或中点),用平移法构造异面直线所成的角;
②证明:证明①中所作出的角就是所求异面直线所成的角或其补角;
③计算:通过解三角形等知识,求出①中所构造的角的大小;
④结论:假如所构造的角的大小为α,若0°<α≤90°,则α即为所求异面直线所成角的大小;若90°<α<180°,则180°-α即为所求.
(2)作异面直线所成角的常用方法
①直接平移法(可利用图中已有的平行线);
②中位线平移法;
③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).探究一探究二探究三思维辨析(2)作出异面直线所成的角,可通过多种方法平移产生,主要有三种方法:
①直接平移法(可利用图中已有的平行线);
②中位线平移法;
③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).探究一探究二探究三思维辨析延伸探究若把“直线DB1”换为“直线DC1”呢?
解:如图,连接A1C1,A1D.
在△A1B1C1中,A1E=EB1,C1F=FB1,所以EF∥A1C1.所以∠A1C1D为直线DC1与EF所成的角.
在△A1C1D中,A1D=DC1=A1C1,
所以∠A1C1D=60°,
所以直线DC1与EF所成的角等于60°.探究一探究二探究三思维辨析一题多解——判断两条直线异面
典例如图,空间四边形ABCD,AB≠AC,AE是△ABC的BC边上的高,DF是△BCD的BC边上的中线,求证:AE和DF是异面直线.
点拨:根据题意画出示意图,由题设条件可知点E,F不重合,需结合AE和DF的位置关系判断.探究一探究二探究三思维辨析证法一(定理法)
由题设条件可知点E、F不重合,设△BCD所在平面为α.
证法二(反证法)
若AE和DF不是异面直线,则AE和DF共面,设过AE、DF的平面为β.
(1)若E,F重合,则E是BC中点,AB=AC,这与题设AB≠AC相矛盾.
(2)若E,F不重合,
∵B∈EF,C∈EF,EF?β,∴BC?β.
∵A∈β,D∈β,
∴A、B、C、D四点共面,这与题设四边形ABCD是空间四边形相矛盾.
综上,AE和DF不是异面直线不成立.
故AE和DF是异面直线.探究一探究二探究三思维辨析方法总结 判断两条直线异面常用的方法:
(1)定义法,不同在任一平面内的两条直线;
(2)定理法,过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.
(3)推论法,一条直线上两点与另一条与它异面的直线上两点所连成的两条直线为异面直线.123451.空间两条直线a、b与直线l都成异面直线,则a、b的位置关系是( )
A.平行或相交 B.异面或平行
C.异面或相交 D.平行或异面或相交
解析:直线a、b与直线l都成异面直线,a与b之间并没有任何限制,所以a与b直线的位置关系所有情况都可能.
答案:D123452.直线a与直线b相交,直线c与直线b相交,则直线a与直线c的位置关系是( )
A.相交 B.平行
C.异面 D.以上都有可能
解析:如图所示,在长方体ABCD-A1B1C1D1中,AB与AA1相交,A1B1与AA1相交,AB∥A1B1;又AD与AA1相交,AB与AD相交;又A1D1与AA1相交,AB与A1D1异面.故选D.
答案:D123453.一个无盖的正方体盒子展开后的平面图如图所示,A,B,C是展开图上的三点,则在正方体盒子中,∠ABC的大小是( )
A.45°
B.30°
C.60°
D.90°
解析:将平面图形折叠,得立体图,如图所示,可得△ABC的各边均为正方形的面对角线长,所以△ABC为等边三角形,所以∠ABC的大小为60°.故选C.
答案:C123454.已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于 ( )
A.30° B.30°或150°
C.150° D.以上结论都不对
解析:∠ABC的两边与∠PQR的两边分别平行,但方向不能确定是否相同.∴∠PQR=30°或150°.
答案:B123455.如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.则四边形EFGH是 .?
解析:连接BD,因为EH是△ABD的中位线,∴EH∥FG,且EH=FG.
∴四边形EFGH是平行四边形.
答案:平行四边形
