3.3.3 三角形的内角和课件(17张PPT)
文档属性
| 名称 | 3.3.3 三角形的内角和课件(17张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-05 00:00:00 | ||
图片预览


文档简介
课件17张PPT。三角形的内角和平行四边形、梯形和三角形情境导入探究新知课堂练习课堂小结课后作业同学们以小组为单位量一量课本57页
表格中每个三角形三个角的度数,并
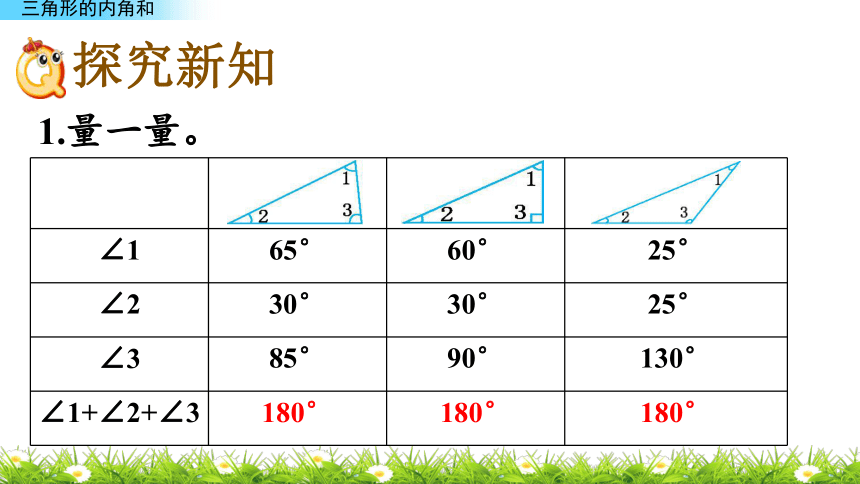
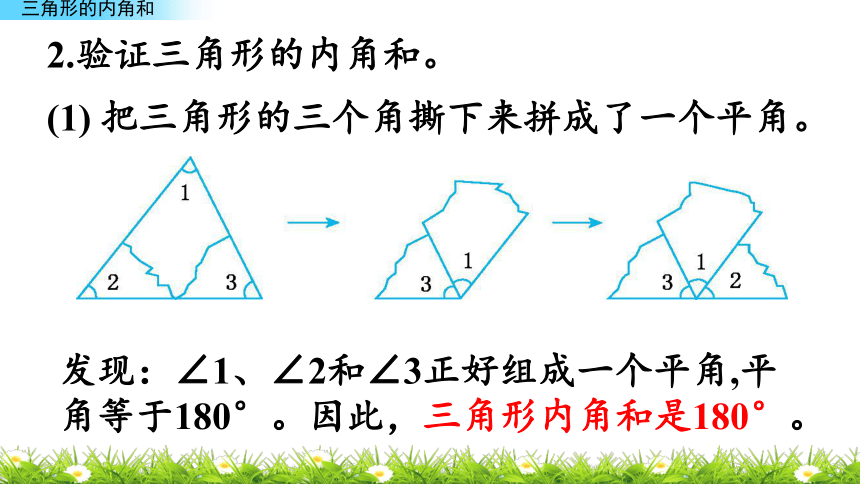
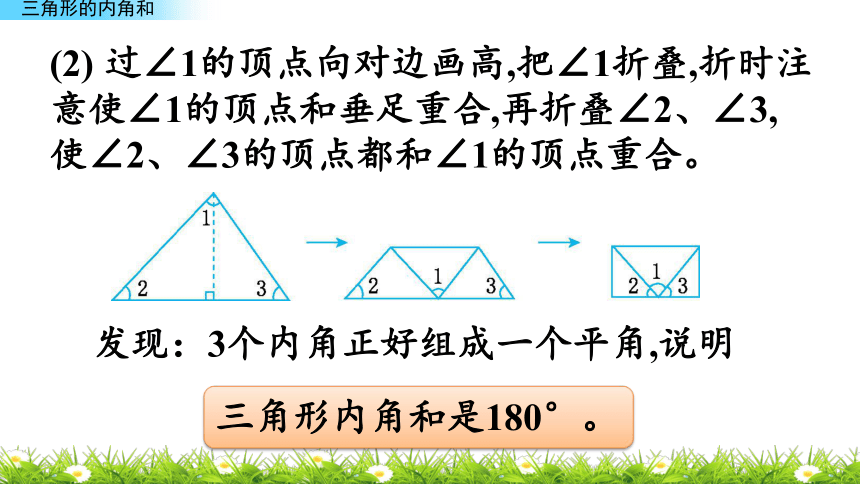
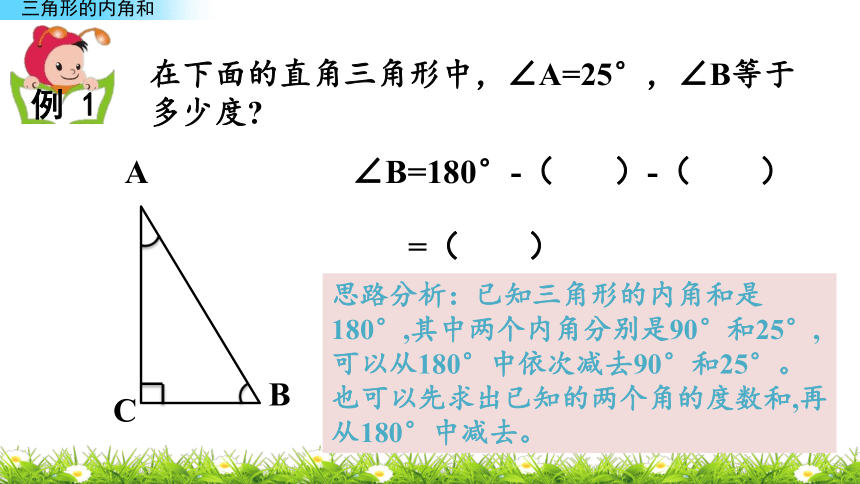
填入表格。一个正方形有4个内角,和是360°,把正方形纸对折成一个三角形,它有3个内角,和是180°。是不是所有的三角形内角和都是180°呢?1.量一量。如何来验证一下你的发现呢?观察你填入表格的数据,你发现了什么?我发现每个三角形三个角的和都是180°。2.验证三角形的内角和。(1) 把三角形的三个角撕下来拼成了一个平角。发现:∠1、∠2和∠3正好组成一个平角,平角等于180°。因此,三角形内角和是180°。(2) 过∠1的顶点向对边画高,把∠1折叠,折时注意使∠1的顶点和垂足重合,再折叠∠2、∠3,使∠2、∠3的顶点都和∠1的顶点重合。发现:3个内角正好组成一个平角,说明三角形内角和是180°。在下面的直角三角形中,∠A=25°,∠B等于多少度?例 1ABC∠B=180°-( )-( )=( )思路分析:已知三角形的内角和是180°,其中两个内角分别是90°和25°,可以从180°中依次减去90°和25°。也可以先求出已知的两个角的度数和,再从180°中减去。在下面的直角三角形中,∠A=25°,∠B等于多少度?例 1ABC∠B=180°-( )-( )=( )方法一:
∠B=180°-90°-25°=65°方法二:
∠B=180°-(90°+25°)=65°1.在三角形中,∠1=60°,∠2=45°。求∠3的度数。方法一:
∠3=180°-60°-45°=75°方法二:
∠3=180°-(60°+45°)=75°2.在三角形中,∠A=45°,∠B=115°,求∠C的度数?ABC方法一:
∠C=180°-45°-115°=20°方法二:
∠C=180°-(45°+115°)=20°3.把一个大三角形分成两个小三角形(如下图), 每个小三角形的和是多少度?三角形的内角和与它的形状、大小无关,所以每个小三角形的内角和依然是180°。4.一个等腰三角形的顶角是35°,它的一个底角是多少度?思路分析:等腰三角形的两个底角相等,所以已知等腰三角形的顶角度数,用180°减去顶角后除以2便可算出底角的度数。4.一个等腰三角形的顶角是35°,它的一个底角是多少度?(180°-35°)÷2=72.5°5.下面的说法对吗?为什么? (1)在三角形的内角中,最多只能有一个角是直角。 (1)对。因为如果三角形有两个或是更多角是直角,就不是三角形了,也超过三角形的内角和了。5.下面的说法对吗?为什么? (2)在三角形的内角中,至少有两个是锐角。 (2)对。因为如果只有一个角是锐角,那剩下的两个角就是直角或钝角,这样三角形的内角和就不是180°了。三角形的内角和是180°。
一个三角形中最多只有一个直角,至少有两个锐角。
这节课你有什么收获?你还有什么问题?
表格中每个三角形三个角的度数,并
填入表格。一个正方形有4个内角,和是360°,把正方形纸对折成一个三角形,它有3个内角,和是180°。是不是所有的三角形内角和都是180°呢?1.量一量。如何来验证一下你的发现呢?观察你填入表格的数据,你发现了什么?我发现每个三角形三个角的和都是180°。2.验证三角形的内角和。(1) 把三角形的三个角撕下来拼成了一个平角。发现:∠1、∠2和∠3正好组成一个平角,平角等于180°。因此,三角形内角和是180°。(2) 过∠1的顶点向对边画高,把∠1折叠,折时注意使∠1的顶点和垂足重合,再折叠∠2、∠3,使∠2、∠3的顶点都和∠1的顶点重合。发现:3个内角正好组成一个平角,说明三角形内角和是180°。在下面的直角三角形中,∠A=25°,∠B等于多少度?例 1ABC∠B=180°-( )-( )=( )思路分析:已知三角形的内角和是180°,其中两个内角分别是90°和25°,可以从180°中依次减去90°和25°。也可以先求出已知的两个角的度数和,再从180°中减去。在下面的直角三角形中,∠A=25°,∠B等于多少度?例 1ABC∠B=180°-( )-( )=( )方法一:
∠B=180°-90°-25°=65°方法二:
∠B=180°-(90°+25°)=65°1.在三角形中,∠1=60°,∠2=45°。求∠3的度数。方法一:
∠3=180°-60°-45°=75°方法二:
∠3=180°-(60°+45°)=75°2.在三角形中,∠A=45°,∠B=115°,求∠C的度数?ABC方法一:
∠C=180°-45°-115°=20°方法二:
∠C=180°-(45°+115°)=20°3.把一个大三角形分成两个小三角形(如下图), 每个小三角形的和是多少度?三角形的内角和与它的形状、大小无关,所以每个小三角形的内角和依然是180°。4.一个等腰三角形的顶角是35°,它的一个底角是多少度?思路分析:等腰三角形的两个底角相等,所以已知等腰三角形的顶角度数,用180°减去顶角后除以2便可算出底角的度数。4.一个等腰三角形的顶角是35°,它的一个底角是多少度?(180°-35°)÷2=72.5°5.下面的说法对吗?为什么? (1)在三角形的内角中,最多只能有一个角是直角。 (1)对。因为如果三角形有两个或是更多角是直角,就不是三角形了,也超过三角形的内角和了。5.下面的说法对吗?为什么? (2)在三角形的内角中,至少有两个是锐角。 (2)对。因为如果只有一个角是锐角,那剩下的两个角就是直角或钝角,这样三角形的内角和就不是180°了。三角形的内角和是180°。
一个三角形中最多只有一个直角,至少有两个锐角。
这节课你有什么收获?你还有什么问题?
