江苏省苏州市2008-2018学年高二(下)期末数学试卷(文科)分类汇编 :实际应用
文档属性
| 名称 | 江苏省苏州市2008-2018学年高二(下)期末数学试卷(文科)分类汇编 :实际应用 |  | |
| 格式 | zip | ||
| 文件大小 | 510.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-06 08:39:51 | ||
图片预览




文档简介
实际应用
(苏州市2008-2009高二 文(下)期末)17. 销售甲,乙两种商品所得利润分别为P(万元)和Q(万元),它们与投入资金t(万元)的关系有经验公式,。今将3万元资金投入经营甲,乙两种商品,其中对甲种商品投资万元
(1)试建立总利润(万元)关于的函数表达式
(2)求为多少时,总利润最大?并写出最大利润。
(苏州市2009-2010高二 文(下)期末)19.(本小题满分16分)光在某处的照度与光源的强度成正比,与光源距离的平方成反比.强度分别为8,1的两个光源A,B间的距离为6,在线段AB(除去端点)上有一点P,设PA=x.
(1)求x的值,使光源A与光源B在点P产生相等的照度;
(2)若“总照度”等于各照度之和.
①求出点P的“总照度”I(x)的表达式;②求最小“总照度”与相应的x值.
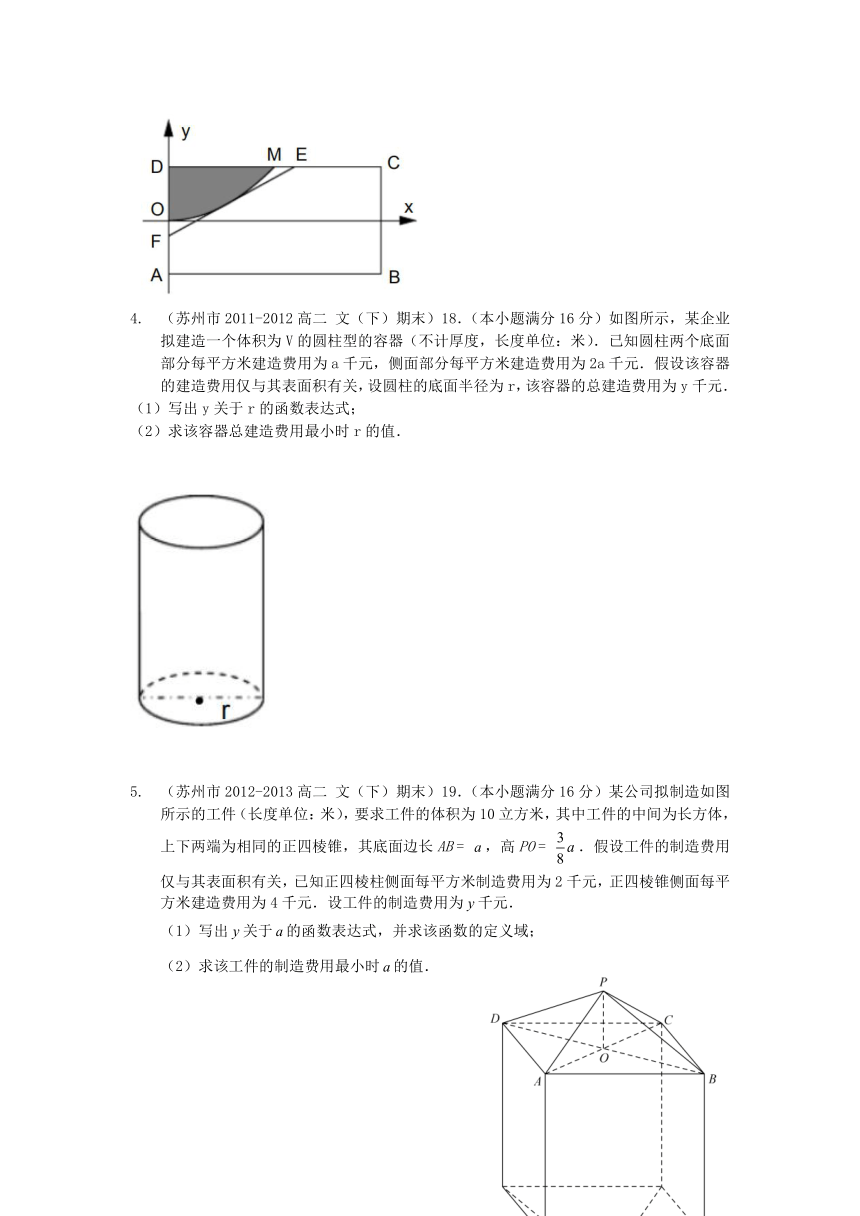
(苏州市2010-2011高二 文(下)期末)19.(本小题满分16分)有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分为一个五边形ABCEF,已知AB=4米,AD=2米.
如图所示建立直角坐标系,求边缘线OM的轨迹方程;
(2)①设点P(t,m)为边缘线OM上的一个动点,试求出点P处切线EF的方程(用t表示);
②求AF的值,使截去的△DEF的面积最小.
(苏州市2011-2012高二 文(下)期末)18.(本小题满分16分)如图所示,某企业拟建造一个体积为V的圆柱型的容器(不计厚度,长度单位:米).已知圆柱两个底面部分每平方米建造费用为a千元,侧面部分每平方米建造费用为2a千元.假设该容器的建造费用仅与其表面积有关,设圆柱的底面半径为r,该容器的总建造费用为y千元.
(1)写出y关于r的函数表达式;
(2)求该容器总建造费用最小时r的值.
(苏州市2012-2013高二 文(下)期末)19.(本小题满分16分)某公司拟制造如图所示的工件(长度单位:米),要求工件的体积为10立方米,其中工件的中间为长方体,上下两端为相同的正四棱锥,其底面边长AB = ,高PO = .假设工件的制造费用仅与其表面积有关,已知正四棱柱侧面每平方米制造费用为2千元,正四棱锥侧面每平方米建造费用为4千元.设工件的制造费用为千元.
(1)写出关于的函数表达式,并求该函数的定义域;
(
(第
19
题)
)(2)求该工件的制造费用最小时的值.
(苏州市2013-2014高二 文(下)期末)18.(本小题满分16分)某企业生产一种产品,日产量基本保持在万件到0万件之间,由于受技术水平等因素的影响,会产生一些次品,根据统计分析,其次品率()与日产量(万件)之间基本满足关系:目前,每生产万件合格的产品可以盈利万元,但每生产万件次品将亏损万元.
(1)试将生产这种产品每天的盈利额(万元)表示为日产量(万件)的函数;
(2)问当生产这种产品的日产量约为多少时(精确到万件),企业可获得最大
利润?
(苏州市2014-2015高二 文(下)期末)19.(本小题满分16分)某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年增加2万元,从第八年开始,每年的维护费用比上年增加25%.
(1)设第n年该生产线的维护费用为a????万元,求a????的表达式;
(2)若该生产线前n年每年的平均维护费用大于12万元时,需要更新生产线.试求该生产线前n年每年的平均维护费用,并判断第几年年初需要更新该生产线?
(苏州市2015-2016(2017-2018)高二 文(下)期末)18.(本小题满分16分)如图,某工厂根据生产需要制作一种下部是圆柱、上部是圆锥的封闭型组合体存储设备,该组合体总高度为8米,圆柱的底面半径为4米,圆柱的高不小于圆柱的底面半径.已知制作圆柱侧面和底面的造价均为每平米2百元,制作圆锥侧面的造价为每平米4百元,设制作该存储设备的总费用为y百元.
(1)按下列要求写出函数关系式:
①设(米),将y表示成h的函数关系式;
②设(rad),将y表示成θ的函数关系式;
(
第
18
题图
)(2)请你选用其中的一个函数关系式,求制作该存储设备总费用的最小值.
(苏州市2016-2017高二 文(下)期末)18.在一张边长为10分米的正三角形铁皮的3个角上,各剪去1个相同的四边形(如图所示),折成一个高为x分米的无盖正三棱柱容器(如图所示),其容积为y升(1升等于1立方分米)。
试写出用x表示y的函数关系式,并指出它的定义域;
求这个正三棱柱容器容积的最大值,并求此时这个正三棱柱的高。
答案:
(1)由题意知,点P受光源A的照度为,受光源B的照度为,其中k为比例常数;
∵光源A与光源B在点P产生相等的照度,
∴=,
由0<x<6,得x=2(6-x),
∴x=;
(2)①点P的“总照度”I(x)=+,(0<x<6),
②由I′(x)=-+,,且I'(x)=0,解得x=4.
所以,0<x<4时,I'(x)<0,I(x)在(0,4)上单调递减;
当4<x<6时,I(x)<0,I(x)在(4,6)上单调递增;
因此,=4时,I(x)取得最小值为
(1)如图,以O点为原点,OD所在直线为y轴,建立直角坐标系,
则D(0,1),直线AB方程为y=-1
∵OM上每一点到点D的距离都等于它到边AB的距离,
∴OM的轨迹为以D点为焦点,以AB为直径的抛物线的一部分,
∴OM的轨迹方程为x2=4y(0≤x≤2)
(2)①∵点P(t,m)在曲线x2=4y,∴t2=4m,m=
曲线x2=4y可化为y=,求导,得,y′=
∴曲线在点P处切线斜率k=,
切线EF的方程为y-m=(x-t)
把m=代入,得,y-=(x-t)
②令切线y-=(x-t)x=0,得y=-
令y=1,得,x=+
∴S△DEF=|DE||DF|=(1+)(+)=++
∴S′△DEF=+-,
当t∈[0,1]时,S′△DEF<0
∴S△DEF随t的增大而减小,
∵0≤t≤1,∴当t=1时,S△DEF有最小值为
此时F点坐标为(0,-),AF=
∴当AF=时,截去的△DEF的面积最小.
(4)18.解:(1)设圆柱的高为h,
∵,∴.………………2分
∴r>0).………………6分
(2).………………8分
令,得.………………10分
(0,) (,+∞)
- 0 +
y ↘ 极小值 ↗
∴该容器总建造费用最小时.…………………16分
(5)19.解:(1)AB = ,PO = ,∴斜高为.………… 2分
∴一个正四棱锥的侧面积为.
一个正四棱锥的体积为. …………… 4分
令长方体的高为,则.∴. …………… 6分
由,得. …………… 8分
,定义域为.……… 11分
(2),令,得. …………… 13分
当,,y为a的减函数;
当,,y为a的增函数, …………… 15分
(答)该工件的制造费用最小时,的值为(米). …………… 16分
(6)18.(1) …………… 2分
…………… 6分
(2)当时,; …………… 8分
当时,∵,令,得(舍去).
…………… 12分
∵在(5,10]上图象不间断,
∴在(5,10]上最大值. …………… 13分
∵,在[1,10]上最大值在时取得. …………… 15分
答:当生产这种产品的日产量为万件时,企业可获得最大利润.……… 16分
(7)
(8)
18.解:(1)① S圆柱侧2?rh8?h,S圆锥侧?rl,……………………2分
(注:定义域不写扣1分)
y2S底面+ 2S圆柱侧+4 S圆锥侧=32?+16?h+
= 32?+,(); ………………………4分
② ,.
y2S底面+ 2S圆柱侧4 S圆锥侧=32?++
32?++=160?+64?().………………………8分
(2)选方案①
由(1)知32?+,().
设,则y 32?+=32?+,………11分
32?+在上单调递减, ………………………13分
所以,当时,y取到最小值. ………………………15分
选方案②
由(1)知y=160?+64?.(),
设,, ………………………10分
因为,,所以,,
所以,在上单调递减, ………………………13分
所以,当时,y取到最小值. ………………………15分
答:制作该存储设备总费用的最小值为百元. ……………………16分
(9)(Ⅰ)因为容器的高为?x?,则做成的正三棱柱形容器的底边长为10-2x?.
则y=(10-2x)2x??? .?
函数的定义域为(0,)?.???
(Ⅱ)实际问题归结为求函数?y在区间(0,)?上的最大值点.先求?y的极值点.在开区间?(0,)内,y‘=9x2-60x+25’
令?y‘=0,即令9x2-60x+25=0?,解得x1=,x2=?.
(∞,) (,) (,∞)
+ 0 0
↗ 极大值 ↘ 极小值 ↗
所以x=?是y?的最大值点,并且最大值f()=???
即当正三棱柱形容器高为?时,容器的容积最大为
(
1
) (
第页共
1
页
)
(苏州市2008-2009高二 文(下)期末)17. 销售甲,乙两种商品所得利润分别为P(万元)和Q(万元),它们与投入资金t(万元)的关系有经验公式,。今将3万元资金投入经营甲,乙两种商品,其中对甲种商品投资万元
(1)试建立总利润(万元)关于的函数表达式
(2)求为多少时,总利润最大?并写出最大利润。
(苏州市2009-2010高二 文(下)期末)19.(本小题满分16分)光在某处的照度与光源的强度成正比,与光源距离的平方成反比.强度分别为8,1的两个光源A,B间的距离为6,在线段AB(除去端点)上有一点P,设PA=x.
(1)求x的值,使光源A与光源B在点P产生相等的照度;
(2)若“总照度”等于各照度之和.
①求出点P的“总照度”I(x)的表达式;②求最小“总照度”与相应的x值.
(苏州市2010-2011高二 文(下)期末)19.(本小题满分16分)有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分为一个五边形ABCEF,已知AB=4米,AD=2米.
如图所示建立直角坐标系,求边缘线OM的轨迹方程;
(2)①设点P(t,m)为边缘线OM上的一个动点,试求出点P处切线EF的方程(用t表示);
②求AF的值,使截去的△DEF的面积最小.
(苏州市2011-2012高二 文(下)期末)18.(本小题满分16分)如图所示,某企业拟建造一个体积为V的圆柱型的容器(不计厚度,长度单位:米).已知圆柱两个底面部分每平方米建造费用为a千元,侧面部分每平方米建造费用为2a千元.假设该容器的建造费用仅与其表面积有关,设圆柱的底面半径为r,该容器的总建造费用为y千元.
(1)写出y关于r的函数表达式;
(2)求该容器总建造费用最小时r的值.
(苏州市2012-2013高二 文(下)期末)19.(本小题满分16分)某公司拟制造如图所示的工件(长度单位:米),要求工件的体积为10立方米,其中工件的中间为长方体,上下两端为相同的正四棱锥,其底面边长AB = ,高PO = .假设工件的制造费用仅与其表面积有关,已知正四棱柱侧面每平方米制造费用为2千元,正四棱锥侧面每平方米建造费用为4千元.设工件的制造费用为千元.
(1)写出关于的函数表达式,并求该函数的定义域;
(
(第
19
题)
)(2)求该工件的制造费用最小时的值.
(苏州市2013-2014高二 文(下)期末)18.(本小题满分16分)某企业生产一种产品,日产量基本保持在万件到0万件之间,由于受技术水平等因素的影响,会产生一些次品,根据统计分析,其次品率()与日产量(万件)之间基本满足关系:目前,每生产万件合格的产品可以盈利万元,但每生产万件次品将亏损万元.
(1)试将生产这种产品每天的盈利额(万元)表示为日产量(万件)的函数;
(2)问当生产这种产品的日产量约为多少时(精确到万件),企业可获得最大
利润?
(苏州市2014-2015高二 文(下)期末)19.(本小题满分16分)某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年增加2万元,从第八年开始,每年的维护费用比上年增加25%.
(1)设第n年该生产线的维护费用为a????万元,求a????的表达式;
(2)若该生产线前n年每年的平均维护费用大于12万元时,需要更新生产线.试求该生产线前n年每年的平均维护费用,并判断第几年年初需要更新该生产线?
(苏州市2015-2016(2017-2018)高二 文(下)期末)18.(本小题满分16分)如图,某工厂根据生产需要制作一种下部是圆柱、上部是圆锥的封闭型组合体存储设备,该组合体总高度为8米,圆柱的底面半径为4米,圆柱的高不小于圆柱的底面半径.已知制作圆柱侧面和底面的造价均为每平米2百元,制作圆锥侧面的造价为每平米4百元,设制作该存储设备的总费用为y百元.
(1)按下列要求写出函数关系式:
①设(米),将y表示成h的函数关系式;
②设(rad),将y表示成θ的函数关系式;
(
第
18
题图
)(2)请你选用其中的一个函数关系式,求制作该存储设备总费用的最小值.
(苏州市2016-2017高二 文(下)期末)18.在一张边长为10分米的正三角形铁皮的3个角上,各剪去1个相同的四边形(如图所示),折成一个高为x分米的无盖正三棱柱容器(如图所示),其容积为y升(1升等于1立方分米)。
试写出用x表示y的函数关系式,并指出它的定义域;
求这个正三棱柱容器容积的最大值,并求此时这个正三棱柱的高。
答案:
(1)由题意知,点P受光源A的照度为,受光源B的照度为,其中k为比例常数;
∵光源A与光源B在点P产生相等的照度,
∴=,
由0<x<6,得x=2(6-x),
∴x=;
(2)①点P的“总照度”I(x)=+,(0<x<6),
②由I′(x)=-+,,且I'(x)=0,解得x=4.
所以,0<x<4时,I'(x)<0,I(x)在(0,4)上单调递减;
当4<x<6时,I(x)<0,I(x)在(4,6)上单调递增;
因此,=4时,I(x)取得最小值为
(1)如图,以O点为原点,OD所在直线为y轴,建立直角坐标系,
则D(0,1),直线AB方程为y=-1
∵OM上每一点到点D的距离都等于它到边AB的距离,
∴OM的轨迹为以D点为焦点,以AB为直径的抛物线的一部分,
∴OM的轨迹方程为x2=4y(0≤x≤2)
(2)①∵点P(t,m)在曲线x2=4y,∴t2=4m,m=
曲线x2=4y可化为y=,求导,得,y′=
∴曲线在点P处切线斜率k=,
切线EF的方程为y-m=(x-t)
把m=代入,得,y-=(x-t)
②令切线y-=(x-t)x=0,得y=-
令y=1,得,x=+
∴S△DEF=|DE||DF|=(1+)(+)=++
∴S′△DEF=+-,
当t∈[0,1]时,S′△DEF<0
∴S△DEF随t的增大而减小,
∵0≤t≤1,∴当t=1时,S△DEF有最小值为
此时F点坐标为(0,-),AF=
∴当AF=时,截去的△DEF的面积最小.
(4)18.解:(1)设圆柱的高为h,
∵,∴.………………2分
∴r>0).………………6分
(2).………………8分
令,得.………………10分
(0,) (,+∞)
- 0 +
y ↘ 极小值 ↗
∴该容器总建造费用最小时.…………………16分
(5)19.解:(1)AB = ,PO = ,∴斜高为.………… 2分
∴一个正四棱锥的侧面积为.
一个正四棱锥的体积为. …………… 4分
令长方体的高为,则.∴. …………… 6分
由,得. …………… 8分
,定义域为.……… 11分
(2),令,得. …………… 13分
当,,y为a的减函数;
当,,y为a的增函数, …………… 15分
(答)该工件的制造费用最小时,的值为(米). …………… 16分
(6)18.(1) …………… 2分
…………… 6分
(2)当时,; …………… 8分
当时,∵,令,得(舍去).
…………… 12分
∵在(5,10]上图象不间断,
∴在(5,10]上最大值. …………… 13分
∵,在[1,10]上最大值在时取得. …………… 15分
答:当生产这种产品的日产量为万件时,企业可获得最大利润.……… 16分
(7)
(8)
18.解:(1)① S圆柱侧2?rh8?h,S圆锥侧?rl,……………………2分
(注:定义域不写扣1分)
y2S底面+ 2S圆柱侧+4 S圆锥侧=32?+16?h+
= 32?+,(); ………………………4分
② ,.
y2S底面+ 2S圆柱侧4 S圆锥侧=32?++
32?++=160?+64?().………………………8分
(2)选方案①
由(1)知32?+,().
设,则y 32?+=32?+,………11分
32?+在上单调递减, ………………………13分
所以,当时,y取到最小值. ………………………15分
选方案②
由(1)知y=160?+64?.(),
设,, ………………………10分
因为,,所以,,
所以,在上单调递减, ………………………13分
所以,当时,y取到最小值. ………………………15分
答:制作该存储设备总费用的最小值为百元. ……………………16分
(9)(Ⅰ)因为容器的高为?x?,则做成的正三棱柱形容器的底边长为10-2x?.
则y=(10-2x)2x??? .?
函数的定义域为(0,)?.???
(Ⅱ)实际问题归结为求函数?y在区间(0,)?上的最大值点.先求?y的极值点.在开区间?(0,)内,y‘=9x2-60x+25’
令?y‘=0,即令9x2-60x+25=0?,解得x1=,x2=?.
(∞,) (,) (,∞)
+ 0 0
↗ 极大值 ↘ 极小值 ↗
所以x=?是y?的最大值点,并且最大值f()=???
即当正三棱柱形容器高为?时,容器的容积最大为
(
1
) (
第页共
1
页
)
