江苏省苏州市2008-2018学年高二(下)期末数学试卷(文科)分类汇编:解析几何
文档属性
| 名称 | 江苏省苏州市2008-2018学年高二(下)期末数学试卷(文科)分类汇编:解析几何 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-06 08:41:07 | ||
图片预览




文档简介
直线与圆的方程
(苏州市2008-2009高二 文(下)期末)8.直线相交于两点,则
(苏州市2009-2010高二 文(下)期末)11.直线x+2y-3=0被圆(x-2)2+(y+1)2=4截得的弦长为 .
(苏州市2010-2011高二 文(下)期末)10.已知圆x2+y2=m与圆x2+y2+6x-8y-11=0相交,则实数m的取值范围为 。
(苏州市2011-2012高二 文(下)期末)12.若圆上存在两个点P,Q,它们到直线y=kx+1的距离都等于1,则实数k的取值范围为 .
(苏州市2012-2013高二 文(下)期末)12.设P是直线上的一个动点,过P作圆的两条切线,若的最大值为60,则b = .
(苏州市2013-2014高二 文(下)期末)11.在平面直角坐标系xOy中,设直线与圆相交于A,B两点,则线段AB的长为 .
(苏州市2014-2015高二 文(下)期末)10.在平面直角坐标系????????????中,若圆????的半径为1,圆心在第一象限,且与直线4?????3????=0和????轴都相切, 则该圆的标准方程为 .
(苏州市2015-2016(2017-2018)高二 文(下)期末)9.若圆C过两点,且圆心C在直线x-2y-2=0上,则圆C的标准方程为 .
(苏州市2016-2017高二 文(下)期末)5.在平面直角坐标系xOy中,已知点P(x,y)在直线x+y-4=0上,则OP的最小值为 .
(苏州市2016-2017高二 文(下)期末)12.在平面直角坐标系xOy中,已知圆C:x2+(y-1)2=4,若等边三角形ΔPAB的一边AB为圆C的一条弦,则PC的最大值为 .
圆锥曲线
(苏州市2008-2009高二 文(下)期末)14.已知抛物线的焦点F也是双曲线的一个焦点,过F作直线与轴垂直,与交于两点,与交于两点,则
(苏州市2008-2009高二 文(下)期末)19. 已知椭圆的短轴长为4,分别是椭圆的左,右焦点,直线与椭圆在第一象限内的交点为,的面积为,点是椭圆上的动点
求椭圆的方程
若为钝角,求点的横坐标的取值范围
(苏州市2009-2010高二 文(下)期末)2.抛物线y2=4x的焦点坐标为
(苏州市2009-2010高二 文(下)期末)5?.双曲线的离心率为 ?
(苏州市2009-2010高二 文(下)期末)13.已知点M是椭圆(a>b>0)上的一点,过M作斜率分别为k1,k2的直线,交椭圆于A,B两点,且A,B关于原点对称,则k1k2=-.类比椭圆的这个性质,设M是双曲线(a>0,b>0上的一点,过M作斜率分别为k1,k2的直线,交双曲线于A,B两点,且A,B关于原点对称,则k1k2= 。
(苏州市2009-2010高二 文(下)期末)16.(本小题满分14分)在平面直角坐标系xOy中,椭圆C:的离心率为,且椭圆C过点A(2,).
(1)求椭圆C的方程;
(2)设点B为椭圆C的下顶点,直线y=-x与椭圆相交于P,Q,求ΔBPQ的面积S.
(苏州市2010-2011高二 文(下)期末)4.双曲线的右焦点到右准线距离为?
(苏州市2010-2011高二 文(下)期末)12.已知A,B,F分别是椭圆(a>b>0)的上、下顶点和右焦点,直线AF与椭圆右准线交于点MB∥x轴,则该椭圆的离心率e=
(苏州市2010-2011高二 文(下)期末)17.(本小题满分14分)在直角坐标平面xoy中,椭圆E:+y2=1的左顶点为A,下顶点为B。
(1)求圆心在y轴上且过两点A,B的圆方程;
(苏州市2011-2012高二 文(下)期末)5.抛物线x2=4y上的点P到焦点的距离是4,则点P的纵坐标为 .
(苏州市2011-2012高二 文(下)期末)14.如图,在平面直角坐标系xOy中,已知椭圆E:的右焦点为F,点A,B在椭圆E上,直线AB经过坐标原点O.若AF⊥x轴,,则椭圆E的离心率e= .
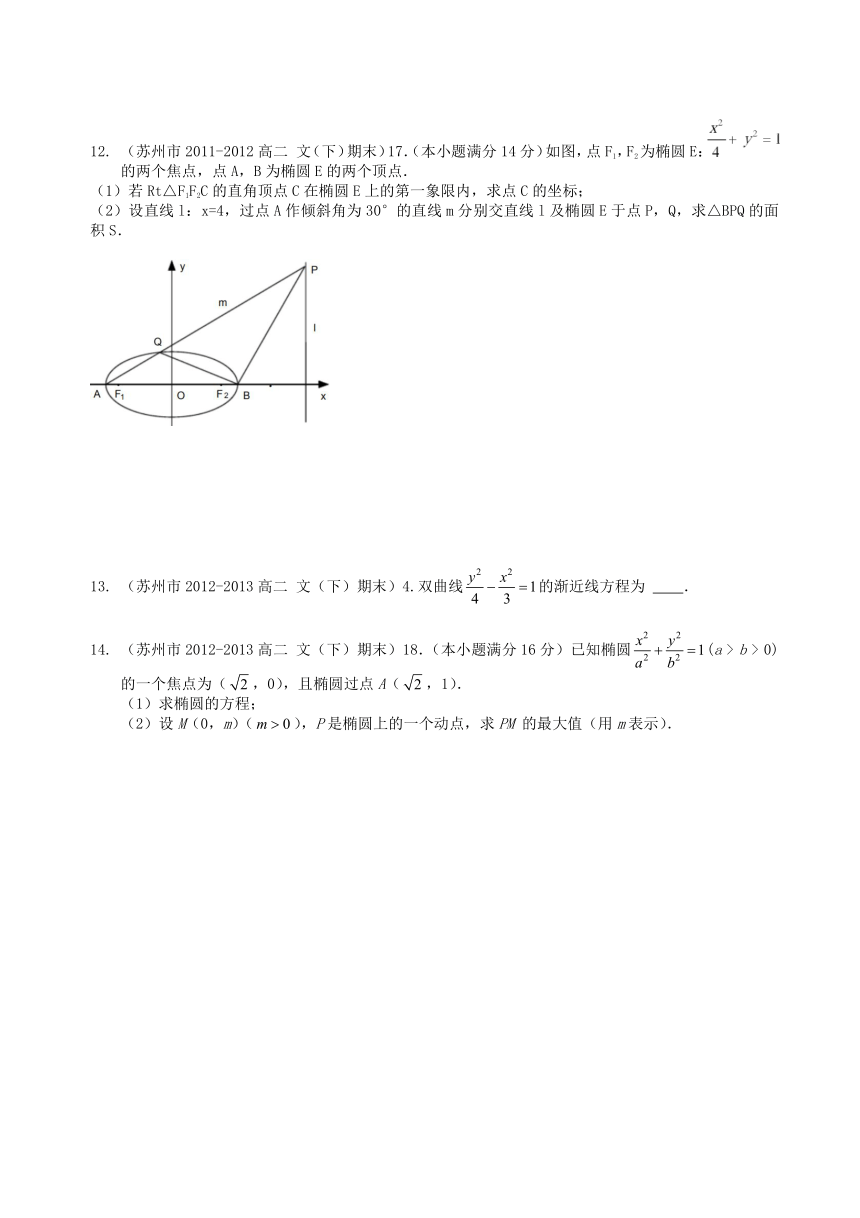
(苏州市2011-2012高二 文(下)期末)17.(本小题满分14分)如图,点F1,F2为椭圆E:的两个焦点,点A,B为椭圆E的两个顶点.
(1)若Rt△F1F2C的直角顶点C在椭圆E上的第一象限内,求点C的坐标;
(2)设直线l:x=4,过点A作倾斜角为30°的直线m分别交直线l及椭圆E于点P,Q,求△BPQ的面积S.
(苏州市2012-2013高二 文(下)期末)4.双曲线的渐近线方程为 .
(苏州市2012-2013高二 文(下)期末)18.(本小题满分16分)已知椭圆(a > b > 0)的一个焦点为(,0),且椭圆过点A(,1).
(1)求椭圆的方程;
(2)设M(0,m)(),P是椭圆上的一个动点,求PM 的最大值(用m表示).
(苏州市2013-2014高二 文(下)期末)3.抛物线的准线方程为 .
(苏州市2013-2014高二 文(下)期末)17.(本小题满分14分)如图,在平面直角坐标系xOy中,椭圆的左、右顶点分别为A,B,左、右焦点分别为F1,F2,点在椭圆上,且直线的斜率之积为.
(1)求椭圆的离心率;
(
F
F
x
y
A
B
1
2
M
O
)(2)若点又在以线段F1F2为直径的圆上,且△MAB的面积为, 求椭圆的方程.
(苏州市2014-2015高二 文(下)期末)3.双曲线-=1的离心率为 .
(苏州市2014-2015高二 文(下)期末)18.(本小题满分 16 分)平面直角坐标系 ???????????? 中,已知圆心在第二象限,半径为 2的圆 ???? 与直线????=????相切于坐标原点O,椭圆+=1(????>0)与圆????的一个交点到椭圆的两焦点的距离之和为10.
(1)求圆????的方程;
(2)若圆????上存在一点????(异于坐标原点),满足点????到椭圆右焦点????的距离等于????????的长,试求出点????的坐标.
(苏州市2015-2016(2017-2018)高二 文(下)期末)3.双曲线的离心率为2,则a= .
(苏州市2015-2016(2017-2018)高二 文(下)期末)11.已知过点A(-3,-2)的直线与抛物线C:x2=8y在第二象限相切于点B,记抛物线C的焦点为F,则直线BF的斜率为 .
(苏州市2015-2016(2017-2018)高二 文(下)期末)14.若实数a,b满足,则a的最大值是 .
(苏州市2015-2016(2017-2018)高二 文(下)期末)19.(本小题满分16分)如图,已知椭圆M:的离心率为,且过点.
(1)求椭圆M的标准方程;
(2)设点是椭圆M上异于顶点的任意两点,直线OA,OB的斜率分别为,且.
①求的值;
(
第
19
题图
A
B
C
O
) ②设点B关于x轴的对称点为C,试求直线 AC的斜率.
(苏州市2016-2017高二 文(下)期末)3.在平面直角坐标系xOy中,双曲线-=1的离心率为 .
(苏州市2016-2017高二 文(下)期末)10.在平面直角坐标系xOy中,过抛物线y2=4x的焦点F作弦AB,则●= . (
5
) (
第页共
1
页
)
(苏州市2016-2017高二 文(下)期末)19.在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0),其焦点到相应准线的距离为,离心率为.
(1)求椭圆C的标准方程; (
6
) (
第页共
3
页
)
(2)如图所示A,B是椭圆C上两点,且△AOB的面积为,设射线OA,OB的斜率分别为k1,k2
①求k1●k2的值.
②延长OA到P,使得OP=2OA,且PB交椭圆C于Q,求证为定值.
答案:
直线与圆的方程
4
1<m<121
(x-2)2+(y-1)2=1
5
4
圆锥曲线
7
【答案】
(1)∵2b=4,∴b=2,①
由题意,设A(x,x)(x>0),则,②
AF1F2的面积为2,∴cx=2③,
由①②③得:a=2,椭圆C的方程为:.
(2)设p(x,y),则 F1(-2,0),F2(2,0),
且∠F1PF2是钝角
?PF12+PF22<F1F22?(x+2)2+y2+(x-2)2+y2<32
?x2+y2<8?-<x<.
(1,0)
解(1)因为椭圆的离心率为 ,
所以 a=2c.
又因为椭圆C过点A(2, ),
所以.
由以上结合a2=b2+c2可得:a2=16,b2=4.
所以椭圆的方程为: .
(2)设P(x1,y1),Q(x2,y2)
联立直线与椭圆的方程:
,解得P( ,- ),Q(- , ),
因为点B为椭圆C的下顶点,
所以△BPQ的面积S= ×b×|x1-x2|=
所以△BPQ的面积S为
(1)∵椭圆E:+y2=1的
a=2,b=1,c=,
∴左顶点为A(-2,0),下顶点为B(0,-1).
线段AB的垂直平分线的方程为:y-(-)=2(x+1)
令x=0得它与y轴的交点坐标为(0,),
即圆心在y轴上且过两点A,B的圆的圆心坐标为(0,),
故其半径r=1+=,
∴圆心在y轴上且过两点A,B的圆方程:x2+(y-)2=;
(2)∵△OAP与△OCP的面积相等,
∴P是线段AC的中点,
设C(0,2n),则P(-1,n)代入椭圆的方程得:
+n?2=1,又点A作直线l交椭圆于点P,交y正半轴于点C,故n=,
∴C(0,),又A(-2,0),
直线l的斜率k==
3
17.解:(1)椭圆E中,a2=4,b2=1,c2=3,
F1(-,0),F2(,0),…………………2分
A(-2,0),B(2,0),设C(x,y).
∵∠F1CF290°,∴OC=OF2=.则x2+y2=3.…………………4分
又,∴x2=,y2=.
∵点C在第一象限内,x>0,y>0,
∴,.即C(,).…………………7分
(2)直线AQ方程为:.
与椭圆E方程联立得
, …………………9分
即.∴xQ=.则Q.…………………11分
又, …………………12分
∴△BPQ的面积S=S△ABP-S△ABQ=.…………14分
18.解:(1)由题意,c =,则. ………… 2分
可设椭圆方程为.
∵椭圆过点(,1),∴,解得. ……… 4分
(或由椭圆定义,得,则a = 2,同样得2分)
∴椭圆方程为. ……………… 6分
(2)设,则.
∴. …………… 9分
由,得. …………… 11分
∴当时,在y0 = m时,得PM的最大值为; …………13分
当时,在y0 = 时,得PM的最大值为. ………… 15分
即 ………… 16分
(1),设,则.
, …………… 4分
∵的斜率之积为,.
∵a2 = b2 c2,.
,故椭圆的离心率. …………… 6分
(2)设,则.
由(1)知,,即.① ………… 8分
∵点又在以线段F1F2为直径的圆上,,
而,∴.② ………… 10分
又∵,.③ …………… 12分
由①,②,③,解得.
故椭圆的标准方程为. …………… 14分
1
-
20
19.解(1)由题意,所以,即,
所以椭圆M的方程为, ………………………2分
又因为椭圆M过点,所以,即.
所以所求椭圆M的标准方程为. ………………………4分
(2)①设直线OA的方程为,
化简得,解得, ………………………6分
因为,故,
同理可得, ………………………8分
所以. ………………………10分
②由题意,点B关于x轴的对称点为C的坐标为,
又点是椭圆M上异于顶点的任意两点,
所以,故,即.
………………………12分
设直线AC的斜率为k,则,
因为,即,故,
所以, ………………………15分
所以直线AC的斜率为k为常数,即或. ………………………16分
-3
(
12
) (
第页共
3
页
)
(
13
) (
第页共
1
页
)
(苏州市2008-2009高二 文(下)期末)8.直线相交于两点,则
(苏州市2009-2010高二 文(下)期末)11.直线x+2y-3=0被圆(x-2)2+(y+1)2=4截得的弦长为 .
(苏州市2010-2011高二 文(下)期末)10.已知圆x2+y2=m与圆x2+y2+6x-8y-11=0相交,则实数m的取值范围为 。
(苏州市2011-2012高二 文(下)期末)12.若圆上存在两个点P,Q,它们到直线y=kx+1的距离都等于1,则实数k的取值范围为 .
(苏州市2012-2013高二 文(下)期末)12.设P是直线上的一个动点,过P作圆的两条切线,若的最大值为60,则b = .
(苏州市2013-2014高二 文(下)期末)11.在平面直角坐标系xOy中,设直线与圆相交于A,B两点,则线段AB的长为 .
(苏州市2014-2015高二 文(下)期末)10.在平面直角坐标系????????????中,若圆????的半径为1,圆心在第一象限,且与直线4?????3????=0和????轴都相切, 则该圆的标准方程为 .
(苏州市2015-2016(2017-2018)高二 文(下)期末)9.若圆C过两点,且圆心C在直线x-2y-2=0上,则圆C的标准方程为 .
(苏州市2016-2017高二 文(下)期末)5.在平面直角坐标系xOy中,已知点P(x,y)在直线x+y-4=0上,则OP的最小值为 .
(苏州市2016-2017高二 文(下)期末)12.在平面直角坐标系xOy中,已知圆C:x2+(y-1)2=4,若等边三角形ΔPAB的一边AB为圆C的一条弦,则PC的最大值为 .
圆锥曲线
(苏州市2008-2009高二 文(下)期末)14.已知抛物线的焦点F也是双曲线的一个焦点,过F作直线与轴垂直,与交于两点,与交于两点,则
(苏州市2008-2009高二 文(下)期末)19. 已知椭圆的短轴长为4,分别是椭圆的左,右焦点,直线与椭圆在第一象限内的交点为,的面积为,点是椭圆上的动点
求椭圆的方程
若为钝角,求点的横坐标的取值范围
(苏州市2009-2010高二 文(下)期末)2.抛物线y2=4x的焦点坐标为
(苏州市2009-2010高二 文(下)期末)5?.双曲线的离心率为 ?
(苏州市2009-2010高二 文(下)期末)13.已知点M是椭圆(a>b>0)上的一点,过M作斜率分别为k1,k2的直线,交椭圆于A,B两点,且A,B关于原点对称,则k1k2=-.类比椭圆的这个性质,设M是双曲线(a>0,b>0上的一点,过M作斜率分别为k1,k2的直线,交双曲线于A,B两点,且A,B关于原点对称,则k1k2= 。
(苏州市2009-2010高二 文(下)期末)16.(本小题满分14分)在平面直角坐标系xOy中,椭圆C:的离心率为,且椭圆C过点A(2,).
(1)求椭圆C的方程;
(2)设点B为椭圆C的下顶点,直线y=-x与椭圆相交于P,Q,求ΔBPQ的面积S.
(苏州市2010-2011高二 文(下)期末)4.双曲线的右焦点到右准线距离为?
(苏州市2010-2011高二 文(下)期末)12.已知A,B,F分别是椭圆(a>b>0)的上、下顶点和右焦点,直线AF与椭圆右准线交于点MB∥x轴,则该椭圆的离心率e=
(苏州市2010-2011高二 文(下)期末)17.(本小题满分14分)在直角坐标平面xoy中,椭圆E:+y2=1的左顶点为A,下顶点为B。
(1)求圆心在y轴上且过两点A,B的圆方程;
(苏州市2011-2012高二 文(下)期末)5.抛物线x2=4y上的点P到焦点的距离是4,则点P的纵坐标为 .
(苏州市2011-2012高二 文(下)期末)14.如图,在平面直角坐标系xOy中,已知椭圆E:的右焦点为F,点A,B在椭圆E上,直线AB经过坐标原点O.若AF⊥x轴,,则椭圆E的离心率e= .
(苏州市2011-2012高二 文(下)期末)17.(本小题满分14分)如图,点F1,F2为椭圆E:的两个焦点,点A,B为椭圆E的两个顶点.
(1)若Rt△F1F2C的直角顶点C在椭圆E上的第一象限内,求点C的坐标;
(2)设直线l:x=4,过点A作倾斜角为30°的直线m分别交直线l及椭圆E于点P,Q,求△BPQ的面积S.
(苏州市2012-2013高二 文(下)期末)4.双曲线的渐近线方程为 .
(苏州市2012-2013高二 文(下)期末)18.(本小题满分16分)已知椭圆(a > b > 0)的一个焦点为(,0),且椭圆过点A(,1).
(1)求椭圆的方程;
(2)设M(0,m)(),P是椭圆上的一个动点,求PM 的最大值(用m表示).
(苏州市2013-2014高二 文(下)期末)3.抛物线的准线方程为 .
(苏州市2013-2014高二 文(下)期末)17.(本小题满分14分)如图,在平面直角坐标系xOy中,椭圆的左、右顶点分别为A,B,左、右焦点分别为F1,F2,点在椭圆上,且直线的斜率之积为.
(1)求椭圆的离心率;
(
F
F
x
y
A
B
1
2
M
O
)(2)若点又在以线段F1F2为直径的圆上,且△MAB的面积为, 求椭圆的方程.
(苏州市2014-2015高二 文(下)期末)3.双曲线-=1的离心率为 .
(苏州市2014-2015高二 文(下)期末)18.(本小题满分 16 分)平面直角坐标系 ???????????? 中,已知圆心在第二象限,半径为 2的圆 ???? 与直线????=????相切于坐标原点O,椭圆+=1(????>0)与圆????的一个交点到椭圆的两焦点的距离之和为10.
(1)求圆????的方程;
(2)若圆????上存在一点????(异于坐标原点),满足点????到椭圆右焦点????的距离等于????????的长,试求出点????的坐标.
(苏州市2015-2016(2017-2018)高二 文(下)期末)3.双曲线的离心率为2,则a= .
(苏州市2015-2016(2017-2018)高二 文(下)期末)11.已知过点A(-3,-2)的直线与抛物线C:x2=8y在第二象限相切于点B,记抛物线C的焦点为F,则直线BF的斜率为 .
(苏州市2015-2016(2017-2018)高二 文(下)期末)14.若实数a,b满足,则a的最大值是 .
(苏州市2015-2016(2017-2018)高二 文(下)期末)19.(本小题满分16分)如图,已知椭圆M:的离心率为,且过点.
(1)求椭圆M的标准方程;
(2)设点是椭圆M上异于顶点的任意两点,直线OA,OB的斜率分别为,且.
①求的值;
(
第
19
题图
A
B
C
O
) ②设点B关于x轴的对称点为C,试求直线 AC的斜率.
(苏州市2016-2017高二 文(下)期末)3.在平面直角坐标系xOy中,双曲线-=1的离心率为 .
(苏州市2016-2017高二 文(下)期末)10.在平面直角坐标系xOy中,过抛物线y2=4x的焦点F作弦AB,则●= . (
5
) (
第页共
1
页
)
(苏州市2016-2017高二 文(下)期末)19.在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0),其焦点到相应准线的距离为,离心率为.
(1)求椭圆C的标准方程; (
6
) (
第页共
3
页
)
(2)如图所示A,B是椭圆C上两点,且△AOB的面积为,设射线OA,OB的斜率分别为k1,k2
①求k1●k2的值.
②延长OA到P,使得OP=2OA,且PB交椭圆C于Q,求证为定值.
答案:
直线与圆的方程
4
1<m<121
(x-2)2+(y-1)2=1
5
4
圆锥曲线
7
【答案】
(1)∵2b=4,∴b=2,①
由题意,设A(x,x)(x>0),则,②
AF1F2的面积为2,∴cx=2③,
由①②③得:a=2,椭圆C的方程为:.
(2)设p(x,y),则 F1(-2,0),F2(2,0),
且∠F1PF2是钝角
?PF12+PF22<F1F22?(x+2)2+y2+(x-2)2+y2<32
?x2+y2<8?-<x<.
(1,0)
解(1)因为椭圆的离心率为 ,
所以 a=2c.
又因为椭圆C过点A(2, ),
所以.
由以上结合a2=b2+c2可得:a2=16,b2=4.
所以椭圆的方程为: .
(2)设P(x1,y1),Q(x2,y2)
联立直线与椭圆的方程:
,解得P( ,- ),Q(- , ),
因为点B为椭圆C的下顶点,
所以△BPQ的面积S= ×b×|x1-x2|=
所以△BPQ的面积S为
(1)∵椭圆E:+y2=1的
a=2,b=1,c=,
∴左顶点为A(-2,0),下顶点为B(0,-1).
线段AB的垂直平分线的方程为:y-(-)=2(x+1)
令x=0得它与y轴的交点坐标为(0,),
即圆心在y轴上且过两点A,B的圆的圆心坐标为(0,),
故其半径r=1+=,
∴圆心在y轴上且过两点A,B的圆方程:x2+(y-)2=;
(2)∵△OAP与△OCP的面积相等,
∴P是线段AC的中点,
设C(0,2n),则P(-1,n)代入椭圆的方程得:
+n?2=1,又点A作直线l交椭圆于点P,交y正半轴于点C,故n=,
∴C(0,),又A(-2,0),
直线l的斜率k==
3
17.解:(1)椭圆E中,a2=4,b2=1,c2=3,
F1(-,0),F2(,0),…………………2分
A(-2,0),B(2,0),设C(x,y).
∵∠F1CF290°,∴OC=OF2=.则x2+y2=3.…………………4分
又,∴x2=,y2=.
∵点C在第一象限内,x>0,y>0,
∴,.即C(,).…………………7分
(2)直线AQ方程为:.
与椭圆E方程联立得
, …………………9分
即.∴xQ=.则Q.…………………11分
又, …………………12分
∴△BPQ的面积S=S△ABP-S△ABQ=.…………14分
18.解:(1)由题意,c =,则. ………… 2分
可设椭圆方程为.
∵椭圆过点(,1),∴,解得. ……… 4分
(或由椭圆定义,得,则a = 2,同样得2分)
∴椭圆方程为. ……………… 6分
(2)设,则.
∴. …………… 9分
由,得. …………… 11分
∴当时,在y0 = m时,得PM的最大值为; …………13分
当时,在y0 = 时,得PM的最大值为. ………… 15分
即 ………… 16分
(1),设,则.
, …………… 4分
∵的斜率之积为,.
∵a2 = b2 c2,.
,故椭圆的离心率. …………… 6分
(2)设,则.
由(1)知,,即.① ………… 8分
∵点又在以线段F1F2为直径的圆上,,
而,∴.② ………… 10分
又∵,.③ …………… 12分
由①,②,③,解得.
故椭圆的标准方程为. …………… 14分
1
-
20
19.解(1)由题意,所以,即,
所以椭圆M的方程为, ………………………2分
又因为椭圆M过点,所以,即.
所以所求椭圆M的标准方程为. ………………………4分
(2)①设直线OA的方程为,
化简得,解得, ………………………6分
因为,故,
同理可得, ………………………8分
所以. ………………………10分
②由题意,点B关于x轴的对称点为C的坐标为,
又点是椭圆M上异于顶点的任意两点,
所以,故,即.
………………………12分
设直线AC的斜率为k,则,
因为,即,故,
所以, ………………………15分
所以直线AC的斜率为k为常数,即或. ………………………16分
-3
(
12
) (
第页共
3
页
)
(
13
) (
第页共
1
页
)
