2019年秋人教版七年级数学上册3.1.2 等式的性质课件(共55张PPT)
文档属性
| 名称 | 2019年秋人教版七年级数学上册3.1.2 等式的性质课件(共55张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-08 00:00:00 | ||
图片预览


文档简介
课件55张PPT。3.1 从算式到方程
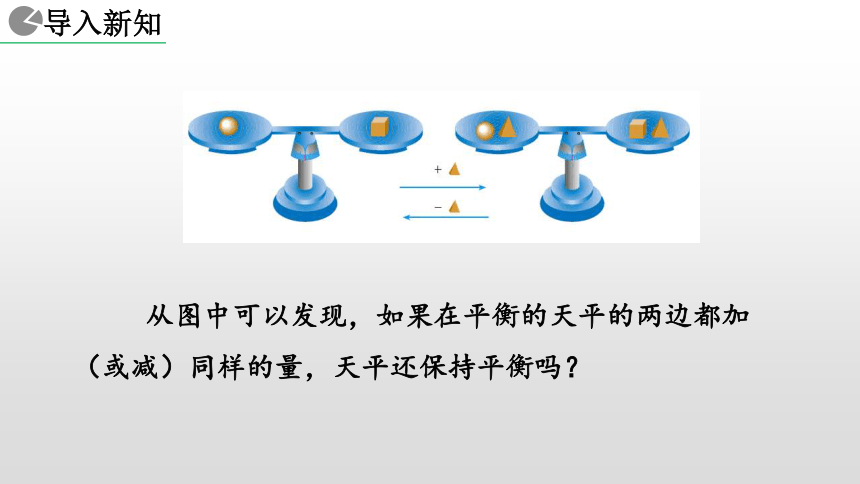
3.1.2 等式的性质 从图中可以发现,如果在平衡的天平的两边都加(或减)同样的量,天平还保持平衡吗?2. 能用等式的性质解简单的一元一次方程.
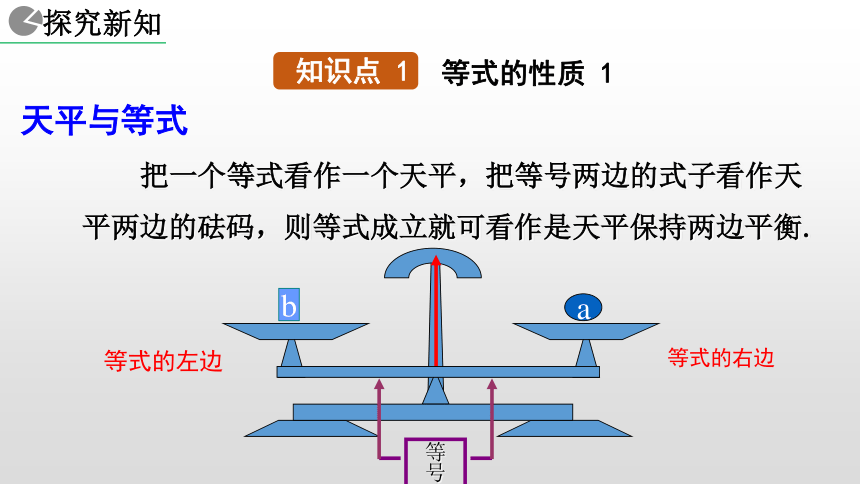
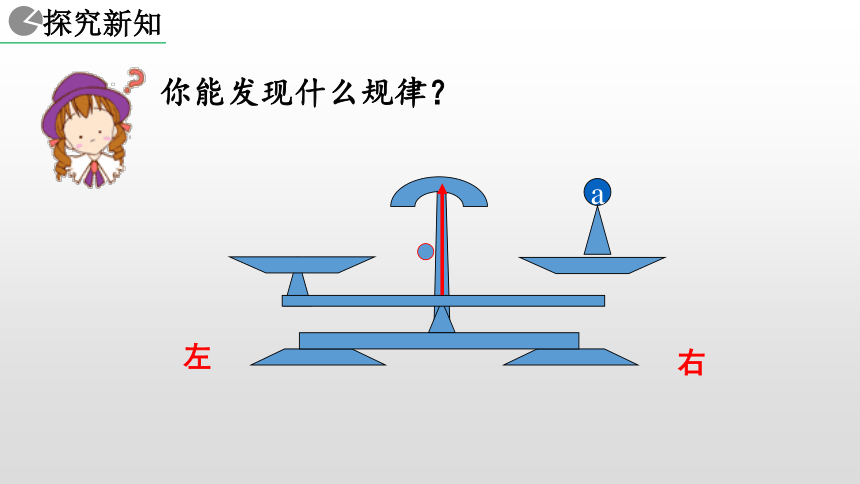
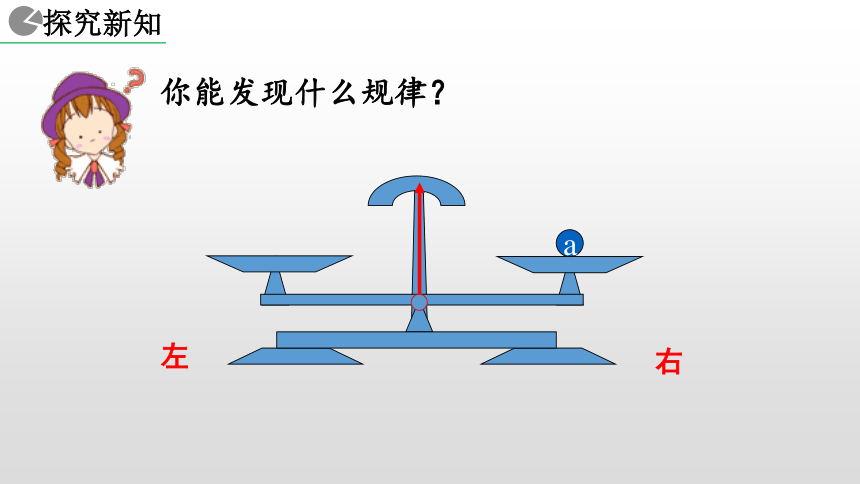
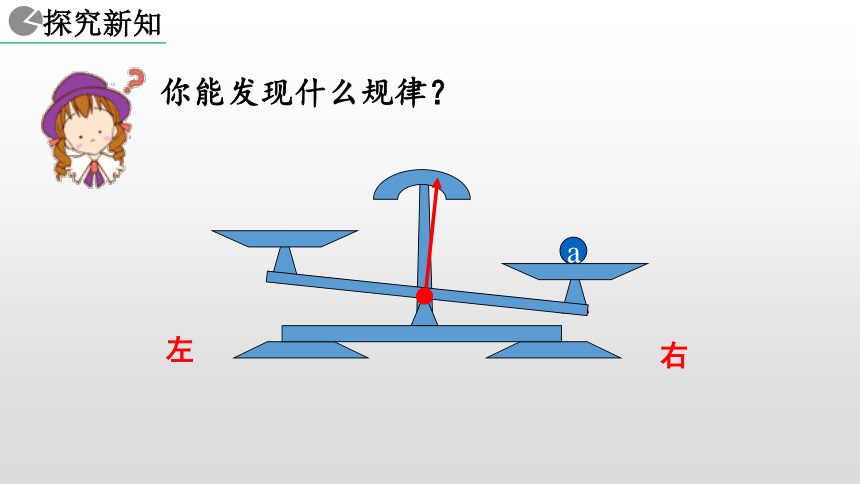
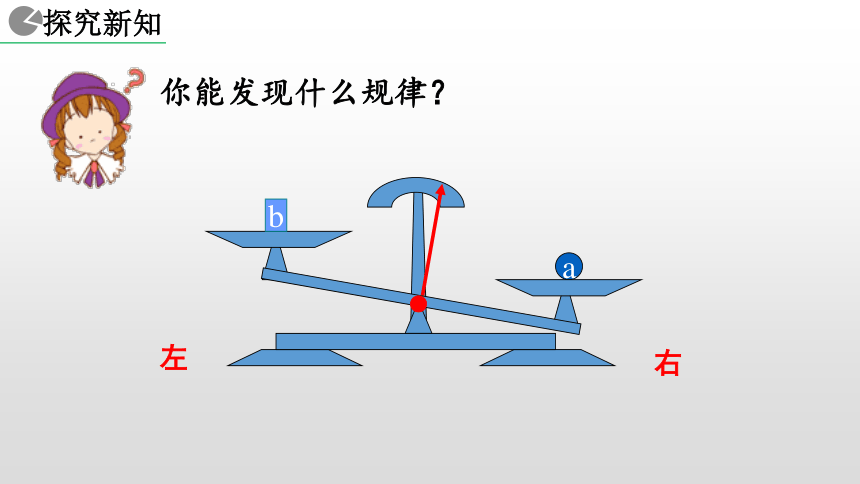
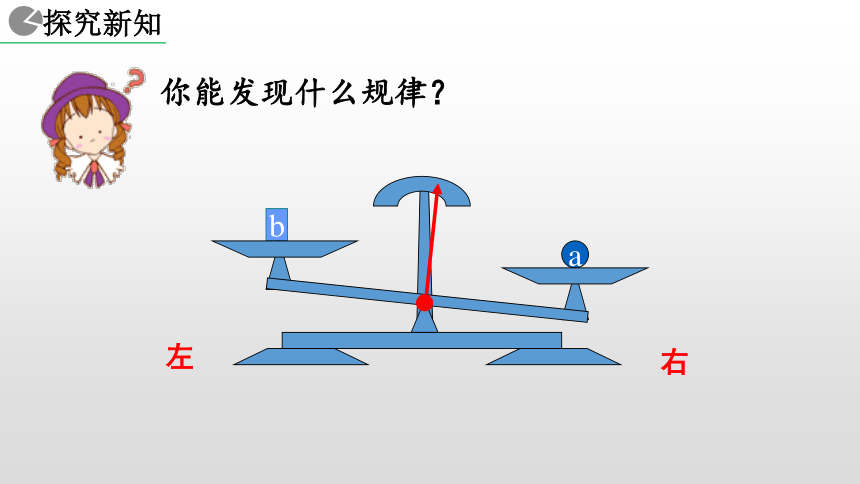
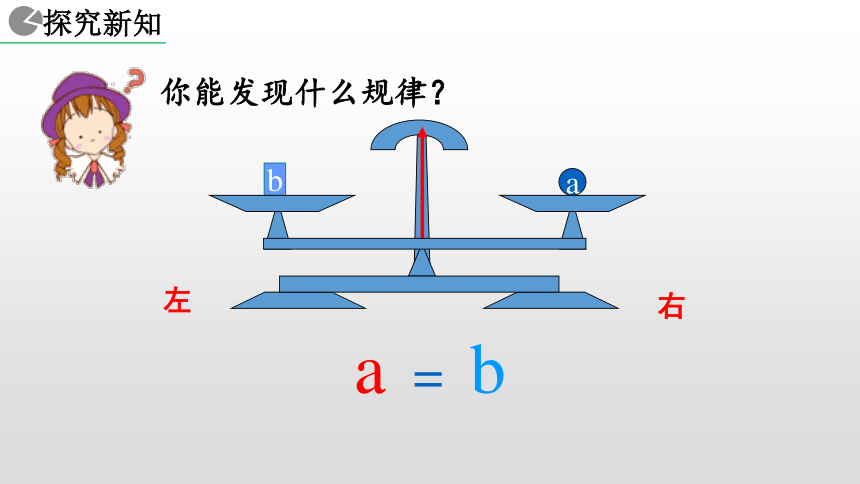
1. 能用文字和数学式子表达等式的两个性质. ba天平与等式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.等式的左边等式的右边等式的性质 1a你能发现什么规律?a右左你能发现什么规律?a右左你能发现什么规律?ab右左你能发现什么规律?ba右左你能发现什么规律?baa = b右左你能发现什么规律?baa = bc右左你能发现什么规律?cbaa = b右左你能发现什么规律?acba = b右左你能发现什么规律?cbcaa = b右左你能发现什么规律?cbcaa = ba+c b+c=右左你能发现什么规律?cca = b右左你能发现什么规律?ca = b右左你能发现什么规律?ca = b右左你能发现什么规律?a = b右左你能发现什么规律?a = ba-c b-c=右左你能发现什么规律?? ? 1+2 = 3 上述两个问题反映出等式具有什么性质? 1+2 = 3 等式的两边同时加上(或减去)同一个数所得的结果仍是等式. ? ? 2x+3x = 5x 2x+3x = 5x 上述两个问题反映出等式具有什么性质? 等式的两边同时加上(或减去)同一个式子,所得的结果仍是等式. 等式的两边同时加上(或减去)同一个数或同一个式子,所得的结果仍是等式. 天平两边同时天平仍然平衡加入拿去相同质量的砝码相同的数 (或式子) 等式两边同时加上减去等式仍然成立换言之,
等式两边同时加 (或减) 同一个数 (或式子),结果仍相等.如果a=b,那么a±c=b±c.等式的性质1在下面的括号内填上适当的数或者式子:1.因为:
所以:2.因为:
所以:3.因为:
所以:想一想、练一练baa = b右左等式的性质 2你能发现什么规律?baa = b右左ab2a = 2b你能发现什么规律?baa = b右左bbaa3a = 3b你能发现什么规律?baa = b右左bbbbbbaaaaaaC个 C个ac = bc你能发现什么规律?ba你能发现什么规律?a = b右左(c≠0)? ? 3m+5m = 8m 3m+5m = 8m 上述两个问题反映出等式具有什么性质? 等式两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .代数式形式等式的性质1.等式两边都要参加运算,且是同一种运算.
2.等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3.等式两边不能都除以0,即0不能作除数或分母.注意识别等式变形的依据例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y ?依据等式的性质1两边同时加5.依据等式的性质1两边同时减3. (2) 怎样从等式 3+x=1 得到等式 x =-2?(3) 怎样从等式 4x=12 得到等式 x =3?(2) 从 a+2=b+2 能不能得到 a=b,为什么?(3) 从-3a=-3b 能不能得到 a=b,为什么?(4) 从 3ac=4a 能不能得到 3c=4,为什么?能,根据等式的性质2,两边同时除以9.能,根据等式的性质1,两边同时加上-2.能,根据等式的性质2,两边同时除以-3.不能,a可能为0.1.指出等式变形的依据.
例2 已知mx=my,下列结论错误的是 ( )
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy解析:根据等式的性质1,可知B、C正确;根据等式的性质2,可知D正确;根据等式的性质2,A选项只有m≠0时才成立,故A错误.A易错提醒:此类判断等式变形是否正确的题型中,尤其注意利用等式的性质2等式两边同除以某个字母,只有这个字母确定不为0时,等式才成立.判断等式变形的对错(1)如果x=y,那么?????????????????? ? (????? )???
(2)如果x=y,那么??????????????????? (????? )
(3)如果x=y,那么 ??????????????????? (????? )
(4)如果x=y,那么??????????????????? (????? )
(5)如果x=y,那么??????????????????? (????? )? 2.判断对错,对的说明根据等式的哪一条性质;错的说出为什么。×√××√左边加右边减,等式不成立当a=5时,无意义两边乘的数不相等等式性质1等式的性质1和性质2利用等式的性质解方程例3 利用等式的性质解下列方程:
(1) x + 7 = 26 解:得: 方程两边同时减去7,x + 7 = 26 = x19小结:解一元一次方程要“化归”为“ x=a ”的形式. (2) -5x = 20 思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ? 化简得: x=-4-5x÷(-5)= 20 ÷(-5)解:方程两边同时加上5
得: 化简得: 方程两边同时 乘-3,得: x =-27思考:对比(1),(3)有什么新特点 ?(3) 一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
例如,将 x = -27 代入方程 的左边, (1) x+6 = 17 ; (2) -3x = 15 ; (3) 2x-1 = -3 ; 解:两边同时加上1,得2x=-2. 两边同时除以2,得x=-1. 两边同时乘以-3,得x=9.3.利用等式的性质解下列方程. 经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.?D1. 下列说法正确的是( ) A. 等式都是方程 B. 方程都是等式 C. 不是方程的就不是等式 D. 未知数的值就是方程的解BAB加3122减y1除以x2解: x=6+5x=11把x=11代入方程的左边,得6,等于右边,所以x=11是方程的解.(2)x=45÷0.3解: x=150把x=150代入方程的左边,得45,等于右边,所以x=150是方程的解.利用等式的性质解下列方程并检验:(1)把 代入方程的左边,得-4,等于右边,所以 是方程的解. (3)5x=-4(4)把x=-4代入方程的左边,得1,等于右边,所以x=-4是方程的解.解:利用等式的性质解下列方程并检验:解:等式的
基本性质基本性质1基本性质2应用1 . 从课后习题中选取;
2 . 完成练习册本课时的习题。
3.1.2 等式的性质 从图中可以发现,如果在平衡的天平的两边都加(或减)同样的量,天平还保持平衡吗?2. 能用等式的性质解简单的一元一次方程.
1. 能用文字和数学式子表达等式的两个性质. ba天平与等式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.等式的左边等式的右边等式的性质 1a你能发现什么规律?a右左你能发现什么规律?a右左你能发现什么规律?ab右左你能发现什么规律?ba右左你能发现什么规律?baa = b右左你能发现什么规律?baa = bc右左你能发现什么规律?cbaa = b右左你能发现什么规律?acba = b右左你能发现什么规律?cbcaa = b右左你能发现什么规律?cbcaa = ba+c b+c=右左你能发现什么规律?cca = b右左你能发现什么规律?ca = b右左你能发现什么规律?ca = b右左你能发现什么规律?a = b右左你能发现什么规律?a = ba-c b-c=右左你能发现什么规律?? ? 1+2 = 3 上述两个问题反映出等式具有什么性质? 1+2 = 3 等式的两边同时加上(或减去)同一个数所得的结果仍是等式. ? ? 2x+3x = 5x 2x+3x = 5x 上述两个问题反映出等式具有什么性质? 等式的两边同时加上(或减去)同一个式子,所得的结果仍是等式. 等式的两边同时加上(或减去)同一个数或同一个式子,所得的结果仍是等式. 天平两边同时天平仍然平衡加入拿去相同质量的砝码相同的数 (或式子) 等式两边同时加上减去等式仍然成立换言之,
等式两边同时加 (或减) 同一个数 (或式子),结果仍相等.如果a=b,那么a±c=b±c.等式的性质1在下面的括号内填上适当的数或者式子:1.因为:
所以:2.因为:
所以:3.因为:
所以:想一想、练一练baa = b右左等式的性质 2你能发现什么规律?baa = b右左ab2a = 2b你能发现什么规律?baa = b右左bbaa3a = 3b你能发现什么规律?baa = b右左bbbbbbaaaaaaC个 C个ac = bc你能发现什么规律?ba你能发现什么规律?a = b右左(c≠0)? ? 3m+5m = 8m 3m+5m = 8m 上述两个问题反映出等式具有什么性质? 等式两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .代数式形式等式的性质1.等式两边都要参加运算,且是同一种运算.
2.等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3.等式两边不能都除以0,即0不能作除数或分母.注意识别等式变形的依据例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y ?依据等式的性质1两边同时加5.依据等式的性质1两边同时减3. (2) 怎样从等式 3+x=1 得到等式 x =-2?(3) 怎样从等式 4x=12 得到等式 x =3?(2) 从 a+2=b+2 能不能得到 a=b,为什么?(3) 从-3a=-3b 能不能得到 a=b,为什么?(4) 从 3ac=4a 能不能得到 3c=4,为什么?能,根据等式的性质2,两边同时除以9.能,根据等式的性质1,两边同时加上-2.能,根据等式的性质2,两边同时除以-3.不能,a可能为0.1.指出等式变形的依据.
例2 已知mx=my,下列结论错误的是 ( )
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy解析:根据等式的性质1,可知B、C正确;根据等式的性质2,可知D正确;根据等式的性质2,A选项只有m≠0时才成立,故A错误.A易错提醒:此类判断等式变形是否正确的题型中,尤其注意利用等式的性质2等式两边同除以某个字母,只有这个字母确定不为0时,等式才成立.判断等式变形的对错(1)如果x=y,那么?????????????????? ? (????? )???
(2)如果x=y,那么??????????????????? (????? )
(3)如果x=y,那么 ??????????????????? (????? )
(4)如果x=y,那么??????????????????? (????? )
(5)如果x=y,那么??????????????????? (????? )? 2.判断对错,对的说明根据等式的哪一条性质;错的说出为什么。×√××√左边加右边减,等式不成立当a=5时,无意义两边乘的数不相等等式性质1等式的性质1和性质2利用等式的性质解方程例3 利用等式的性质解下列方程:
(1) x + 7 = 26 解:得: 方程两边同时减去7,x + 7 = 26 = x19小结:解一元一次方程要“化归”为“ x=a ”的形式. (2) -5x = 20 思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ? 化简得: x=-4-5x÷(-5)= 20 ÷(-5)解:方程两边同时加上5
得: 化简得: 方程两边同时 乘-3,得: x =-27思考:对比(1),(3)有什么新特点 ?(3) 一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
例如,将 x = -27 代入方程 的左边, (1) x+6 = 17 ; (2) -3x = 15 ; (3) 2x-1 = -3 ; 解:两边同时加上1,得2x=-2. 两边同时除以2,得x=-1. 两边同时乘以-3,得x=9.3.利用等式的性质解下列方程. 经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.?D1. 下列说法正确的是( ) A. 等式都是方程 B. 方程都是等式 C. 不是方程的就不是等式 D. 未知数的值就是方程的解BAB加3122减y1除以x2解: x=6+5x=11把x=11代入方程的左边,得6,等于右边,所以x=11是方程的解.(2)x=45÷0.3解: x=150把x=150代入方程的左边,得45,等于右边,所以x=150是方程的解.利用等式的性质解下列方程并检验:(1)把 代入方程的左边,得-4,等于右边,所以 是方程的解. (3)5x=-4(4)把x=-4代入方程的左边,得1,等于右边,所以x=-4是方程的解.解:利用等式的性质解下列方程并检验:解:等式的
基本性质基本性质1基本性质2应用1 . 从课后习题中选取;
2 . 完成练习册本课时的习题。
