2019秋人教版七年级数学上册教学课件:3.2 解一元一次方程(一) 课件(2课时共56张)
文档属性
| 名称 | 2019秋人教版七年级数学上册教学课件:3.2 解一元一次方程(一) 课件(2课时共56张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-06 15:05:57 | ||
图片预览








文档简介
课件56张PPT。3.2 解一元一次方程(一)
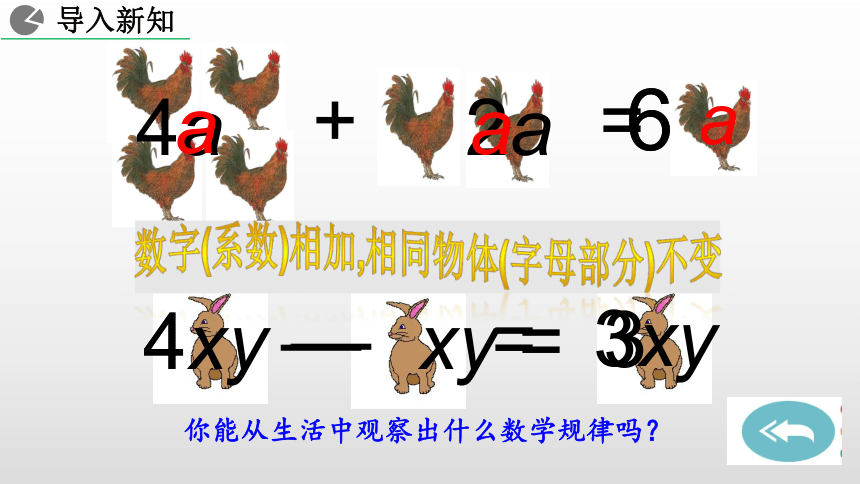
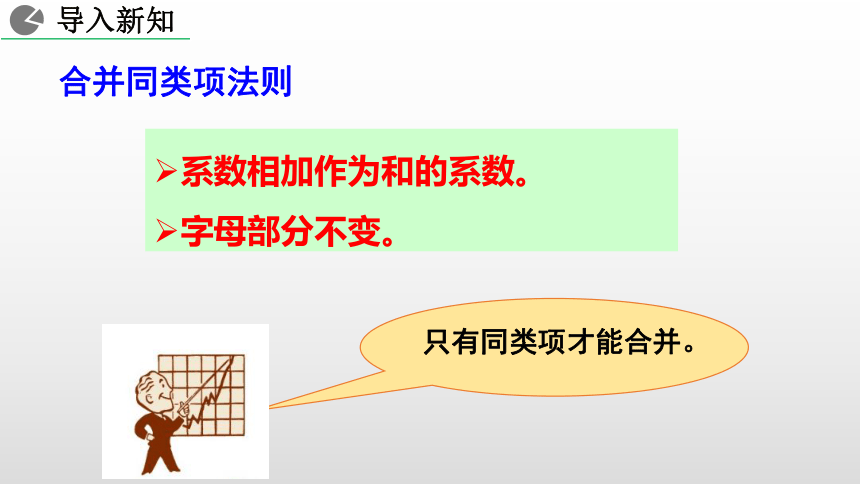
——合并同类项与移项人教版 数学 七年级 上册+ = ― 4a 2a 64xy ― xy =3xya你能从生活中观察出什么数学规律吗?数字(系数)相加,相同物体(字母部分)不变系数相加作为和的系数。
字母部分不变。合并同类项法则 某校三年共购买计算机组140台,去年购买数量是前年的
2倍,今年购买数量又是去年的2倍.前年这个学校购买
了多少台计算机? 设前年这个学校购买了计算机x台,则去年购买计算
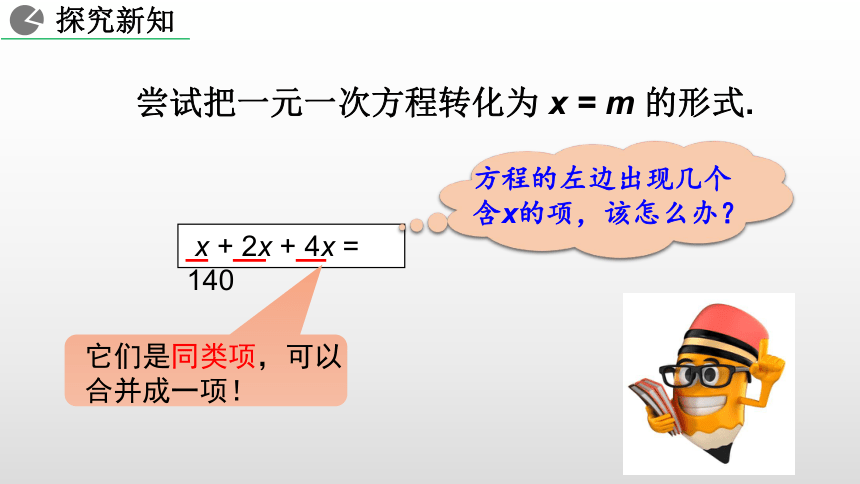
机_____台,今年购买计算机_____台,根据问题中的相等关系 (总量等于各部分量的和) 即:前年购买量+去年购买量+今年购买量=140台列得方程x + 2x +4x = 1402x4x思考:怎样解这个方程呢?1. 会利用合并同类项的方法解一元一次方程,体会等式变形中的化归思想.
2. 能够从实际问题中列出一元一次方程,进一步体会方程模型思想的作用及应用价值.
程大位,明代商人,珠算发明家,历经二十年,于明万历壬辰年(1592年)写就巨著《算法统宗》.《算法统综》搜集了古代流传的595道数学难题并记载了解决方法,堪称中国16—17世纪数学领域集大成的著作.在该书中,有一道“百羊问题”: 甲赶羊群逐草茂,乙拽一羊随其后,
戏问甲及一百否?甲云所说无差谬,
若得这般一群凑,于添半群小半群,
得你一只来方凑,玄机奥妙谁猜透.(注:小半即四分之一)如何解这个方程呢?合并同类项解一元一次方程1.含有相同的_____,并且相同字母的_____也相同的项,叫做同类项;
2.合并同类项时,把各同类项的_____相加减,字母和字母的指数_____.
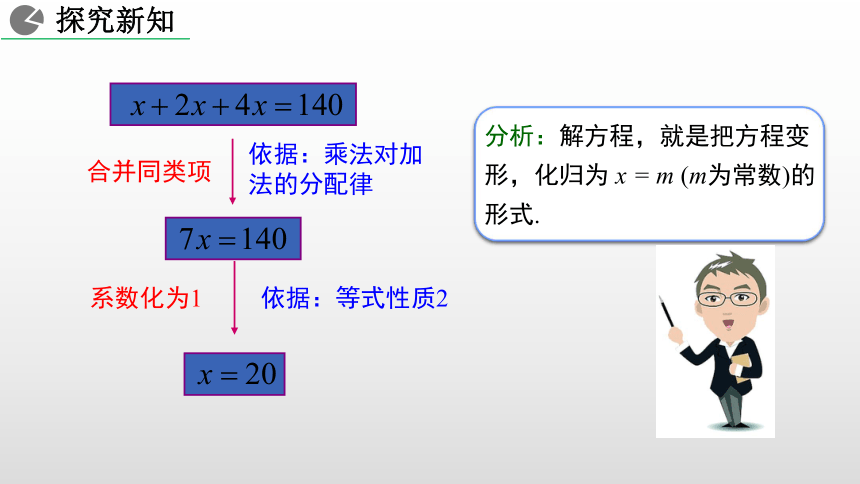
字母指数系数不变-2x4x4y- y x + 2x + 4x = 140尝试把一元一次方程转化为 x = m 的形式.依据:乘法对加法的分配律合并同类项系数化为1依据:等式性质2上述解方程中的“合并”起了什么作用? 解方程中“合并”起了化简作用,把含有未知数的项合并为一项,从而把方程转化为
ax = b的形式,其中a、b是常数,“合并”的依据是逆用分配律.解:合并同类项,得系数化为1,得利用合并同类项解简单的方程解:合并同类项,得系数化为1,得 解下列方程:变式训练解:合并同类项,得系数化为1,得解:合并同类项,得去绝对值,得系数化为1,得x=60 1. 解下列方程:
(1) 5x-2x = 9; (2) .解:合并同类项,得
3x=9,系数化为1,得
x=3.解:合并同类项,得
2x=7,例2 有一列数,按一定规律排列成1,-3,9,-27,81,
-243 ··· . 其中某三个相邻数的和是-1701,这三个数各是
多少?列方程解答实际问题由三个数的和是-1701,得合并同类项,得系数化为1,得答:这三个数是 -243,729,-2187.所以实际问题一元一次方程设未知数 分析实际问题中的数量关系,利用其中的相等关系列出方程,是解决实际问题的一种数学方法.用方程解决实际问题的过程列方程解方程作答解:设这三个数分别是x-1, x, x+1.
根据题意得 (x-1)+x+(x+1)=27
去括号,得 x-1+x+x+1=27
合并同类项得 3x=27
化系数为1得 x=9
x-1=8, x+1=10
答:这三个数分别是8,9,10。
2. 三个连续整数的和等于27,求这三个数. 例3 足球表面是由若干个黑色五边形和白色六边形皮块围成的,黑、白皮块数目的比为3:5,一个足球表面一共有32个皮块,黑色皮块和白色皮块
各有多少个?解:设黑色皮块有3x个,则白色皮块有5x个.
根据题意列方程 3x + 5x = 32,
解得 x = 4,
则黑色皮块有 3x = 12 (个),
白色皮块有 5x = 20 (个).
答:黑色皮块有12个,白色皮块有20个.方法归纳:当题目中出现比例时,一般可通过间接设元,设其中的每一份为x,然后用含x的代数式表示各数量,根据等量关系,列方程求解. 3. 请欣赏一首诗:
太阳下山晚霞红,我把鸭子赶回笼;
一半在外闹哄哄,一半的一半进笼中;
剩下十五围着我,请算多少帮我忙。
你能列出方程来解决这个问题吗?解:设有鸭子x只,依题意,得解得 x=60 答:鸭子有60只. (2018?邵阳)程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,
下列求解结果正确的是( )
A.大和尚25人,小和尚75人 B.大和尚75人,小和尚25人
C.大和尚50人,小和尚50人 D.大、小和尚各100人?A1. 下列方程合并同类项正确的是 ( )
A. 由 3x-x=-1+3,得 2x =4
B. 由 2x+x=-7-4,得 3x =-3
C. 由 15-2=-2x+ x,得 3=x
D. 由 6x-2-4x+2=0,得 2x=0D 3. 某中学七年级(5)班共有学生56人,该班男生的人数是女生人数的2倍少1人.设该班有女生有x人,可列方程为_____________. 2x-1+x=562. 如果2x与x-3的值互为相反数,那么x等于( )
A.-1 B.1 C.-3 D.3 B 解方程:
(1)-3x+0.5x=10. (2)3y-4y=-25-20.
解:合并同类项得
-2.5x=10,
系数化为1,得
x=-4. 解:合并同类项得
-y=-45,
系数化为1,得
y=45. 某洗衣厂2016年计划生产洗衣机25500台,其中Ⅰ型、Ⅱ型、Ⅲ型三种洗衣机的数量之比为1:2:14,这三种洗衣机计划各生产多少台?答:计划生产Ⅰ型洗衣机1500台,Ⅱ型洗衣机3000台,Ⅲ型洗衣机21000台.解:设计划生产Ⅰ型洗衣机x台,则计划生产Ⅱ型洗衣机2x台,Ⅲ型洗衣机14x台,依题意,得x+2x+14x=25500,解得x=1500,则2x=3000,14x=21000.3x+x+5x=180合并同类项系数化为1等式的性质2理论依据?9x=140x=20 希腊数学家丢番图(公元3~4世纪)的墓碑上记载着: 根据以上信息,你知道丢番图活了多少岁吗?“他的生命的六分之一是幸福童年;再活了他生命的十二分之一,两颊长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他有了儿子,感到很幸福;可是儿子只活了他父亲年龄的一半;儿子死后,他在极悲痛中度过了四年,也与世长辞了.”1. 进一步认识解方程的基本变形——移项,感悟解方程过程中的转化思想.
2. 会用移项、合并同类项解ax+b=cx+d型的方程.
3. 能通过分析问题找到相等关系并通过列方程解决问题.2. 观察下列一元一次方程,与上题的类型有什么区别?【想一想】怎样才能使它向 x=a (a为常数)的形式转化呢?利用移项解一元一次方程把一些图书分给某班同学阅读,如果每人3本,则剩余20本;若每人4本,则还缺少25本,这个班的学生有多少人? 分析:设这个班有x名学生.这批书共有(3x+20)本.这批书共有(4x-25)本.表示同一个量的两个不同的式子相等.
(即:这批书的总数是一个定值)3x+20=4x-25思考:怎样解这个方程呢?请运用等式的性质解下列方程:(1) 4x-15 = 9;
解:两边都加15,得
4x-15+15 = 9 +15
合并同类项,得
4x = 24.
系数化为1,得
x = 6.即 4x = 9 +15. “-15”这项移动后,从方程的左边移到了方程的右边.(1) 4x-15 = 9 ① 4x = 9 +15 ② 观察方程①到方程②的变形过程,说一说有改变的是哪一项?它有哪些变化?“-15”这一项符号由“-”变“+”(2) 2x = 5x -21.
解:两边都减5x,得
2x = 5x-21 -5x -5x 2x-5x = -21. 合并同类项,得
-3x = -21.系数化为1,得
x = 7.(2) 2x = 5x -21 ③ 2x- 5x = -21 ④ 一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项. 移项的定义下列方程的变形,属于移项的是( )
A.由 -3x=24得x=-8
B.由 3x+6-2x=8 得 3x-2x+6=8
C.由4x+5=0 得-4x-5=0
D.由2x+1=0得 2x=-1D下列移项正确的是 ( )
A. 由2+x=8,得到x=8+2
B. 由5x=-8+x,得到5x+x= -8
C. 由4x=2x+1,得到4x-2x=1
D. 由5x-3=0,得到5x=-3C做一做例1 解下列方程: 解:移项,得合并同类项 ,得系数化为1,得利用移项解一元一次方程(1)解:移项,得合并同类项,得系数化为1,得解一元一次方程ax+b=cx+d(a,b,c,d均为常数,且a≠c)的一般步骤:ax-cx=d-b移项合并同类项系数化为1(a-c)x=d-b1. 解下列方程:(1) 5x-7=2x-10;(2) -0.3x+3=9+1.2x.解:移项,得5x-2x=-10+7,合并同类项,得3x=-3,系数化为1, 得x=-1.解:移项,得-0.3x-1.2x=9-3,合并同类项,得-1.5x=6,系数化为1,得x=-4.列方程解答实际问题例2 某制药厂制造一批药品,如果用旧工艺,则废水排量要比环保限制的最大量还多200 t;如果用新工艺,则废水排量要比环保限制的最大量少100 t.新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?旧工艺废水排量-200吨=新工艺排水量+100吨解:若设新工艺的废水排量为2x t,则旧工艺的废水排量为5x t.由题意得移项,得5x-2x=100+200,系数化为1,得x=100, 合并同类项,得3x=300,答:新工艺的废水排量为 200 t,旧工艺的废水排量为?500?t.5x-200=2x+100,所以2x=200,5x=500.我区期末考试一次数学阅卷中,阅B卷第28题(简称B28)的教师人数是阅A卷第18题(简称A18)教师人数的3倍,在阅卷过程中,由于情况变化,需要从阅B28题中调12人到A18阅卷,调动后阅B28剩下的人数比原先阅A18人数的一半还多3人,求阅B28题和阅A18题的原有教师人数各为多少?变式训练调动前:阅B28题的教师人数=3×阅A18题的教师人数调动后:阅B28题的教师人数-12=原阅A18题的教师人数÷2+3解:设原有教师x人阅A18题,则原有教师3x人阅B28题,所以 3x=18.答:阅A18题原有教师6人,阅B28题原有教师18人.2. 下面是两种移动电话计费方式: 问:一个月内,通话时间是多少分钟时,两种移动电话计费方式的费用一样?解:设通话时间t分钟,则按方式一要收费(50+0.3t)元,
按方式二要收费(10+0.4t). 如果两种移动电话 计费方式的费用一样,
则 50+0.3t= 10+0.4t.
移项,得 0.3t- 0.4t =10-50.
合并同类项,得 -0.1t =-40.
系数化为1,得 t =400.
答:一个月内通话400分钟时,两种计费方式的 费用一样. (2018?张家界)列方程解应用题.
《九章算术》中有“盈不足术”的问题,原文如下:
“今有共買羊,人出五,不足四十五;人出七,不足三.问人数、羊價各幾何?”
题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元.求人数和羊价各是多少? 解:设买羊为x人,则羊价为(5x+45)元,
5x+45=7x+3,
x=21,
5×21+45=150(元),
答:买羊人数为21人,羊价为150元.1.下列变形属于移项且正确的是( )
A.由2x-3y+5=0,得5-3y+2x=0
B.由3x-2=5x+1,得3x-5x=1+2
C.由2x-5=7x+1,得2x+7x=1-5
D.由3x-5=-3x,得-3x-5-3x=0B2. 对方程4x-5=6x-7-3x进行变形正确的是( )
A.4x=6x+5+7-3x
B.4x-6x+3x=5-7
C.4x-6x-3x=5-7
D.4x-6x+3x=-5-7B5. 当x =_____时,式子 2x-1 的值比式子 5x+6 的值小1.3. 已知 2m-3=3n+1,则 2m-3n = .4-2解下列一元一次方程:解: (1) x =-2; (2) t =20;
(3) x =-4; (4) x =2. 有一些分别标有3,6,9,12…的卡片,后一张卡片上的数比前一张卡片上的数大3,从中任意拿相邻的三张卡片,若它们上面的数之和为108,则拿到的是哪三张卡片?解:设这张卡片中最小的一个数为x,则另两个数分别为x+3、x+6,
依题意列方程,得 x+x+3+x+6=108,
解得 x=33,
所以 x+3=36,x+6=39.
故这三张卡片上面的数分别是33,36,39.移项解一元一次方程定义 步骤应用注意:移项一定要变号移项合并同类项系数化为11 . 从课后习题中选取;
2 . 完成练习册本课时的习题。
——合并同类项与移项人教版 数学 七年级 上册+ = ― 4a 2a 64xy ― xy =3xya你能从生活中观察出什么数学规律吗?数字(系数)相加,相同物体(字母部分)不变系数相加作为和的系数。
字母部分不变。合并同类项法则 某校三年共购买计算机组140台,去年购买数量是前年的
2倍,今年购买数量又是去年的2倍.前年这个学校购买
了多少台计算机? 设前年这个学校购买了计算机x台,则去年购买计算
机_____台,今年购买计算机_____台,根据问题中的相等关系 (总量等于各部分量的和) 即:前年购买量+去年购买量+今年购买量=140台列得方程x + 2x +4x = 1402x4x思考:怎样解这个方程呢?1. 会利用合并同类项的方法解一元一次方程,体会等式变形中的化归思想.
2. 能够从实际问题中列出一元一次方程,进一步体会方程模型思想的作用及应用价值.
程大位,明代商人,珠算发明家,历经二十年,于明万历壬辰年(1592年)写就巨著《算法统宗》.《算法统综》搜集了古代流传的595道数学难题并记载了解决方法,堪称中国16—17世纪数学领域集大成的著作.在该书中,有一道“百羊问题”: 甲赶羊群逐草茂,乙拽一羊随其后,
戏问甲及一百否?甲云所说无差谬,
若得这般一群凑,于添半群小半群,
得你一只来方凑,玄机奥妙谁猜透.(注:小半即四分之一)如何解这个方程呢?合并同类项解一元一次方程1.含有相同的_____,并且相同字母的_____也相同的项,叫做同类项;
2.合并同类项时,把各同类项的_____相加减,字母和字母的指数_____.
字母指数系数不变-2x4x4y- y x + 2x + 4x = 140尝试把一元一次方程转化为 x = m 的形式.依据:乘法对加法的分配律合并同类项系数化为1依据:等式性质2上述解方程中的“合并”起了什么作用? 解方程中“合并”起了化简作用,把含有未知数的项合并为一项,从而把方程转化为
ax = b的形式,其中a、b是常数,“合并”的依据是逆用分配律.解:合并同类项,得系数化为1,得利用合并同类项解简单的方程解:合并同类项,得系数化为1,得 解下列方程:变式训练解:合并同类项,得系数化为1,得解:合并同类项,得去绝对值,得系数化为1,得x=60 1. 解下列方程:
(1) 5x-2x = 9; (2) .解:合并同类项,得
3x=9,系数化为1,得
x=3.解:合并同类项,得
2x=7,例2 有一列数,按一定规律排列成1,-3,9,-27,81,
-243 ··· . 其中某三个相邻数的和是-1701,这三个数各是
多少?列方程解答实际问题由三个数的和是-1701,得合并同类项,得系数化为1,得答:这三个数是 -243,729,-2187.所以实际问题一元一次方程设未知数 分析实际问题中的数量关系,利用其中的相等关系列出方程,是解决实际问题的一种数学方法.用方程解决实际问题的过程列方程解方程作答解:设这三个数分别是x-1, x, x+1.
根据题意得 (x-1)+x+(x+1)=27
去括号,得 x-1+x+x+1=27
合并同类项得 3x=27
化系数为1得 x=9
x-1=8, x+1=10
答:这三个数分别是8,9,10。
2. 三个连续整数的和等于27,求这三个数. 例3 足球表面是由若干个黑色五边形和白色六边形皮块围成的,黑、白皮块数目的比为3:5,一个足球表面一共有32个皮块,黑色皮块和白色皮块
各有多少个?解:设黑色皮块有3x个,则白色皮块有5x个.
根据题意列方程 3x + 5x = 32,
解得 x = 4,
则黑色皮块有 3x = 12 (个),
白色皮块有 5x = 20 (个).
答:黑色皮块有12个,白色皮块有20个.方法归纳:当题目中出现比例时,一般可通过间接设元,设其中的每一份为x,然后用含x的代数式表示各数量,根据等量关系,列方程求解. 3. 请欣赏一首诗:
太阳下山晚霞红,我把鸭子赶回笼;
一半在外闹哄哄,一半的一半进笼中;
剩下十五围着我,请算多少帮我忙。
你能列出方程来解决这个问题吗?解:设有鸭子x只,依题意,得解得 x=60 答:鸭子有60只. (2018?邵阳)程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,
下列求解结果正确的是( )
A.大和尚25人,小和尚75人 B.大和尚75人,小和尚25人
C.大和尚50人,小和尚50人 D.大、小和尚各100人?A1. 下列方程合并同类项正确的是 ( )
A. 由 3x-x=-1+3,得 2x =4
B. 由 2x+x=-7-4,得 3x =-3
C. 由 15-2=-2x+ x,得 3=x
D. 由 6x-2-4x+2=0,得 2x=0D 3. 某中学七年级(5)班共有学生56人,该班男生的人数是女生人数的2倍少1人.设该班有女生有x人,可列方程为_____________. 2x-1+x=562. 如果2x与x-3的值互为相反数,那么x等于( )
A.-1 B.1 C.-3 D.3 B 解方程:
(1)-3x+0.5x=10. (2)3y-4y=-25-20.
解:合并同类项得
-2.5x=10,
系数化为1,得
x=-4. 解:合并同类项得
-y=-45,
系数化为1,得
y=45. 某洗衣厂2016年计划生产洗衣机25500台,其中Ⅰ型、Ⅱ型、Ⅲ型三种洗衣机的数量之比为1:2:14,这三种洗衣机计划各生产多少台?答:计划生产Ⅰ型洗衣机1500台,Ⅱ型洗衣机3000台,Ⅲ型洗衣机21000台.解:设计划生产Ⅰ型洗衣机x台,则计划生产Ⅱ型洗衣机2x台,Ⅲ型洗衣机14x台,依题意,得x+2x+14x=25500,解得x=1500,则2x=3000,14x=21000.3x+x+5x=180合并同类项系数化为1等式的性质2理论依据?9x=140x=20 希腊数学家丢番图(公元3~4世纪)的墓碑上记载着: 根据以上信息,你知道丢番图活了多少岁吗?“他的生命的六分之一是幸福童年;再活了他生命的十二分之一,两颊长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他有了儿子,感到很幸福;可是儿子只活了他父亲年龄的一半;儿子死后,他在极悲痛中度过了四年,也与世长辞了.”1. 进一步认识解方程的基本变形——移项,感悟解方程过程中的转化思想.
2. 会用移项、合并同类项解ax+b=cx+d型的方程.
3. 能通过分析问题找到相等关系并通过列方程解决问题.2. 观察下列一元一次方程,与上题的类型有什么区别?【想一想】怎样才能使它向 x=a (a为常数)的形式转化呢?利用移项解一元一次方程把一些图书分给某班同学阅读,如果每人3本,则剩余20本;若每人4本,则还缺少25本,这个班的学生有多少人? 分析:设这个班有x名学生.这批书共有(3x+20)本.这批书共有(4x-25)本.表示同一个量的两个不同的式子相等.
(即:这批书的总数是一个定值)3x+20=4x-25思考:怎样解这个方程呢?请运用等式的性质解下列方程:(1) 4x-15 = 9;
解:两边都加15,得
4x-15+15 = 9 +15
合并同类项,得
4x = 24.
系数化为1,得
x = 6.即 4x = 9 +15. “-15”这项移动后,从方程的左边移到了方程的右边.(1) 4x-15 = 9 ① 4x = 9 +15 ② 观察方程①到方程②的变形过程,说一说有改变的是哪一项?它有哪些变化?“-15”这一项符号由“-”变“+”(2) 2x = 5x -21.
解:两边都减5x,得
2x = 5x-21 -5x -5x 2x-5x = -21. 合并同类项,得
-3x = -21.系数化为1,得
x = 7.(2) 2x = 5x -21 ③ 2x- 5x = -21 ④ 一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项. 移项的定义下列方程的变形,属于移项的是( )
A.由 -3x=24得x=-8
B.由 3x+6-2x=8 得 3x-2x+6=8
C.由4x+5=0 得-4x-5=0
D.由2x+1=0得 2x=-1D下列移项正确的是 ( )
A. 由2+x=8,得到x=8+2
B. 由5x=-8+x,得到5x+x= -8
C. 由4x=2x+1,得到4x-2x=1
D. 由5x-3=0,得到5x=-3C做一做例1 解下列方程: 解:移项,得合并同类项 ,得系数化为1,得利用移项解一元一次方程(1)解:移项,得合并同类项,得系数化为1,得解一元一次方程ax+b=cx+d(a,b,c,d均为常数,且a≠c)的一般步骤:ax-cx=d-b移项合并同类项系数化为1(a-c)x=d-b1. 解下列方程:(1) 5x-7=2x-10;(2) -0.3x+3=9+1.2x.解:移项,得5x-2x=-10+7,合并同类项,得3x=-3,系数化为1, 得x=-1.解:移项,得-0.3x-1.2x=9-3,合并同类项,得-1.5x=6,系数化为1,得x=-4.列方程解答实际问题例2 某制药厂制造一批药品,如果用旧工艺,则废水排量要比环保限制的最大量还多200 t;如果用新工艺,则废水排量要比环保限制的最大量少100 t.新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?旧工艺废水排量-200吨=新工艺排水量+100吨解:若设新工艺的废水排量为2x t,则旧工艺的废水排量为5x t.由题意得移项,得5x-2x=100+200,系数化为1,得x=100, 合并同类项,得3x=300,答:新工艺的废水排量为 200 t,旧工艺的废水排量为?500?t.5x-200=2x+100,所以2x=200,5x=500.我区期末考试一次数学阅卷中,阅B卷第28题(简称B28)的教师人数是阅A卷第18题(简称A18)教师人数的3倍,在阅卷过程中,由于情况变化,需要从阅B28题中调12人到A18阅卷,调动后阅B28剩下的人数比原先阅A18人数的一半还多3人,求阅B28题和阅A18题的原有教师人数各为多少?变式训练调动前:阅B28题的教师人数=3×阅A18题的教师人数调动后:阅B28题的教师人数-12=原阅A18题的教师人数÷2+3解:设原有教师x人阅A18题,则原有教师3x人阅B28题,所以 3x=18.答:阅A18题原有教师6人,阅B28题原有教师18人.2. 下面是两种移动电话计费方式: 问:一个月内,通话时间是多少分钟时,两种移动电话计费方式的费用一样?解:设通话时间t分钟,则按方式一要收费(50+0.3t)元,
按方式二要收费(10+0.4t). 如果两种移动电话 计费方式的费用一样,
则 50+0.3t= 10+0.4t.
移项,得 0.3t- 0.4t =10-50.
合并同类项,得 -0.1t =-40.
系数化为1,得 t =400.
答:一个月内通话400分钟时,两种计费方式的 费用一样. (2018?张家界)列方程解应用题.
《九章算术》中有“盈不足术”的问题,原文如下:
“今有共買羊,人出五,不足四十五;人出七,不足三.问人数、羊價各幾何?”
题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元.求人数和羊价各是多少? 解:设买羊为x人,则羊价为(5x+45)元,
5x+45=7x+3,
x=21,
5×21+45=150(元),
答:买羊人数为21人,羊价为150元.1.下列变形属于移项且正确的是( )
A.由2x-3y+5=0,得5-3y+2x=0
B.由3x-2=5x+1,得3x-5x=1+2
C.由2x-5=7x+1,得2x+7x=1-5
D.由3x-5=-3x,得-3x-5-3x=0B2. 对方程4x-5=6x-7-3x进行变形正确的是( )
A.4x=6x+5+7-3x
B.4x-6x+3x=5-7
C.4x-6x-3x=5-7
D.4x-6x+3x=-5-7B5. 当x =_____时,式子 2x-1 的值比式子 5x+6 的值小1.3. 已知 2m-3=3n+1,则 2m-3n = .4-2解下列一元一次方程:解: (1) x =-2; (2) t =20;
(3) x =-4; (4) x =2. 有一些分别标有3,6,9,12…的卡片,后一张卡片上的数比前一张卡片上的数大3,从中任意拿相邻的三张卡片,若它们上面的数之和为108,则拿到的是哪三张卡片?解:设这张卡片中最小的一个数为x,则另两个数分别为x+3、x+6,
依题意列方程,得 x+x+3+x+6=108,
解得 x=33,
所以 x+3=36,x+6=39.
故这三张卡片上面的数分别是33,36,39.移项解一元一次方程定义 步骤应用注意:移项一定要变号移项合并同类项系数化为11 . 从课后习题中选取;
2 . 完成练习册本课时的习题。
