2.2.1_2.2.2直线与平面平行的判定平面与平面平行的判定课件(30张)
文档属性
| 名称 | 2.2.1_2.2.2直线与平面平行的判定平面与平面平行的判定课件(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 13:24:27 | ||
图片预览







文档简介
课件30张PPT。2.2 直线、平面平行的判定及其性质2.2.1~2.2.2 直线与平面平行的判定
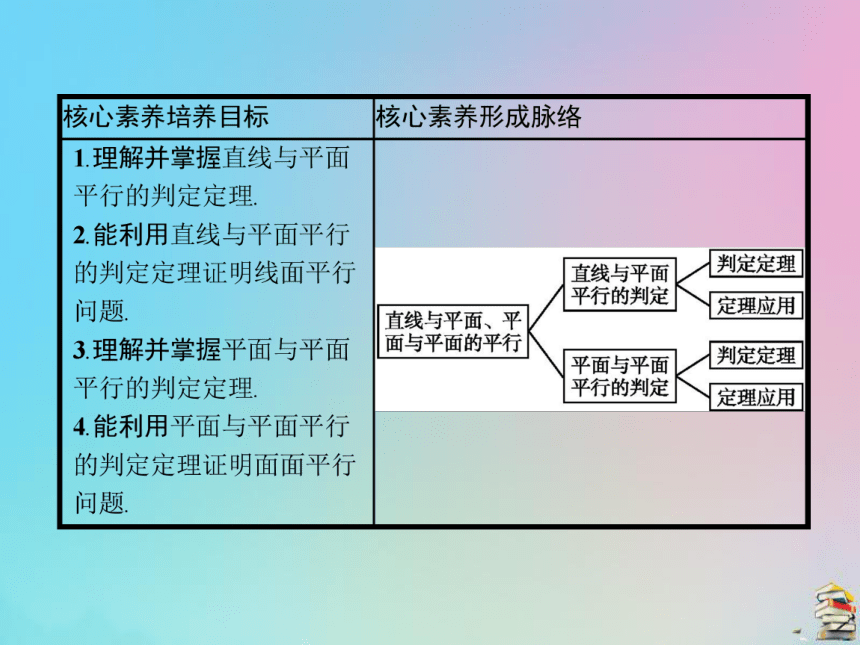
平面与平面平行的判定一二一、直线与平面平行的判定定理
1.如图,将课本ABCD的一边AB紧贴桌面α,把课本绕AB转动,在转动过程中,AB的对边CD(不落在α内)和平面α有何位置关系?
提示:因为没有公共点,所以CD∥α. 一二2.填表:直线与平面平行的判定定理 3.做一做:能保证直线a与平面α平行的条件是( )
A.b?α,a∥b
B.b?α,c∥α,a∥b,a∥c
C.b?α,A,B∈a,C,D∈b,且AC∥BD
D.a?α,b?α,a∥b
答案:D一二二、平面与平面平行的判定定理
1.三角板的一条边所在直线与平面α平行,这个三角板所在平面与α平行吗?
提示:不一定平行.
2.三角板的两条边所在直线分别与平面α平行,这个三角板所在平面与α平行吗?
提示:平行.
3.如图,平面BCC1B1内有多少条直线与平面ABCD平行?这两个平面平行吗?
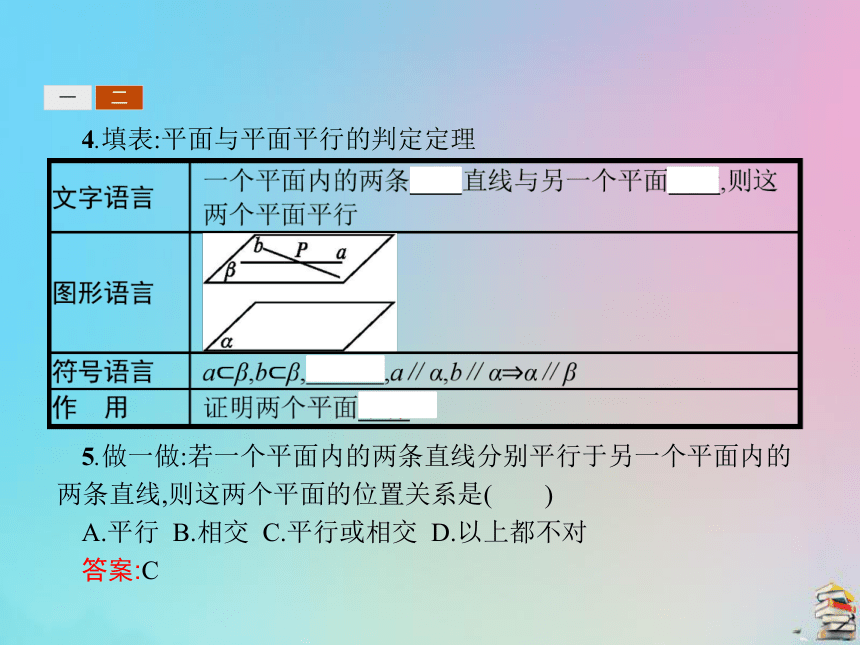
提示:无数条,不平行.一二4.填表:平面与平面平行的判定定理 5.做一做:若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )
A.平行 B.相交 C.平行或相交 D.以上都不对
答案:C一二6.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)如果一条直线和一个平面内的另一条直线平行,那么这条直线和这个平面平行. ( )
(2)如果一个平面内有两条直线和另一个平面平行,那么这两个平面平行. ( )
(3)如果一个平面内有无数条直线和另一个平面平行,那么这两个平面平行. ( )
答案:(1)× (2)× (3)×探究一探究二探究三思维辨析直线与平面平行的判定
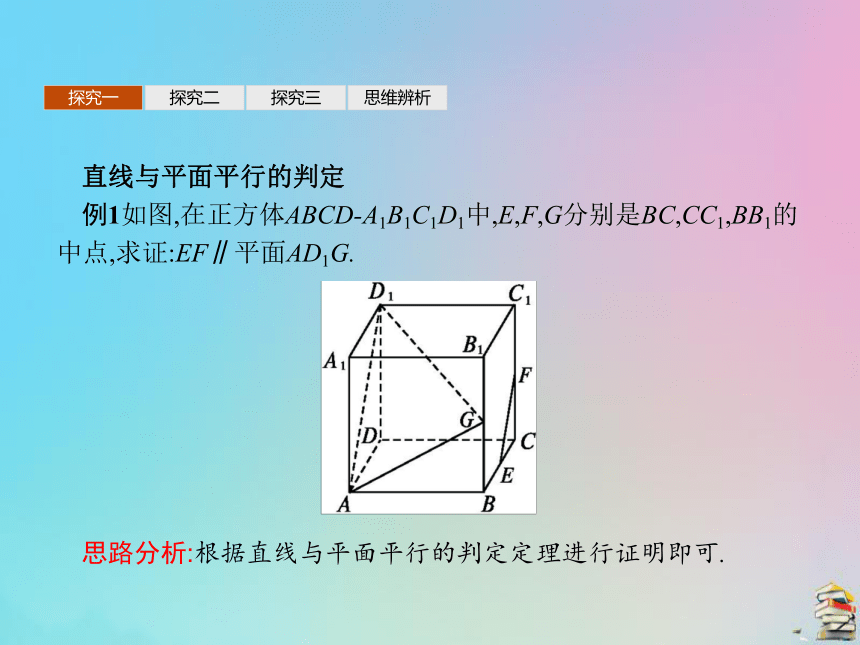
例1如图,在正方体ABCD-A1B1C1D1中,E,F,G分别是BC,CC1,BB1的中点,求证:EF∥平面AD1G.思路分析:根据直线与平面平行的判定定理进行证明即可. 探究一探究二探究三思维辨析证明连接BC1,则由E,F分别是BC,CC1的中点知,EF∥BC1.
又AB??A1B1??D1C1,
所以四边形ABC1D1是平行四边形,
所以BC1∥AD1,所以EF∥AD1.
又EF?平面AD1G,AD1?平面AD1G,
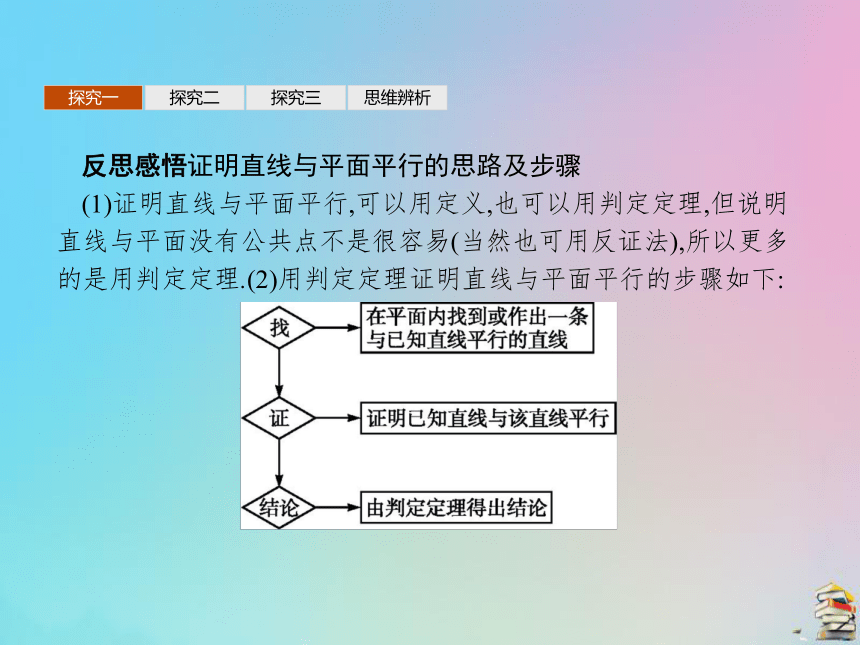
所以EF∥平面AD1G.探究一探究二探究三思维辨析反思感悟证明直线与平面平行的思路及步骤
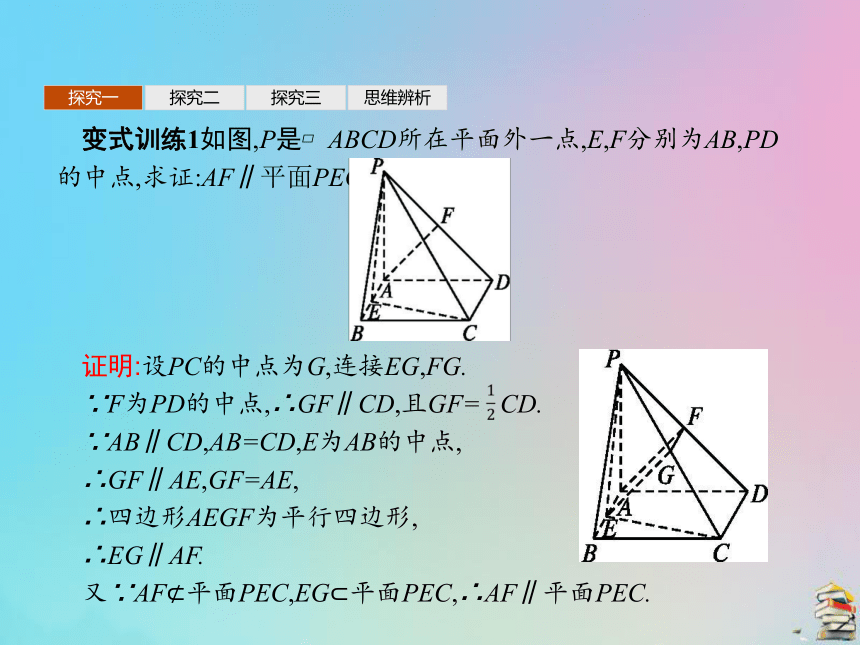
(1)证明直线与平面平行,可以用定义,也可以用判定定理,但说明直线与平面没有公共点不是很容易(当然也可用反证法),所以更多的是用判定定理.(2)用判定定理证明直线与平面平行的步骤如下:探究一探究二探究三思维辨析变式训练1如图,P是?ABCD所在平面外一点,E,F分别为AB,PD的中点,求证:AF∥平面PEC.
证明:设PC的中点为G,连接EG,FG.
∵F为PD的中点,∴GF∥CD,且GF= CD.
∵AB∥CD,AB=CD,E为AB的中点,
∴GF∥AE,GF=AE,
∴四边形AEGF为平行四边形,
∴EG∥AF.
又∵AF?平面PEC,EG?平面PEC,∴AF∥平面PEC.探究一探究二探究三思维辨析平面与平面平行的判定
例2如图所示,在正方体ABCD-A1B1C1D1中,M,E,F,N分别是A1B1,B1C1,C1D1,D1A1的中点,求证:
(1)E,F,B,D四点共面;
(2)平面MAN∥平面EFDB.
思路分析:(1)只需证明BD∥EF,即可证明E,F,B,D共面.(2)要证平面MAN∥平面EFDB,只需证MN∥平面EFDB,AM∥平面EFDB.探究一探究二探究三思维辨析证明:(1)连接B1D1.
∵E,F分别是B1C1和C1D1的中点,
∴EF∥B1D1.而BD∥B1D1,
∴BD∥EF.∴E,F,B,D四点共面.
(2)由题意知MN∥B1D1,B1D1∥BD,
∴MN∥BD.
而MN?平面EFDB,
∴MN∥平面EFDB,连接MF.
∵点M,F分别是A1B1与C1D1的中点,∴MF??AD.
∴四边形ADFM是平行四边形.∴AM∥DF.
∵AM?平面EFDB,DF?平面EFDB,∴AM∥平面EFDB.又AM∩MN=M,∴平面MAN∥平面EFDB.探究一探究二探究三思维辨析反思感悟证明平面与平面平行的思路及步骤
(1)证明两个平面平行,可以用定义,也可以用判定定理.但用定义证明时,需说明两个平面没有公共点,这一点也不容易做到(可用反证法).
(2)用判定定理证明两个平面平行,其步骤如下:探究一探究二探究三思维辨析延伸探究本例中,设P是棱AA1的中点,其他条件不变,求证:平面PMN∥平面C1BD.
证明:连接AB1.
∵P,M分别是AA1,A1B1的中点,∴PM∥AB1.
又AB1∥C1D,∴PM∥C1D.
又PM?平面C1BD,C1D?平面C1BD,∴PM∥平面C1BD.
同理MN∥平面C1BD.又PM∩MN=M,
∴平面PMN∥平面C1BD.探究一探究二探究三思维辨析线面平行、面面平行判定定理的综合
例3如图,四边形ABCD是平行四边形,点E,F,G分别为线段BC,PB,AD的中点.
(1)求证:EF∥平面PAC;
(2)求证:平面PCG∥平面AEF;
(3)在线段BD上找一点H,使得FH∥平面PCG,并说明理由.探究一探究二探究三思维辨析(1)证明∵E,F分别是BC,BP中点,
∵PC?平面PAC,EF?平面PAC,
∴EF∥平面PAC.
(2)证明∵E,G分别是BC,AD中点,
∴AE∥CG,
∵AE?平面PCG,CG?平面PCG,
∴AE∥平面PCG,
又∵EF∥PC,
PC?平面PCG,EF?平面PCG,
∴EF∥平面PCG,
AE∩EF=E,AE,EF?平面AEF,
∴平面AEF∥平面PCG.探究一探究二探究三思维辨析(3)解设AE,GC与BD分别交于M,N两点,
由(2)知,平面PCG∥平面AEF.
∵点F,M在平面AEF上,连接点F,点M,
则FM?平面AEF,且FM?平面PCG.
∴FM∥平面PCG,
即M点为所找的H点.
反思感悟探索型问题的常见类型
常见的有以下两类:条件探索型和结论探索型.条件探索型问题是针对一个结论,条件未知需探索;结论探索型是先探索结论再去证明,在探索过程中常先从特殊情况入手,通过观察、分析、归纳,进行猜测,得出结论,再就一般情况去论证结论.探究一探究二探究三思维辨析变式训练2如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱CC1,C1D1,D1D,CD的中点,N是BC的中点,点M在四边形EFGH的边及其内部运动,当点M在 时,有MN∥平面B1BDD1.?探究一探究二探究三思维辨析解析:点M在F,H的连线上时,有MN∥平面B1BDD1.如图,平面BDD1B1是正方体ABCD-A1B1C1D1的对角面,探究过点N且与平面BDD1B1平行的直线,可取B1C1的中点N1,连接N1N,则NN1∥平面BDD1B1,连接NH,则NH∥平面BDD1B1.
∵NH∩NN1=N,∴平面NN1FH∥平面BDD1B1.
∵MN?平面NN1FH,∴MN∥平面B1BDD1.
即点M在点F,H的连线上时,有MN∥平面B1BDD1.
答案:点F,H的连线上探究一探究二探究三思维辨析一题多解——证明直线与平面平行
典例如图,四边形ABCD和ADEF都是正方形,点M在BD上,N在AE上且BM=AN.求证:MN∥平面CDE.思路分析:由直线与平面平行的判定可知,本题的关键是在平面CDE中找到一条直线和MN平行.探究一探究二探究三思维辨析证明方法一 过M点作AD的平行线交CD于O,
过N作AD平行线交DE于P,连接OP.
显然OP在平面CDE上,且MO∥NP,
由于BM=AN,且正方形ABCD、ADEF共边,
∴MD=NE.
∴MO=NP,因此四边形MOPN为平行四边形,有MN∥OP,故MN∥平面CDE.探究一探究二探究三思维辨析方法二 连接AM并延长交CD于P.
又MN?平面CDE,EP?平面CDE,∴MN∥平面CDE.探究一探究二探究三思维辨析方法三 作MO⊥AB于点O,NP⊥AD于点P,连接PM,
∵四边形ABCD和四边形ADEF都是正方形,
∴∠BAD=∠ADE=90°,
∴OM∥AP,PN∥DE.
∵∠OBM=∠PAN=45°,
∵BM=AN,∴OM=AP.
∴四边形OMPA是平行四边形.
∴MP∥OA∥CD.
∵MP?平面PMN,PN?平面PMN,MP∩PN=P,
CD?平面CED,DE?平面CED,CD∩DE=D,
∴平面PMN∥平面CED.
∵MN?平面PMN,∴MN∥平面CED.探究一探究二探究三思维辨析方法总结 本题主要考查线面平行,解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,结合有关定理进行证明.方法一、二利用的是直线与平面平行的判定定理,方法三应用的是面面平行的性质定理.12341.下列图形中能正确表示语句“平面α∩β=l,a?α,b?β,a∥β”的是( )
解析:A中不能正确表达b?β;B中不能正确表达a∥β;C中也不能正确表达a∥β.D正确.
答案:D12342.平面α与△ABC的两边AB,AC分别交于点D,E,且AD∶DB=AE∶EC,如图所示,则BC与α的位置关系是( )
A.平行 B.相交
C.异面 D.BC?α
解析:在△ABC中,∵AD∶DB=AE∶EC,
∴BC∥DE.∵BC?α,DE?α,∴BC∥α.
答案:A12343.两个平面平行的条件是( )
A.一个平面内一条直线平行于另一个平面
B.一个平面内两条直线平行于另一个平面
C.一个平面内的任意一条直线平行于另一个平面
D.两个平面都平行于同一条直线
解析:在选项A、选项B和选项D的条件下两个平面可能相交.
答案:C12344.如图,在长方体ABCD-A1B1C1D1中,与BC平行的平面是 ;与BC1平行的平面是 ;与平面A1B1C1D1和平面A1B1BA都平行的棱是 .?
解析:观察图形,根据直线与平面平行的判定定理可知,与BC平行的平面是平面A1B1C1D1与平面ADD1A1;与BC1平行的平面是平面ADD1A1;因为平面A1B1C1D1与平面A1B1BA的交线是A1B1,所以与其都平行的棱是DC.
答案:平面A1B1C1D1与平面ADD1A1 平面ADD1A1 DC
1.如图,将课本ABCD的一边AB紧贴桌面α,把课本绕AB转动,在转动过程中,AB的对边CD(不落在α内)和平面α有何位置关系?
提示:因为没有公共点,所以CD∥α. 一二2.填表:直线与平面平行的判定定理 3.做一做:能保证直线a与平面α平行的条件是( )
A.b?α,a∥b
B.b?α,c∥α,a∥b,a∥c
C.b?α,A,B∈a,C,D∈b,且AC∥BD
D.a?α,b?α,a∥b
答案:D一二二、平面与平面平行的判定定理
1.三角板的一条边所在直线与平面α平行,这个三角板所在平面与α平行吗?
提示:不一定平行.
2.三角板的两条边所在直线分别与平面α平行,这个三角板所在平面与α平行吗?
提示:平行.
3.如图,平面BCC1B1内有多少条直线与平面ABCD平行?这两个平面平行吗?
提示:无数条,不平行.一二4.填表:平面与平面平行的判定定理 5.做一做:若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )
A.平行 B.相交 C.平行或相交 D.以上都不对
答案:C一二6.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)如果一条直线和一个平面内的另一条直线平行,那么这条直线和这个平面平行. ( )
(2)如果一个平面内有两条直线和另一个平面平行,那么这两个平面平行. ( )
(3)如果一个平面内有无数条直线和另一个平面平行,那么这两个平面平行. ( )
答案:(1)× (2)× (3)×探究一探究二探究三思维辨析直线与平面平行的判定
例1如图,在正方体ABCD-A1B1C1D1中,E,F,G分别是BC,CC1,BB1的中点,求证:EF∥平面AD1G.思路分析:根据直线与平面平行的判定定理进行证明即可. 探究一探究二探究三思维辨析证明连接BC1,则由E,F分别是BC,CC1的中点知,EF∥BC1.
又AB??A1B1??D1C1,
所以四边形ABC1D1是平行四边形,
所以BC1∥AD1,所以EF∥AD1.
又EF?平面AD1G,AD1?平面AD1G,
所以EF∥平面AD1G.探究一探究二探究三思维辨析反思感悟证明直线与平面平行的思路及步骤
(1)证明直线与平面平行,可以用定义,也可以用判定定理,但说明直线与平面没有公共点不是很容易(当然也可用反证法),所以更多的是用判定定理.(2)用判定定理证明直线与平面平行的步骤如下:探究一探究二探究三思维辨析变式训练1如图,P是?ABCD所在平面外一点,E,F分别为AB,PD的中点,求证:AF∥平面PEC.
证明:设PC的中点为G,连接EG,FG.
∵F为PD的中点,∴GF∥CD,且GF= CD.
∵AB∥CD,AB=CD,E为AB的中点,
∴GF∥AE,GF=AE,
∴四边形AEGF为平行四边形,
∴EG∥AF.
又∵AF?平面PEC,EG?平面PEC,∴AF∥平面PEC.探究一探究二探究三思维辨析平面与平面平行的判定
例2如图所示,在正方体ABCD-A1B1C1D1中,M,E,F,N分别是A1B1,B1C1,C1D1,D1A1的中点,求证:
(1)E,F,B,D四点共面;
(2)平面MAN∥平面EFDB.
思路分析:(1)只需证明BD∥EF,即可证明E,F,B,D共面.(2)要证平面MAN∥平面EFDB,只需证MN∥平面EFDB,AM∥平面EFDB.探究一探究二探究三思维辨析证明:(1)连接B1D1.
∵E,F分别是B1C1和C1D1的中点,
∴EF∥B1D1.而BD∥B1D1,
∴BD∥EF.∴E,F,B,D四点共面.
(2)由题意知MN∥B1D1,B1D1∥BD,
∴MN∥BD.
而MN?平面EFDB,
∴MN∥平面EFDB,连接MF.
∵点M,F分别是A1B1与C1D1的中点,∴MF??AD.
∴四边形ADFM是平行四边形.∴AM∥DF.
∵AM?平面EFDB,DF?平面EFDB,∴AM∥平面EFDB.又AM∩MN=M,∴平面MAN∥平面EFDB.探究一探究二探究三思维辨析反思感悟证明平面与平面平行的思路及步骤
(1)证明两个平面平行,可以用定义,也可以用判定定理.但用定义证明时,需说明两个平面没有公共点,这一点也不容易做到(可用反证法).
(2)用判定定理证明两个平面平行,其步骤如下:探究一探究二探究三思维辨析延伸探究本例中,设P是棱AA1的中点,其他条件不变,求证:平面PMN∥平面C1BD.
证明:连接AB1.
∵P,M分别是AA1,A1B1的中点,∴PM∥AB1.
又AB1∥C1D,∴PM∥C1D.
又PM?平面C1BD,C1D?平面C1BD,∴PM∥平面C1BD.
同理MN∥平面C1BD.又PM∩MN=M,
∴平面PMN∥平面C1BD.探究一探究二探究三思维辨析线面平行、面面平行判定定理的综合
例3如图,四边形ABCD是平行四边形,点E,F,G分别为线段BC,PB,AD的中点.
(1)求证:EF∥平面PAC;
(2)求证:平面PCG∥平面AEF;
(3)在线段BD上找一点H,使得FH∥平面PCG,并说明理由.探究一探究二探究三思维辨析(1)证明∵E,F分别是BC,BP中点,
∵PC?平面PAC,EF?平面PAC,
∴EF∥平面PAC.
(2)证明∵E,G分别是BC,AD中点,
∴AE∥CG,
∵AE?平面PCG,CG?平面PCG,
∴AE∥平面PCG,
又∵EF∥PC,
PC?平面PCG,EF?平面PCG,
∴EF∥平面PCG,
AE∩EF=E,AE,EF?平面AEF,
∴平面AEF∥平面PCG.探究一探究二探究三思维辨析(3)解设AE,GC与BD分别交于M,N两点,
由(2)知,平面PCG∥平面AEF.
∵点F,M在平面AEF上,连接点F,点M,
则FM?平面AEF,且FM?平面PCG.
∴FM∥平面PCG,
即M点为所找的H点.
反思感悟探索型问题的常见类型
常见的有以下两类:条件探索型和结论探索型.条件探索型问题是针对一个结论,条件未知需探索;结论探索型是先探索结论再去证明,在探索过程中常先从特殊情况入手,通过观察、分析、归纳,进行猜测,得出结论,再就一般情况去论证结论.探究一探究二探究三思维辨析变式训练2如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱CC1,C1D1,D1D,CD的中点,N是BC的中点,点M在四边形EFGH的边及其内部运动,当点M在 时,有MN∥平面B1BDD1.?探究一探究二探究三思维辨析解析:点M在F,H的连线上时,有MN∥平面B1BDD1.如图,平面BDD1B1是正方体ABCD-A1B1C1D1的对角面,探究过点N且与平面BDD1B1平行的直线,可取B1C1的中点N1,连接N1N,则NN1∥平面BDD1B1,连接NH,则NH∥平面BDD1B1.
∵NH∩NN1=N,∴平面NN1FH∥平面BDD1B1.
∵MN?平面NN1FH,∴MN∥平面B1BDD1.
即点M在点F,H的连线上时,有MN∥平面B1BDD1.
答案:点F,H的连线上探究一探究二探究三思维辨析一题多解——证明直线与平面平行
典例如图,四边形ABCD和ADEF都是正方形,点M在BD上,N在AE上且BM=AN.求证:MN∥平面CDE.思路分析:由直线与平面平行的判定可知,本题的关键是在平面CDE中找到一条直线和MN平行.探究一探究二探究三思维辨析证明方法一 过M点作AD的平行线交CD于O,
过N作AD平行线交DE于P,连接OP.
显然OP在平面CDE上,且MO∥NP,
由于BM=AN,且正方形ABCD、ADEF共边,
∴MD=NE.
∴MO=NP,因此四边形MOPN为平行四边形,有MN∥OP,故MN∥平面CDE.探究一探究二探究三思维辨析方法二 连接AM并延长交CD于P.
又MN?平面CDE,EP?平面CDE,∴MN∥平面CDE.探究一探究二探究三思维辨析方法三 作MO⊥AB于点O,NP⊥AD于点P,连接PM,
∵四边形ABCD和四边形ADEF都是正方形,
∴∠BAD=∠ADE=90°,
∴OM∥AP,PN∥DE.
∵∠OBM=∠PAN=45°,
∵BM=AN,∴OM=AP.
∴四边形OMPA是平行四边形.
∴MP∥OA∥CD.
∵MP?平面PMN,PN?平面PMN,MP∩PN=P,
CD?平面CED,DE?平面CED,CD∩DE=D,
∴平面PMN∥平面CED.
∵MN?平面PMN,∴MN∥平面CED.探究一探究二探究三思维辨析方法总结 本题主要考查线面平行,解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,结合有关定理进行证明.方法一、二利用的是直线与平面平行的判定定理,方法三应用的是面面平行的性质定理.12341.下列图形中能正确表示语句“平面α∩β=l,a?α,b?β,a∥β”的是( )
解析:A中不能正确表达b?β;B中不能正确表达a∥β;C中也不能正确表达a∥β.D正确.
答案:D12342.平面α与△ABC的两边AB,AC分别交于点D,E,且AD∶DB=AE∶EC,如图所示,则BC与α的位置关系是( )
A.平行 B.相交
C.异面 D.BC?α
解析:在△ABC中,∵AD∶DB=AE∶EC,
∴BC∥DE.∵BC?α,DE?α,∴BC∥α.
答案:A12343.两个平面平行的条件是( )
A.一个平面内一条直线平行于另一个平面
B.一个平面内两条直线平行于另一个平面
C.一个平面内的任意一条直线平行于另一个平面
D.两个平面都平行于同一条直线
解析:在选项A、选项B和选项D的条件下两个平面可能相交.
答案:C12344.如图,在长方体ABCD-A1B1C1D1中,与BC平行的平面是 ;与BC1平行的平面是 ;与平面A1B1C1D1和平面A1B1BA都平行的棱是 .?
解析:观察图形,根据直线与平面平行的判定定理可知,与BC平行的平面是平面A1B1C1D1与平面ADD1A1;与BC1平行的平面是平面ADD1A1;因为平面A1B1C1D1与平面A1B1BA的交线是A1B1,所以与其都平行的棱是DC.
答案:平面A1B1C1D1与平面ADD1A1 平面ADD1A1 DC
