2.3.1直线与平面垂直的判定课件(31张)
文档属性
| 名称 | 2.3.1直线与平面垂直的判定课件(31张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 13:34:59 | ||
图片预览







文档简介
课件31张PPT。2.3 直线、平面垂直的判定及其性质2.3.1 直线与平面垂直的判定一二三一、直线与平面垂直的定义
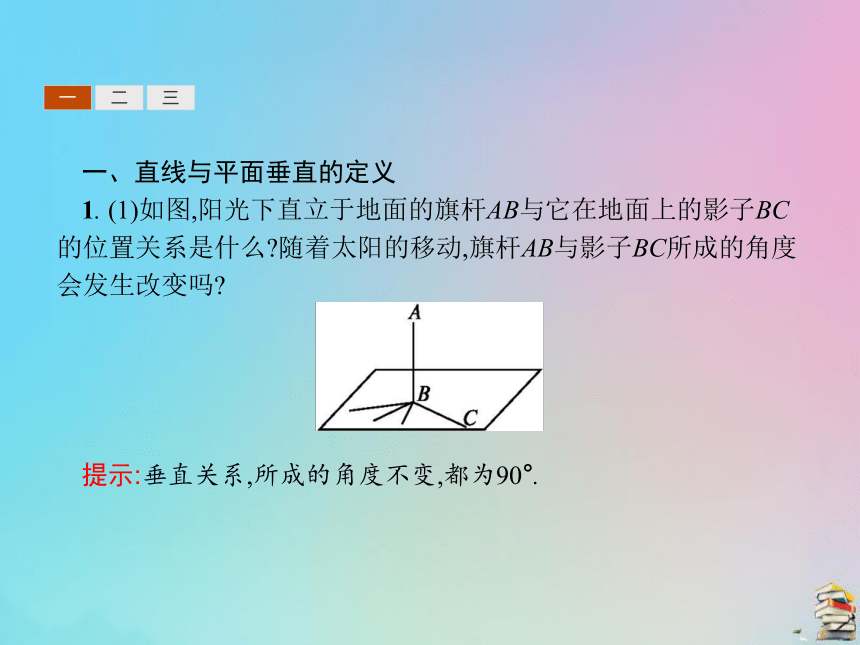
1. (1)如图,阳光下直立于地面的旗杆AB与它在地面上的影子BC的位置关系是什么?随着太阳的移动,旗杆AB与影子BC所成的角度会发生改变吗?
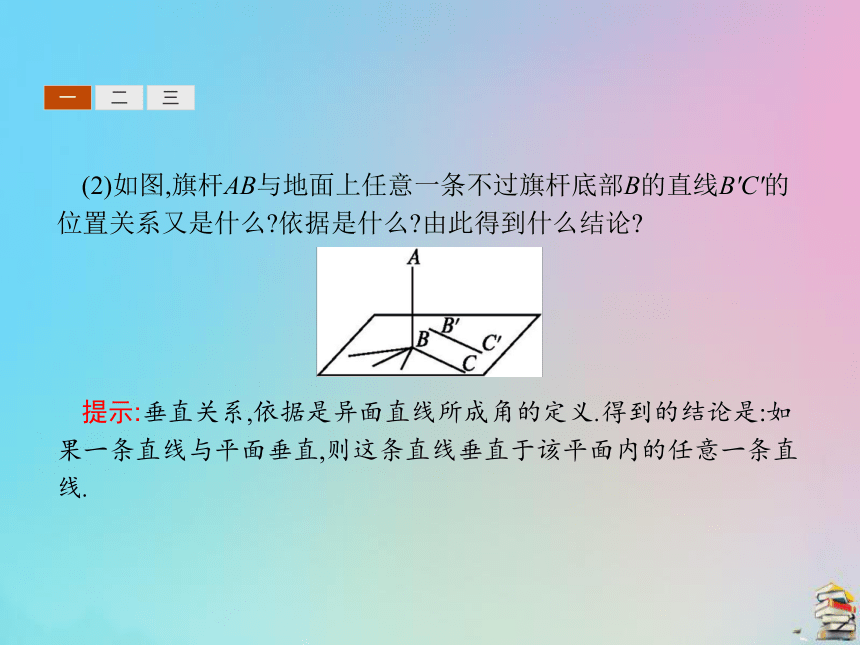
提示:垂直关系,所成的角度不变,都为90°.一二三(2)如图,旗杆AB与地面上任意一条不过旗杆底部B的直线B'C'的位置关系又是什么?依据是什么?由此得到什么结论?
提示:垂直关系,依据是异面直线所成角的定义.得到的结论是:如果一条直线与平面垂直,则这条直线垂直于该平面内的任意一条直线.一二三2.填表:直线与平面垂直的定义 一二三二、直线与平面垂直的判定定理
1.如图,直线l与平面α内的无数条直线a,b,c…都垂直,直线l与平面α一定垂直吗?为什么?
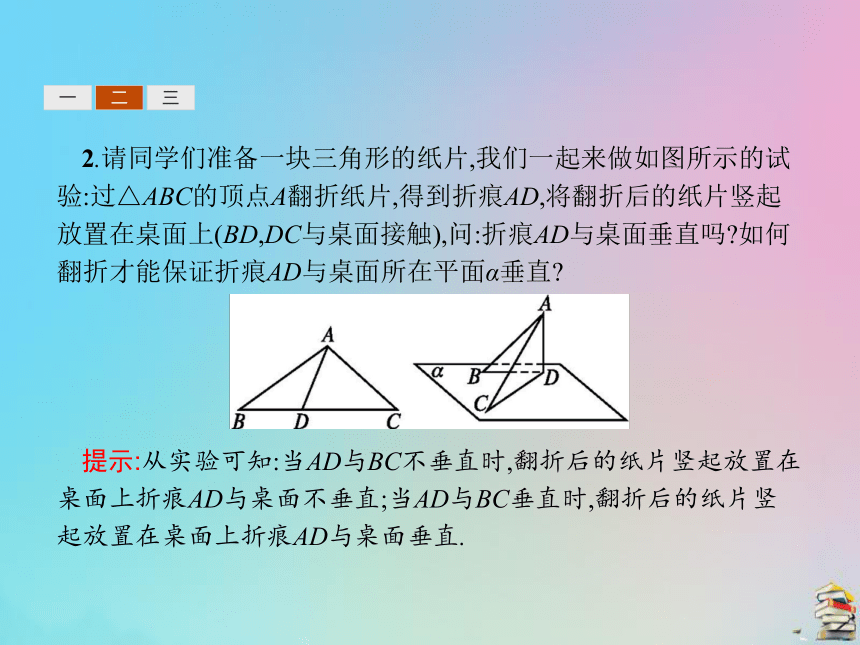
提示:不一定.当平面α内的无数条直线a,b,c…都互相平行时,直线l在保证与直线a,b,c…都垂直的条件下,与平面α可能垂直也可能斜交.一二三2.请同学们准备一块三角形的纸片,我们一起来做如图所示的试验:过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触),问:折痕AD与桌面垂直吗?如何翻折才能保证折痕AD与桌面所在平面α垂直?
提示:从实验可知:当AD与BC不垂直时,翻折后的纸片竖起放置在桌面上折痕AD与桌面不垂直;当AD与BC垂直时,翻折后的纸片竖起放置在桌面上折痕AD与桌面垂直.一二三3.由折痕AD⊥BC,翻折之后垂直关系不变,即AD⊥CD,AD⊥BD.由此你能得到什么结论?
提示:若一条直线与平面内两条相交直线垂直且相交,则该直线垂直这个平面.
4.填表:直线和平面垂直的判定定理一二三5.做一做:
下列说法中正确的个数是( )
①如果直线l与平面α内的两条相交直线都垂直,则l⊥α;②如果直线l与平面α内的任意一条直线垂直,则l⊥α;③如果直线l不垂直于α,则α内没有与l垂直的直线;④如果直线l不垂直于α,则α内也可以有无数条直线与l垂直.
A.0 B.1
C.2 D.3
解析:由直线和平面垂直的判定定理知①正确;由直线与平面垂直的定义知,②正确;当直线l与平面α不垂直时,l可能与α内的无数条直线垂直,故③不对;④正确.
答案:D一二三三、直线与平面所成的角
1.平面的斜线、斜足是怎样定义的?斜线在平面上的射影是如何定义的?什么是斜线与平面所成的角?
提示:如图,一条直线PA和一个平面α相交,但不和平面α垂直,这条直线PA叫做这个平面α的斜线,它们的交点A叫做斜足.过斜线PA上斜足A以外的一点P向平面α引垂线PO,过垂足O和斜足A的直线AO叫做斜线PA在平面α上的射影.斜线PA和它在平面α上的射影AO所成的锐角∠PAO,叫做斜线PA和平面α所成的角.一二三2.直线与平面所成的角θ的取值范围是什么?
提示:一条直线垂直于平面,我们说它们所成的角等于90°;一条直线和平面平行,或在平面内,我们说它们所成的角等于0°.因此,直线与平面所成的角α的范围是0°≤α≤90°.一二三3.做一做:如图,在正方体ABCD-A1B1C1D1中,直线AB1与平面ABCD所成的角等于 ;AB1与平面ADD1A1所成的角等于 ;AB1与平面DCC1D1所成的角等于 .?
解析:∠B1AB为AB1与平面ABCD所成的角即45°;∠B1AA1为AB1与平面ADD1A1所成的角,即45°;AB1与平面DCC1D1平行,即所成的角为0°.
答案:45° 45° 0°探究一探究二探究三思想方法证明直线与平面垂直
例1如图所示,在△ABC中,∠ABC=90°,D是AC的中点,S是△ABC所在平面外一点,且SA=SB=SC.
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
思路分析:题设条件中的三棱锥的三条侧棱相等,AB⊥BC,D是AC的中点,要证(1),需在平面ABC内找两条相交直线与SD垂直,故等腰三角形底边的中线是可以利用的垂直关系,要证(2),需设法在平面SAC内找两条相交直线与BD垂直,而(1)的结论可利用.探究一探究二探究三思想方法证明(1)∵SA=SC,D为AC的中点,∴SD⊥AC.
连接BD.
在Rt△ABC中,有AD=DC=DB,
∴△SDB≌△SDA.
∴∠SDB=∠SDA=90°.
∴SD⊥BD.
又AC∩BD=D,∴SD⊥平面ABC.
(2)∵AB=BC,D是AC的中点,∴BD⊥AC.
又由(1)知SD⊥BD,且AC∩SD=D,
∴BD⊥平面SAC.探究一探究二探究三思想方法方法总结 证线面垂直的方法
1.线线垂直证明线面垂直
(1)定义法(不常用);
(2)判定定理最常用(有时作辅助线).
2.平行转化法(利用推论)
(1)a∥b,a⊥α?b⊥α;
(2)α∥β,a⊥α?a⊥β.探究一探究二探究三思想方法变式训练 如图所示,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.
求证:AD⊥平面A1DC1.
证明∵AA1⊥底面ABC,平面A1B1C1∥平面ABC,
∴AA1⊥平面A1B1C1,
∴A1C1⊥AA1.又∠B1A1C1=90°,
∴A1C1⊥A1B1.而A1B1∩AA1=A1,
∴A1C1⊥平面AA1B1B.又AD?平面AA1B1B,
∴A1C1⊥AD.
∴A1D⊥AD.∵A1C1∩A1D=A1,
∴AD⊥平面A1DC1.探究一探究二探究三思想方法证明两直线垂直
例2 如图,已知PA垂直于☉O所在的平面,AB是☉O的直径,C是☉O上任意一点,求证:BC⊥PC.
思路分析:首先利用PA⊥平面ABC得到PA⊥BC,然后根据圆的性质得到AC⊥BC,进而利用线面垂直判定定理证得BC⊥平面PAC,从而得到BC⊥PC.
证明:∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC.
∵AB是☉O的直径,∴BC⊥AC.
而PA∩AC=A,∴BC⊥平面PAC.
∵PC?平面PAC,∴BC⊥PC.探究一探究二探究三思想方法反思感悟线线垂直的证明方法
要证明两条直线垂直(无论它们是异面还是共面),通常是证明其中的一条直线垂直于另一条直线所在的一个平面.探究一探究二探究三思想方法延伸探究若本例中其他条件不变,作AE⊥PC交PC于点E,求证:AE⊥PB.
证明:由【例2】知BC⊥平面PAC,
∵AE?平面PAC,∴BC⊥AE.
∵PC⊥AE,且PC∩BC=C,
∴AE⊥平面PBC.
∵PB?平面PBC,∴AE⊥PB.探究一探究二探究三思想方法求直线与平面所成的角
例3已知四面体ABCD的棱长都相等,Q是AD的中点,则CQ与平面BCD所成的角的正弦值为 .?
思路分析:作AO⊥平面BCD,垂足为O,连接OD→取OD中点P,连接QP,CP→∠QCP就是斜线CQ与平面BCD所成的角→求出sin∠QCP探究一探究二探究三思想方法解析:过点A作AO⊥平面BCD,垂足为O,连接OB,OC,OD.
取OD中点P,连接QP,CP.
由AO⊥平面BCD,四面体的棱长都相等知点O是三角形三边垂直平分线的交点,也是三角形角平分线的交点.∵Q是AD中点,P是OD中点,∴QP∥AO.
∵AO⊥平面BCD,∴QP⊥平面BCD.
∴∠QCP就是CQ与平面BCD所成的角.
在正三角形ACD中,Q是AD的中点,探究一探究二探究三思想方法反思感悟求斜线与平面所成的角的步骤
(1)作图.作(或找)出斜线在平面上的射影,将空间角(斜线与平面所成的角)转化为平面角(两条相交直线所成的锐角).
(2)证明.证明找出的平面角是斜线与平面所成的角.
(3)计算.通常在垂线段、斜线和射影所组成的直角三角形中计算.探究一探究二探究三思想方法变式训练如图,在Rt△BMC中,斜边BM=5,它在平面ABC上的射影AB长为4,∠MBC=60°,则MC与平面CAB所成角的正弦值为 .?
解析:由题意知,点A是点M在平面ABC内的射影,
∴MA⊥平面ABC,
∴MC在平面CAB内的射影为AC.
∴∠MCA即为直线MC与平面CAB所成的角.
∵在Rt△MBC中,BM=5,∠MBC=60°,探究一探究二探究三思想方法数学思想——空间平行与垂直关系相互转化的综合应用
典例如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA∥平面EDB;
(2)求证:PB⊥平面EFD.探究一探究二探究三思想方法证明(1)连接AC交BD于点O.连接EO,如图.
∵底面ABCD是正方形,
∴点O是AC的中点.
在△PAC中EO是中位线,
∴PA∥EO.
而EO?平面EDB,且PA?平面EDB.
所以PA∥平面EDB.探究一探究二探究三思想方法(2)∵PD⊥底面ABCD,且DC?底面ABCD,
∴PD⊥DC.
∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,
∴DE⊥PC.①
同样由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,
∴BC⊥平面PDC.而DE?平面PDC,
∴BC⊥DE.②
由①和②推得DE⊥平面PBC.
而PB?平面PBC,∴DE⊥PB.
又EF⊥PB,且DE∩EF=E,∴PB⊥平面EFD.
方法总结 利用空间平行关系及垂直关系的判定定理进行证明,证明时一定要将定理的条件考虑全面,保证条件的齐全性.12341.若三条直线OA,OB,OC两两垂直,则直线OA垂直于 ( )
A.平面OAB B.平面OAC
C.平面OBC D.平面ABC
解析:∵OA⊥OB,OA⊥OC且OB∩OC=O,
∴OA⊥平面OBC.
答案:C12342.已知直线a⊥平面α,直线b∥平面α,则a与b的关系为 ( )
A.a∥b B.a⊥b
C.a,b相交不垂直 D.a,b异面不垂直
解析:由b∥α,过b作平面β,使α∩β=c,则b∥c,且c?α.∵a⊥α,∴a⊥c.∴a⊥b.
答案:B12343.在正方体A1B1C1D1-ABCD中,E,F分别是棱AB,BC的中点,O是底面ABCD的中心(如图),则EF与平面BB1O的关系是 .?
解析:由正方体性质知AC⊥BD,BB1⊥AC,
∵E,F是棱AB,BC的中点,
∴EF∥AC,
∴EF⊥BD,EF⊥BB1,
∴EF⊥平面BB1O.
答案:垂直12344.若斜线段AB是它在平面α上的射影长的2倍,则AB与平面α所成的角是( )
A.60° B.45° C.30° D.120°
解析:斜线段、垂线段以及射影构成直角三角形.如图所示,∠ABO即是斜线AB与平面α所成的角,又AB=2BO,所以cos
所以∠ABO=60°.
答案:A
1. (1)如图,阳光下直立于地面的旗杆AB与它在地面上的影子BC的位置关系是什么?随着太阳的移动,旗杆AB与影子BC所成的角度会发生改变吗?
提示:垂直关系,所成的角度不变,都为90°.一二三(2)如图,旗杆AB与地面上任意一条不过旗杆底部B的直线B'C'的位置关系又是什么?依据是什么?由此得到什么结论?
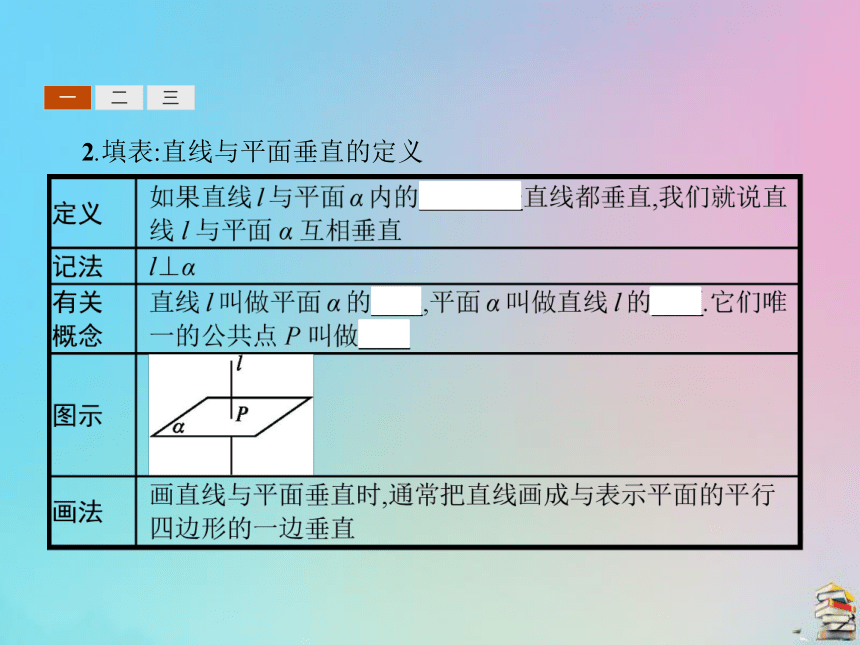
提示:垂直关系,依据是异面直线所成角的定义.得到的结论是:如果一条直线与平面垂直,则这条直线垂直于该平面内的任意一条直线.一二三2.填表:直线与平面垂直的定义 一二三二、直线与平面垂直的判定定理
1.如图,直线l与平面α内的无数条直线a,b,c…都垂直,直线l与平面α一定垂直吗?为什么?
提示:不一定.当平面α内的无数条直线a,b,c…都互相平行时,直线l在保证与直线a,b,c…都垂直的条件下,与平面α可能垂直也可能斜交.一二三2.请同学们准备一块三角形的纸片,我们一起来做如图所示的试验:过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触),问:折痕AD与桌面垂直吗?如何翻折才能保证折痕AD与桌面所在平面α垂直?
提示:从实验可知:当AD与BC不垂直时,翻折后的纸片竖起放置在桌面上折痕AD与桌面不垂直;当AD与BC垂直时,翻折后的纸片竖起放置在桌面上折痕AD与桌面垂直.一二三3.由折痕AD⊥BC,翻折之后垂直关系不变,即AD⊥CD,AD⊥BD.由此你能得到什么结论?
提示:若一条直线与平面内两条相交直线垂直且相交,则该直线垂直这个平面.
4.填表:直线和平面垂直的判定定理一二三5.做一做:
下列说法中正确的个数是( )
①如果直线l与平面α内的两条相交直线都垂直,则l⊥α;②如果直线l与平面α内的任意一条直线垂直,则l⊥α;③如果直线l不垂直于α,则α内没有与l垂直的直线;④如果直线l不垂直于α,则α内也可以有无数条直线与l垂直.
A.0 B.1
C.2 D.3
解析:由直线和平面垂直的判定定理知①正确;由直线与平面垂直的定义知,②正确;当直线l与平面α不垂直时,l可能与α内的无数条直线垂直,故③不对;④正确.
答案:D一二三三、直线与平面所成的角
1.平面的斜线、斜足是怎样定义的?斜线在平面上的射影是如何定义的?什么是斜线与平面所成的角?
提示:如图,一条直线PA和一个平面α相交,但不和平面α垂直,这条直线PA叫做这个平面α的斜线,它们的交点A叫做斜足.过斜线PA上斜足A以外的一点P向平面α引垂线PO,过垂足O和斜足A的直线AO叫做斜线PA在平面α上的射影.斜线PA和它在平面α上的射影AO所成的锐角∠PAO,叫做斜线PA和平面α所成的角.一二三2.直线与平面所成的角θ的取值范围是什么?
提示:一条直线垂直于平面,我们说它们所成的角等于90°;一条直线和平面平行,或在平面内,我们说它们所成的角等于0°.因此,直线与平面所成的角α的范围是0°≤α≤90°.一二三3.做一做:如图,在正方体ABCD-A1B1C1D1中,直线AB1与平面ABCD所成的角等于 ;AB1与平面ADD1A1所成的角等于 ;AB1与平面DCC1D1所成的角等于 .?
解析:∠B1AB为AB1与平面ABCD所成的角即45°;∠B1AA1为AB1与平面ADD1A1所成的角,即45°;AB1与平面DCC1D1平行,即所成的角为0°.
答案:45° 45° 0°探究一探究二探究三思想方法证明直线与平面垂直
例1如图所示,在△ABC中,∠ABC=90°,D是AC的中点,S是△ABC所在平面外一点,且SA=SB=SC.
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
思路分析:题设条件中的三棱锥的三条侧棱相等,AB⊥BC,D是AC的中点,要证(1),需在平面ABC内找两条相交直线与SD垂直,故等腰三角形底边的中线是可以利用的垂直关系,要证(2),需设法在平面SAC内找两条相交直线与BD垂直,而(1)的结论可利用.探究一探究二探究三思想方法证明(1)∵SA=SC,D为AC的中点,∴SD⊥AC.
连接BD.
在Rt△ABC中,有AD=DC=DB,
∴△SDB≌△SDA.
∴∠SDB=∠SDA=90°.
∴SD⊥BD.
又AC∩BD=D,∴SD⊥平面ABC.
(2)∵AB=BC,D是AC的中点,∴BD⊥AC.
又由(1)知SD⊥BD,且AC∩SD=D,
∴BD⊥平面SAC.探究一探究二探究三思想方法方法总结 证线面垂直的方法
1.线线垂直证明线面垂直
(1)定义法(不常用);
(2)判定定理最常用(有时作辅助线).
2.平行转化法(利用推论)
(1)a∥b,a⊥α?b⊥α;
(2)α∥β,a⊥α?a⊥β.探究一探究二探究三思想方法变式训练 如图所示,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.
求证:AD⊥平面A1DC1.
证明∵AA1⊥底面ABC,平面A1B1C1∥平面ABC,
∴AA1⊥平面A1B1C1,
∴A1C1⊥AA1.又∠B1A1C1=90°,
∴A1C1⊥A1B1.而A1B1∩AA1=A1,
∴A1C1⊥平面AA1B1B.又AD?平面AA1B1B,
∴A1C1⊥AD.
∴A1D⊥AD.∵A1C1∩A1D=A1,
∴AD⊥平面A1DC1.探究一探究二探究三思想方法证明两直线垂直
例2 如图,已知PA垂直于☉O所在的平面,AB是☉O的直径,C是☉O上任意一点,求证:BC⊥PC.
思路分析:首先利用PA⊥平面ABC得到PA⊥BC,然后根据圆的性质得到AC⊥BC,进而利用线面垂直判定定理证得BC⊥平面PAC,从而得到BC⊥PC.
证明:∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC.
∵AB是☉O的直径,∴BC⊥AC.
而PA∩AC=A,∴BC⊥平面PAC.
∵PC?平面PAC,∴BC⊥PC.探究一探究二探究三思想方法反思感悟线线垂直的证明方法
要证明两条直线垂直(无论它们是异面还是共面),通常是证明其中的一条直线垂直于另一条直线所在的一个平面.探究一探究二探究三思想方法延伸探究若本例中其他条件不变,作AE⊥PC交PC于点E,求证:AE⊥PB.
证明:由【例2】知BC⊥平面PAC,
∵AE?平面PAC,∴BC⊥AE.
∵PC⊥AE,且PC∩BC=C,
∴AE⊥平面PBC.
∵PB?平面PBC,∴AE⊥PB.探究一探究二探究三思想方法求直线与平面所成的角
例3已知四面体ABCD的棱长都相等,Q是AD的中点,则CQ与平面BCD所成的角的正弦值为 .?
思路分析:作AO⊥平面BCD,垂足为O,连接OD→取OD中点P,连接QP,CP→∠QCP就是斜线CQ与平面BCD所成的角→求出sin∠QCP探究一探究二探究三思想方法解析:过点A作AO⊥平面BCD,垂足为O,连接OB,OC,OD.
取OD中点P,连接QP,CP.
由AO⊥平面BCD,四面体的棱长都相等知点O是三角形三边垂直平分线的交点,也是三角形角平分线的交点.∵Q是AD中点,P是OD中点,∴QP∥AO.
∵AO⊥平面BCD,∴QP⊥平面BCD.
∴∠QCP就是CQ与平面BCD所成的角.
在正三角形ACD中,Q是AD的中点,探究一探究二探究三思想方法反思感悟求斜线与平面所成的角的步骤
(1)作图.作(或找)出斜线在平面上的射影,将空间角(斜线与平面所成的角)转化为平面角(两条相交直线所成的锐角).
(2)证明.证明找出的平面角是斜线与平面所成的角.
(3)计算.通常在垂线段、斜线和射影所组成的直角三角形中计算.探究一探究二探究三思想方法变式训练如图,在Rt△BMC中,斜边BM=5,它在平面ABC上的射影AB长为4,∠MBC=60°,则MC与平面CAB所成角的正弦值为 .?
解析:由题意知,点A是点M在平面ABC内的射影,
∴MA⊥平面ABC,
∴MC在平面CAB内的射影为AC.
∴∠MCA即为直线MC与平面CAB所成的角.
∵在Rt△MBC中,BM=5,∠MBC=60°,探究一探究二探究三思想方法数学思想——空间平行与垂直关系相互转化的综合应用
典例如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA∥平面EDB;
(2)求证:PB⊥平面EFD.探究一探究二探究三思想方法证明(1)连接AC交BD于点O.连接EO,如图.
∵底面ABCD是正方形,
∴点O是AC的中点.
在△PAC中EO是中位线,
∴PA∥EO.
而EO?平面EDB,且PA?平面EDB.
所以PA∥平面EDB.探究一探究二探究三思想方法(2)∵PD⊥底面ABCD,且DC?底面ABCD,
∴PD⊥DC.
∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,
∴DE⊥PC.①
同样由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,
∴BC⊥平面PDC.而DE?平面PDC,
∴BC⊥DE.②
由①和②推得DE⊥平面PBC.
而PB?平面PBC,∴DE⊥PB.
又EF⊥PB,且DE∩EF=E,∴PB⊥平面EFD.
方法总结 利用空间平行关系及垂直关系的判定定理进行证明,证明时一定要将定理的条件考虑全面,保证条件的齐全性.12341.若三条直线OA,OB,OC两两垂直,则直线OA垂直于 ( )
A.平面OAB B.平面OAC
C.平面OBC D.平面ABC
解析:∵OA⊥OB,OA⊥OC且OB∩OC=O,
∴OA⊥平面OBC.
答案:C12342.已知直线a⊥平面α,直线b∥平面α,则a与b的关系为 ( )
A.a∥b B.a⊥b
C.a,b相交不垂直 D.a,b异面不垂直
解析:由b∥α,过b作平面β,使α∩β=c,则b∥c,且c?α.∵a⊥α,∴a⊥c.∴a⊥b.
答案:B12343.在正方体A1B1C1D1-ABCD中,E,F分别是棱AB,BC的中点,O是底面ABCD的中心(如图),则EF与平面BB1O的关系是 .?
解析:由正方体性质知AC⊥BD,BB1⊥AC,
∵E,F是棱AB,BC的中点,
∴EF∥AC,
∴EF⊥BD,EF⊥BB1,
∴EF⊥平面BB1O.
答案:垂直12344.若斜线段AB是它在平面α上的射影长的2倍,则AB与平面α所成的角是( )
A.60° B.45° C.30° D.120°
解析:斜线段、垂线段以及射影构成直角三角形.如图所示,∠ABO即是斜线AB与平面α所成的角,又AB=2BO,所以cos
所以∠ABO=60°.
答案:A
