2.3.3_2.3.4直线与平面垂直的性质平面与平面垂直的性质课件(21张)
文档属性
| 名称 | 2.3.3_2.3.4直线与平面垂直的性质平面与平面垂直的性质课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 914.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 13:35:31 | ||
图片预览







文档简介
课件21张PPT。2.3.3~2.3.4 直线与平面垂直的性质
平面与平面垂直的性质一二一、直线与平面垂直的性质定理
1.在日常生活中常见到一排排和地面垂直的电线杆.一排电线杆中的每根电线杆都与地面垂直,那么这些电线杆之间存在什么位置关系呢?
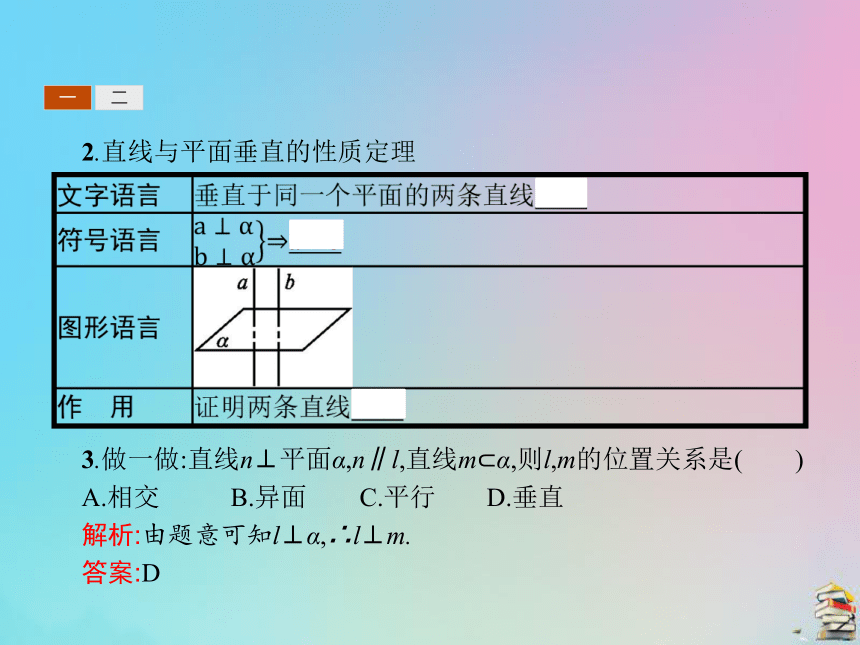
提示:平行.一二2.直线与平面垂直的性质定理 3.做一做:直线n⊥平面α,n∥l,直线m?α,则l,m的位置关系是( )
A.相交 B.异面 C.平行 D.垂直
解析:由题意可知l⊥α,∴l⊥m.
答案:D一二二、平面与平面垂直的性质定理
1.黑板所在平面与地面所在平面垂直,你能否在黑板上画一条直线与地面垂直?
提示:容易发现墙壁与墙壁所在平面的交线与地面垂直,因此只要在黑板上画出一条与这条交线平行的直线,则所画直线必与地面垂直.一二2.填表:平面与平面垂直的性质定理 一二3.做一做:若平面α⊥平面β,平面β⊥平面γ,则 ( )
A.α∥γ
B.α⊥γ
C.α与γ相交但不垂直
D.以上都有可能
答案:D探究一探究二思想方法直线与平面垂直的性质的应用
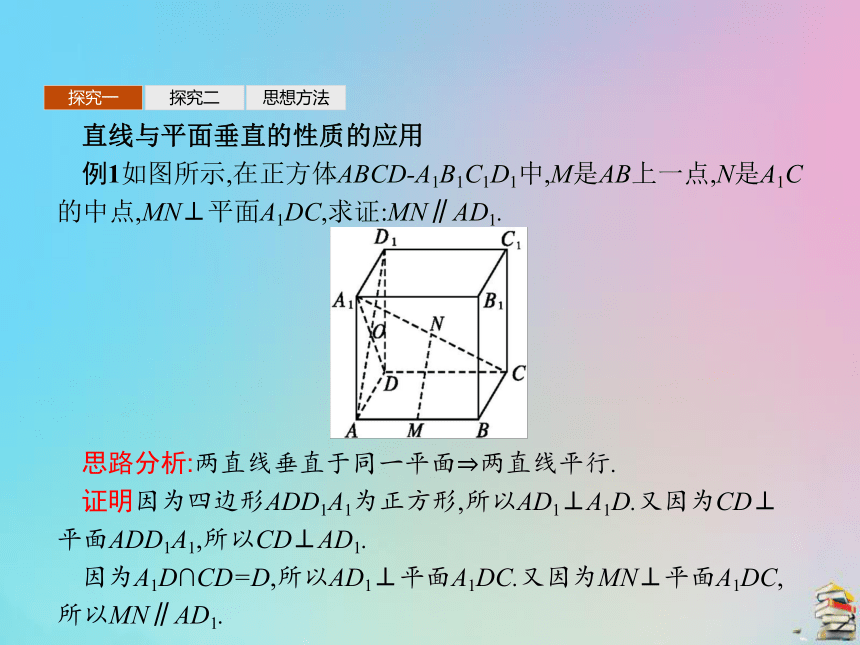
例1如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证:MN∥AD1.
思路分析:两直线垂直于同一平面?两直线平行.
证明因为四边形ADD1A1为正方形,所以AD1⊥A1D.又因为CD⊥平面ADD1A1,所以CD⊥AD1.
因为A1D∩CD=D,所以AD1⊥平面A1DC.又因为MN⊥平面A1DC,所以MN∥AD1.探究一探究二思想方法反思感悟1.线面垂直的性质:应用直线与平面垂直的常见性质达到证明线线平行的目的,即线面垂直的性质提供了证明线线平行的依据.
2.直线与平面垂直的其他性质:
(1)若一条直线垂直于一个平面,则它就垂直于这个平面内的任意一条直线;
(2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面;
(3)若一条直线垂直于两个平行平面中的一个,则它必垂直于另一个平面;
(4)垂直于同一条直线的两个平面平行.探究一探究二思想方法延伸探究1本例中条件不变,求证:M是AB中点.
证明连接ON,在△A1DC中,A1O=OD,A1N=NC.
所以ON∥AM.
又因为由例题可知MN∥OA,
所以四边形AMNO为平行四边形,
所以ON=AM.
所以M是AB的中点.探究一探究二思想方法延伸探究2本例中把条件“MN⊥平面A1DC”改为“M是AB中点”,求证:MN⊥平面A1DC.
证明连接A1M,CM,取CD中点P,连接NP,MP,
由正方体AC1,M,N为中点,则A1M=CM,
所以MN⊥A1C.
又P为CD中点,所以PN∥A1D.
因为CD⊥A1D,所以CD⊥PN.
又MP⊥CD,MP∩PN=P,
所以CD⊥平面MPN.
因为MN?平面MPN,
所以MN⊥CD.
又A1C∩CD=C,
所以MN⊥平面A1DC.探究一探究二思想方法平面与平面垂直的性质的应用
例2 如图,已知V是△ABC外一点,VA⊥平面ABC,平面VAB⊥平面VBC.求证:AB⊥BC.
思路分析:要证AB⊥BC,可证BC⊥平面VAB,易得VA⊥BC.又平面VAB⊥平面VBC,所以可在平面VAB内过A作VB的垂线,即与BC垂直,可得证.探究一探究二思想方法证明:在平面VAB内,过点A作AD⊥VB于点D.
∵平面VAB⊥平面VBC,且交线为VB,
∴AD⊥平面VBC.∴AD⊥BC.
∵VA⊥平面ABC,∴VA⊥BC.
∵AD∩VA=A,且VA?平面VAB,AD?平面VAB,
∴BC⊥平面VAB.
∵AB?平面VAB,
∴AB⊥BC.探究一探究二思想方法反思感悟面面垂直的常见性质
1.在运用面面垂直的性质定理时,若没有与交线垂直的直线,一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线,这样便把面面垂直问题转化为线面垂直问题,进而转化为线线垂直问题.
2.平面与平面垂直的其他性质:
(1)如果两个平面垂直,那么经过第一个平面内一点垂直于第二个平面的直线在第一个平面内.
(2)如果两个平面垂直,那么与其中一个平面平行的平面垂直于另一个平面.
(3)如果两个平面垂直,那么其中一个平面的垂线平行于另一个平面或在另一个平面内.探究一探究二思想方法延伸探究【例2】中的已知换为:平面VAB⊥平面ABC,平面VAC⊥平面ABC,CA⊥AB.试证:VA⊥BC.
证明:∵平面VAB⊥平面ABC,
平面VAB∩平面ABC=AB,AC?平面ABC,CA⊥AB,
∴CA⊥平面VAB,∴CA⊥VA.
同理,BA⊥VA.
又AB∩AC=A,∴VA⊥平面ABC,
∵BC?平面ABC,∴VA⊥BC.探究一探究二思想方法转化思想在线线、线面、面面垂直中的应用
典例 已知α,β,γ是三个不同的平面,l为直线,α⊥γ,β⊥γ,α∩β=l.求证:l⊥γ.
【审题视角】 根据直线和平面垂直的判定定理,可在γ内构造两相交直线分别与平面α,β垂直;或者由面面垂直的性质易在α,β内作出平面γ的垂线,再设法证明l与其平行即可.探究一探究二思想方法证法一在γ内取一点P,作PA垂直α与γ的交线于点A,PB垂直β与γ的交线于点B,则PA⊥α,PB⊥β.
∵l=α∩β,
∴l⊥PA,l⊥PB.
又PA∩PB=P,且PA?γ,PB?γ,
∴l⊥γ.
证法二在α内作直线m垂直于α与γ的交线,在β内作直线n垂直于β与γ的交线,
∵α⊥γ,β⊥γ,∴m⊥γ,n⊥γ.
∴m∥n.
又n?β,m?β,∴m∥β.又m?α,α∩β=l,
∴m∥l.∴l⊥γ.探究一探究二思想方法方法点睛空间垂直关系的转化关系 1231.如图所示,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=PB,AD=DB,则( )
A.PD?平面ABC
B.PD⊥平面ABC
C.PD与平面ABC相交但不垂直
D.PD∥平面ABC
解析:∵PA=PB,AD=DB,∴PD⊥AB.
又平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD?平面PAB,∴PD⊥平面ABC.
答案:B1232.已知直线m,n和平面α,β,若α⊥β,α∩β=m,n?α,要使n⊥β,则应增加的条件是( )
A.m∥n B.n⊥m
C.n∥α D.n⊥α
解析:已知直线m,n和平面α,β,若α⊥β,α∩β=m,m?α,应增加条件n⊥m,才能使得n⊥β.
答案:B1233.如图,四面体P-ABC中,PA=PB= ,平面PAB⊥平面ABC,∠ABC=90°,AC=8,BC=6,则PC= .?解析:取AB的中点E,连接PE.
∵PA=PB,∴PE⊥AB.
又平面PAB⊥平面ABC,∴PE⊥平面ABC.
连接CE,∴PE⊥CE.7
1.在日常生活中常见到一排排和地面垂直的电线杆.一排电线杆中的每根电线杆都与地面垂直,那么这些电线杆之间存在什么位置关系呢?
提示:平行.一二2.直线与平面垂直的性质定理 3.做一做:直线n⊥平面α,n∥l,直线m?α,则l,m的位置关系是( )
A.相交 B.异面 C.平行 D.垂直
解析:由题意可知l⊥α,∴l⊥m.
答案:D一二二、平面与平面垂直的性质定理
1.黑板所在平面与地面所在平面垂直,你能否在黑板上画一条直线与地面垂直?
提示:容易发现墙壁与墙壁所在平面的交线与地面垂直,因此只要在黑板上画出一条与这条交线平行的直线,则所画直线必与地面垂直.一二2.填表:平面与平面垂直的性质定理 一二3.做一做:若平面α⊥平面β,平面β⊥平面γ,则 ( )
A.α∥γ
B.α⊥γ
C.α与γ相交但不垂直
D.以上都有可能
答案:D探究一探究二思想方法直线与平面垂直的性质的应用
例1如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证:MN∥AD1.
思路分析:两直线垂直于同一平面?两直线平行.
证明因为四边形ADD1A1为正方形,所以AD1⊥A1D.又因为CD⊥平面ADD1A1,所以CD⊥AD1.
因为A1D∩CD=D,所以AD1⊥平面A1DC.又因为MN⊥平面A1DC,所以MN∥AD1.探究一探究二思想方法反思感悟1.线面垂直的性质:应用直线与平面垂直的常见性质达到证明线线平行的目的,即线面垂直的性质提供了证明线线平行的依据.
2.直线与平面垂直的其他性质:
(1)若一条直线垂直于一个平面,则它就垂直于这个平面内的任意一条直线;
(2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面;
(3)若一条直线垂直于两个平行平面中的一个,则它必垂直于另一个平面;
(4)垂直于同一条直线的两个平面平行.探究一探究二思想方法延伸探究1本例中条件不变,求证:M是AB中点.
证明连接ON,在△A1DC中,A1O=OD,A1N=NC.
所以ON∥AM.
又因为由例题可知MN∥OA,
所以四边形AMNO为平行四边形,
所以ON=AM.
所以M是AB的中点.探究一探究二思想方法延伸探究2本例中把条件“MN⊥平面A1DC”改为“M是AB中点”,求证:MN⊥平面A1DC.
证明连接A1M,CM,取CD中点P,连接NP,MP,
由正方体AC1,M,N为中点,则A1M=CM,
所以MN⊥A1C.
又P为CD中点,所以PN∥A1D.
因为CD⊥A1D,所以CD⊥PN.
又MP⊥CD,MP∩PN=P,
所以CD⊥平面MPN.
因为MN?平面MPN,
所以MN⊥CD.
又A1C∩CD=C,
所以MN⊥平面A1DC.探究一探究二思想方法平面与平面垂直的性质的应用
例2 如图,已知V是△ABC外一点,VA⊥平面ABC,平面VAB⊥平面VBC.求证:AB⊥BC.
思路分析:要证AB⊥BC,可证BC⊥平面VAB,易得VA⊥BC.又平面VAB⊥平面VBC,所以可在平面VAB内过A作VB的垂线,即与BC垂直,可得证.探究一探究二思想方法证明:在平面VAB内,过点A作AD⊥VB于点D.
∵平面VAB⊥平面VBC,且交线为VB,
∴AD⊥平面VBC.∴AD⊥BC.
∵VA⊥平面ABC,∴VA⊥BC.
∵AD∩VA=A,且VA?平面VAB,AD?平面VAB,
∴BC⊥平面VAB.
∵AB?平面VAB,
∴AB⊥BC.探究一探究二思想方法反思感悟面面垂直的常见性质
1.在运用面面垂直的性质定理时,若没有与交线垂直的直线,一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线,这样便把面面垂直问题转化为线面垂直问题,进而转化为线线垂直问题.
2.平面与平面垂直的其他性质:
(1)如果两个平面垂直,那么经过第一个平面内一点垂直于第二个平面的直线在第一个平面内.
(2)如果两个平面垂直,那么与其中一个平面平行的平面垂直于另一个平面.
(3)如果两个平面垂直,那么其中一个平面的垂线平行于另一个平面或在另一个平面内.探究一探究二思想方法延伸探究【例2】中的已知换为:平面VAB⊥平面ABC,平面VAC⊥平面ABC,CA⊥AB.试证:VA⊥BC.
证明:∵平面VAB⊥平面ABC,
平面VAB∩平面ABC=AB,AC?平面ABC,CA⊥AB,
∴CA⊥平面VAB,∴CA⊥VA.
同理,BA⊥VA.
又AB∩AC=A,∴VA⊥平面ABC,
∵BC?平面ABC,∴VA⊥BC.探究一探究二思想方法转化思想在线线、线面、面面垂直中的应用
典例 已知α,β,γ是三个不同的平面,l为直线,α⊥γ,β⊥γ,α∩β=l.求证:l⊥γ.
【审题视角】 根据直线和平面垂直的判定定理,可在γ内构造两相交直线分别与平面α,β垂直;或者由面面垂直的性质易在α,β内作出平面γ的垂线,再设法证明l与其平行即可.探究一探究二思想方法证法一在γ内取一点P,作PA垂直α与γ的交线于点A,PB垂直β与γ的交线于点B,则PA⊥α,PB⊥β.
∵l=α∩β,
∴l⊥PA,l⊥PB.
又PA∩PB=P,且PA?γ,PB?γ,
∴l⊥γ.
证法二在α内作直线m垂直于α与γ的交线,在β内作直线n垂直于β与γ的交线,
∵α⊥γ,β⊥γ,∴m⊥γ,n⊥γ.
∴m∥n.
又n?β,m?β,∴m∥β.又m?α,α∩β=l,
∴m∥l.∴l⊥γ.探究一探究二思想方法方法点睛空间垂直关系的转化关系 1231.如图所示,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=PB,AD=DB,则( )
A.PD?平面ABC
B.PD⊥平面ABC
C.PD与平面ABC相交但不垂直
D.PD∥平面ABC
解析:∵PA=PB,AD=DB,∴PD⊥AB.
又平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD?平面PAB,∴PD⊥平面ABC.
答案:B1232.已知直线m,n和平面α,β,若α⊥β,α∩β=m,n?α,要使n⊥β,则应增加的条件是( )
A.m∥n B.n⊥m
C.n∥α D.n⊥α
解析:已知直线m,n和平面α,β,若α⊥β,α∩β=m,m?α,应增加条件n⊥m,才能使得n⊥β.
答案:B1233.如图,四面体P-ABC中,PA=PB= ,平面PAB⊥平面ABC,∠ABC=90°,AC=8,BC=6,则PC= .?解析:取AB的中点E,连接PE.
∵PA=PB,∴PE⊥AB.
又平面PAB⊥平面ABC,∴PE⊥平面ABC.
连接CE,∴PE⊥CE.7
