4.2.1直线与圆的位置关系课件(25张)
文档属性
| 名称 | 4.2.1直线与圆的位置关系课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 1014.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 13:33:33 | ||
图片预览








文档简介
课件25张PPT。4.2 直线、圆的位置关系4.2.1 直线与圆的位置关系直线与圆的位置关系的判定方法
1.大海上初升的红日,冉冉升起中,展现着迷人的风采,同时也体现了直线与圆的三种位置关系:相交、相切、相离.
(1)怎样用圆心到直线的距离d与圆的半径r的大小关系来判断直线与圆的位置关系?
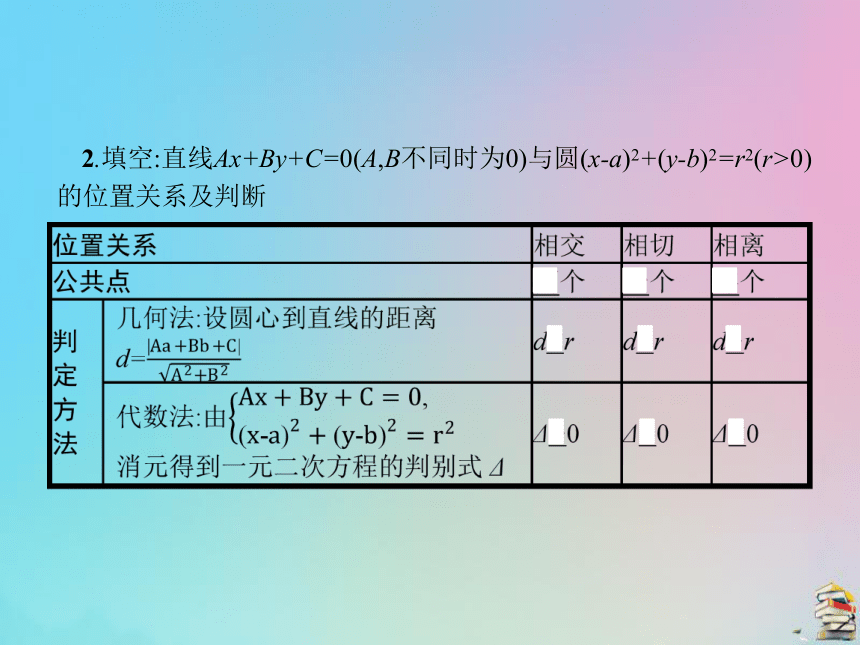
提示:利用圆心到直线的距离d与圆半径r的大小关系判断它们之间的位置关系如下:若d>r,则直线与圆相离;若d=r,则直线与圆相切;若d提示:把直线的方程与圆的方程组成方程组当方程组无解即Δ<0时,直线与圆相离;方程组有一解即Δ=0时,直线与圆相切;方程组有两解即Δ>0时,直线与圆相交.2.填空:直线Ax+By+C=0(A,B不同时为0)与圆(x-a)2+(y-b)2=r2(r>0)的位置关系及判断3.做一做:
(1)直线3x+4y=5与圆x2+y2=16的位置关系是 ( )
A.相交 B.相切
C.相离 D.相切或相交答案:A
(2)过原点作圆x2+y2-2x-2y+1=0的切线,切线方程为 .?
解析:∵圆的方程为(x-1)2+(y-1)2=1,
∴圆与x轴、y轴都相切,
∴所求切线方程为x=0或y=0.
答案:x=0或y=0探究一探究二探究三思想方法判断直线与圆的位置关系
例1 已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,直线与圆
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点?
思路分析:可联立方程组,由方程组解的个数判断,也可求出圆心到直线的距离,通过与半径比较大小判断.探究一探究二探究三思想方法解法一将直线mx-y-m-1=0代入圆的方程,化简、整理,
得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.探究一探究二探究三思想方法反思感悟直线与圆的位置关系的判断方法
直线与圆的位置关系反映在三个方面:一是点到直线的距离与半径大小的关系;二是直线与圆的公共点的个数;三是两方程组成的方程组解的个数.因此,若给出图形,可根据公共点的个数判断;若给出直线与圆的方程,可选择用几何法或代数法,几何法计算量小,代数法可一同求出交点.解题时可根据条件作出恰当的选择.探究一探究二探究三思想方法直线与圆相切
例2 过点A(4,-3)作圆C:(x-3)2+(y-1)2=1的切线,求此切线的方程.
思路分析:利用圆心到切线的距离等于圆的半径求出切线斜率,进而求出切线方程.解:因为(4-3)2+(-3-1)2=17>1,所以点A在圆外.
(1)若所求切线的斜率存在,设切线斜率为k,
则切线方程为y+3=k(x-4).
因为圆心C(3,1)到切线的距离等于半径,半径为1,探究一探究二探究三思想方法(2)若直线斜率不存在,
圆心C(3,1)到直线x=4的距离也为1,
这时直线与圆也相切,所以另一条切线方程是x=4.
综上,所求切线方程为15x+8y-36=0或x=4.
反思感悟切线方程的求法
1.求过圆上一点P(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,则由垂直关系,切线斜率为- ,由点斜式方程可求得切线方程.若k=0或斜率不存在,则由图形可直接得切线方程为y=b或x=a.
2.求过圆外一点P(x0,y0)的圆的切线时,常用几何方法求解
设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0,由圆心到直线的距离等于半径,可求得k,进而切线方程即可求出.但要注意,此时的切线有两条,若求出的k值只有一个时,则另一条切线的斜率一定不存在,可数形结合求出.探究一探究二探究三思想方法延伸探究过点Q(3,0)作圆x2+y2=4的切线,求此切线方程.
解:容易判断点Q(3,0)在圆外.设切线的方程为y=k(x-3),即kx-y-3k=0.又圆的圆心为(0,0),半径为2,探究一探究二探究三思想方法直线与圆相交
例3 求直线l:3x+y-6=0被圆C:x2+y2-2y-4=0截得的弦长.
思路分析:解法一求出直线与圆的交点坐标,解法二利用弦长公式,解法三利用几何法作出直角三角形,三种解法都可求得弦长.探究一探究二探究三思想方法消去y,得x2-3x+2=0.
设两交点A,B的坐标分别为A(x1,y1),B(x2,y2),则由根与系数的关系,得x1+x2=3,x1·x2=2.探究一探究二探究三思想方法反思感悟求直线与圆相交时弦长的两种方法
(1)几何法:如图①,直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,探究一探究二探究三思想方法(2)代数法:如图②所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A(x1,y1),B(x2,y2),探究一探究二探究三思想方法延伸探究已知直线l经过直线2x-y-3=0和4x-3y-5=0的交点,且与直线x+y-2=0垂直.
(1)求直线l的方程;
(2)若圆C的圆心为点(3,0),直线l被该圆所截得的弦长为2 ,求圆C的标准方程.探究一探究二探究三思想方法探究一探究二探究三思想方法数形结合法求参数的取值范围
典例已知直线l:y=x+b,与曲线C: 有两个不同的公共点,求实数b的取值范围.
解如图.
方程y=x+b表示斜率为1,在y轴上截距为b的直线,
防范措施有关直线与圆的位置关系问题,要看清运动中的不变量,例如本例中直线的平行关系,并注意方程中变量的取值范围.探究一探究二探究三思想方法12341.直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是( )
A.过圆心 B.相切
C.相离 D.相交但不过圆心
答案:D12342.若直线x+y+m=0与圆x2+y2=m相切,则m的值是 ( ) 解析:∵直线x+y+m=0与圆x2+y2=m相切, 答案:B 12343.(2018·全国1,文15)直线y=x+1与圆x2+y2+2y-3=0交于A,B两点,则|AB|= .?
解析:圆的方程可化为x2+(y+1)2=4,故圆心C(0,-1),半径r=2,圆心到12344.以点P(-4,3)为圆心的圆与直线l:2x+y-5=0相交,则圆的半径r的取值范围是 .?
解析:因为直线与圆相交,
所以圆心到直线的距离小于半径,
1.大海上初升的红日,冉冉升起中,展现着迷人的风采,同时也体现了直线与圆的三种位置关系:相交、相切、相离.
(1)怎样用圆心到直线的距离d与圆的半径r的大小关系来判断直线与圆的位置关系?
提示:利用圆心到直线的距离d与圆半径r的大小关系判断它们之间的位置关系如下:若d>r,则直线与圆相离;若d=r,则直线与圆相切;若d
(1)直线3x+4y=5与圆x2+y2=16的位置关系是 ( )
A.相交 B.相切
C.相离 D.相切或相交答案:A
(2)过原点作圆x2+y2-2x-2y+1=0的切线,切线方程为 .?
解析:∵圆的方程为(x-1)2+(y-1)2=1,
∴圆与x轴、y轴都相切,
∴所求切线方程为x=0或y=0.
答案:x=0或y=0探究一探究二探究三思想方法判断直线与圆的位置关系
例1 已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,直线与圆
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点?
思路分析:可联立方程组,由方程组解的个数判断,也可求出圆心到直线的距离,通过与半径比较大小判断.探究一探究二探究三思想方法解法一将直线mx-y-m-1=0代入圆的方程,化简、整理,
得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.探究一探究二探究三思想方法反思感悟直线与圆的位置关系的判断方法
直线与圆的位置关系反映在三个方面:一是点到直线的距离与半径大小的关系;二是直线与圆的公共点的个数;三是两方程组成的方程组解的个数.因此,若给出图形,可根据公共点的个数判断;若给出直线与圆的方程,可选择用几何法或代数法,几何法计算量小,代数法可一同求出交点.解题时可根据条件作出恰当的选择.探究一探究二探究三思想方法直线与圆相切
例2 过点A(4,-3)作圆C:(x-3)2+(y-1)2=1的切线,求此切线的方程.
思路分析:利用圆心到切线的距离等于圆的半径求出切线斜率,进而求出切线方程.解:因为(4-3)2+(-3-1)2=17>1,所以点A在圆外.
(1)若所求切线的斜率存在,设切线斜率为k,
则切线方程为y+3=k(x-4).
因为圆心C(3,1)到切线的距离等于半径,半径为1,探究一探究二探究三思想方法(2)若直线斜率不存在,
圆心C(3,1)到直线x=4的距离也为1,
这时直线与圆也相切,所以另一条切线方程是x=4.
综上,所求切线方程为15x+8y-36=0或x=4.
反思感悟切线方程的求法
1.求过圆上一点P(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,则由垂直关系,切线斜率为- ,由点斜式方程可求得切线方程.若k=0或斜率不存在,则由图形可直接得切线方程为y=b或x=a.
2.求过圆外一点P(x0,y0)的圆的切线时,常用几何方法求解
设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0,由圆心到直线的距离等于半径,可求得k,进而切线方程即可求出.但要注意,此时的切线有两条,若求出的k值只有一个时,则另一条切线的斜率一定不存在,可数形结合求出.探究一探究二探究三思想方法延伸探究过点Q(3,0)作圆x2+y2=4的切线,求此切线方程.
解:容易判断点Q(3,0)在圆外.设切线的方程为y=k(x-3),即kx-y-3k=0.又圆的圆心为(0,0),半径为2,探究一探究二探究三思想方法直线与圆相交
例3 求直线l:3x+y-6=0被圆C:x2+y2-2y-4=0截得的弦长.
思路分析:解法一求出直线与圆的交点坐标,解法二利用弦长公式,解法三利用几何法作出直角三角形,三种解法都可求得弦长.探究一探究二探究三思想方法消去y,得x2-3x+2=0.
设两交点A,B的坐标分别为A(x1,y1),B(x2,y2),则由根与系数的关系,得x1+x2=3,x1·x2=2.探究一探究二探究三思想方法反思感悟求直线与圆相交时弦长的两种方法
(1)几何法:如图①,直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,探究一探究二探究三思想方法(2)代数法:如图②所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A(x1,y1),B(x2,y2),探究一探究二探究三思想方法延伸探究已知直线l经过直线2x-y-3=0和4x-3y-5=0的交点,且与直线x+y-2=0垂直.
(1)求直线l的方程;
(2)若圆C的圆心为点(3,0),直线l被该圆所截得的弦长为2 ,求圆C的标准方程.探究一探究二探究三思想方法探究一探究二探究三思想方法数形结合法求参数的取值范围
典例已知直线l:y=x+b,与曲线C: 有两个不同的公共点,求实数b的取值范围.
解如图.
方程y=x+b表示斜率为1,在y轴上截距为b的直线,
防范措施有关直线与圆的位置关系问题,要看清运动中的不变量,例如本例中直线的平行关系,并注意方程中变量的取值范围.探究一探究二探究三思想方法12341.直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是( )
A.过圆心 B.相切
C.相离 D.相交但不过圆心
答案:D12342.若直线x+y+m=0与圆x2+y2=m相切,则m的值是 ( ) 解析:∵直线x+y+m=0与圆x2+y2=m相切, 答案:B 12343.(2018·全国1,文15)直线y=x+1与圆x2+y2+2y-3=0交于A,B两点,则|AB|= .?
解析:圆的方程可化为x2+(y+1)2=4,故圆心C(0,-1),半径r=2,圆心到12344.以点P(-4,3)为圆心的圆与直线l:2x+y-5=0相交,则圆的半径r的取值范围是 .?
解析:因为直线与圆相交,
所以圆心到直线的距离小于半径,
