4.2.3直线与圆的方程的应用课件 (17张)
文档属性
| 名称 | 4.2.3直线与圆的方程的应用课件 (17张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 13:30:26 | ||
图片预览




文档简介
课件17张PPT。4.2.3 直线与圆的方程的应用直线与圆的方程的应用
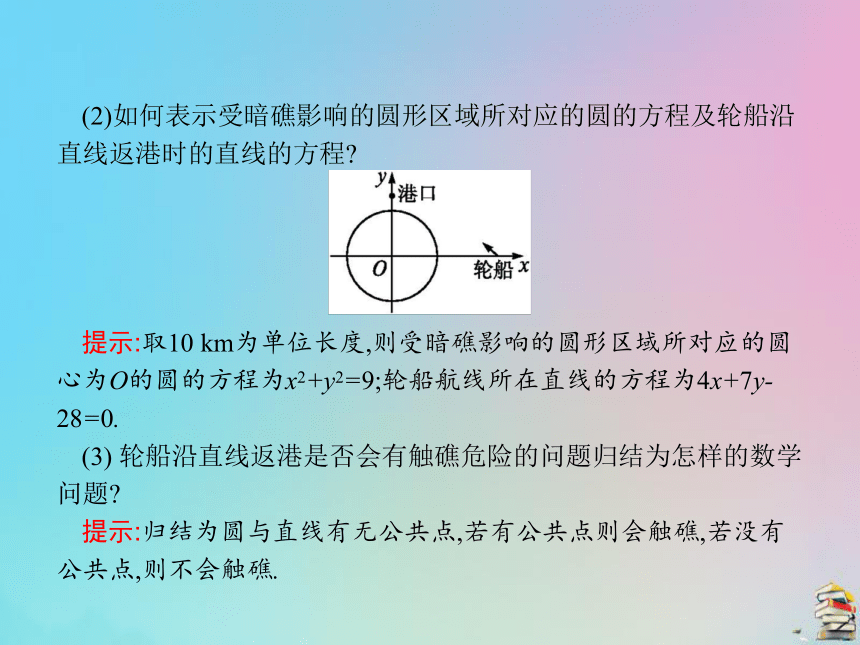
1.一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为30 km的圆形区域.已知小岛中心位于轮船正西70 km处,港口位于小岛中心正北40 km处.如果这艘轮船沿直线返港,那么它是否会有触礁危险?
(1)通过怎样的方法把这个实际问题转化为数学问题?
提示:以小岛的中心为原点O,东西方向为x轴,建立如图所示的平面直角坐标系.(2)如何表示受暗礁影响的圆形区域所对应的圆的方程及轮船沿直线返港时的直线的方程?
提示:取10 km为单位长度,则受暗礁影响的圆形区域所对应的圆心为O的圆的方程为x2+y2=9;轮船航线所在直线的方程为4x+7y-28=0.
(3) 轮船沿直线返港是否会有触礁危险的问题归结为怎样的数学问题?
提示:归结为圆与直线有无公共点,若有公共点则会触礁,若没有公共点,则不会触礁.2.填空:用直线与圆的方程解决实际问题的步骤
(1)从实际问题中提炼几何图形;
(2)建立直角坐标系,用坐标和方程表示问题中的几何元素,将平面问题转化为代数问题;
(3)通过代数运算,解决代数问题;
(4)将结果“翻译”成几何结论并作答.
3.用坐标方法解决几何问题的“三步曲”
(1)建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面问题转化为代数问题;
(2)通过代数运算,解决代数问题;
(3)将代数运算结果“翻译”成几何结论.探究一探究二思想方法直线与圆的方程的实际应用
例1 已知台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,求B城市处于危险区内的时间.
思路分析:将实际应用问题转化为直线与圆相交求弦长问题.
解:如图,以A为原点,以AB所在直线为x轴建立平面直角坐标系.
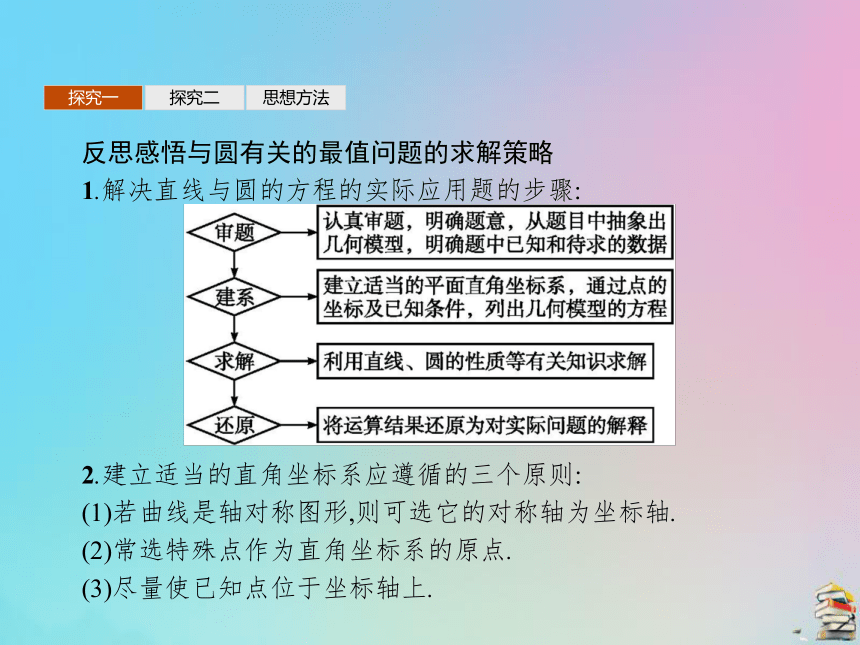
射线AC为∠xAy的平分线,则台风中心在射线AC上移动,则射线AC被以B为圆心,以30千米为半径的圆截得的弦长为 探究一探究二思想方法反思感悟与圆有关的最值问题的求解策略
1.解决直线与圆的方程的实际应用题的步骤: 2.建立适当的直角坐标系应遵循的三个原则:
(1)若曲线是轴对称图形,则可选它的对称轴为坐标轴.
(2)常选特殊点作为直角坐标系的原点.
(3)尽量使已知点位于坐标轴上.探究一探究二思想方法变式训练一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?解:以台风中心为坐标原点,以东西方向为x轴建立直角坐标系(如图),其中取10 km为单位长度,则受台风影响的圆形区域所对应的圆的方程为x2+y2=9,港口所对应的点的坐标为(0,4),轮船的初始位置所对应的点的坐标为(7,0),则轮船航线所在直线l的方程为改变航线,不会受到台风的影响. 探究一探究二思想方法与圆有关的最值问题
例2 已知实数x,y满足方程x2+y2-4x+1=0.求:(2)y-x的最大值和最小值;
(3)x2+y2的最大值和最小值.
思路分析:本题可将 和y-x转化成与直线斜率、截距有关的问题,x2+y2可看成是点(x,y)与点(0,0)距离的平方,然后结合图形求解.探究一探究二思想方法解:(1)如图,方程x2+y2-4x+1=0表示以点(2,0)为圆心,以 为半径的圆.易知圆心(2,0)到y=kx的距离等于半径时,直线与圆相切,斜率取得最大、最小值.(2)设y-x=b,则y=x+b,由点到直线的距离公式,探究一探究二思想方法(3)x2+y2表示圆上的一点与原点的距离的平方,由平面几何知识知,在原点和圆心的连线与圆的两个交点处取得最大值和最小值.反思感悟与圆有关的最值问题的求解策略
求与圆上的点的坐标有关的最值问题时,常常根据式子的结构特征,寻找它的几何意义,进而转化成与圆的性质有关的问题解决,其中构造斜率、截距、距离是最常用的方法.探究一探究二思想方法延伸探究若把例2中实数x,y满足的方程改为“(x-3)2+(y-3)2=6”,则
的最大值与最小值分别为 .?
解析:设P(x,y),则P点的轨迹就是已知圆C:(x-3)2+(y-3)2=6.探究一探究二思想方法函数思想解决与圆有关的最值问题
典例若动点(x,y)在圆x2+y2-4x=0上,求3x2+4y2的最大值.
解圆的方程可化为(x-2)2+y2=4,
所以y2=4x-x2,x∈[0,4].
所以3x2+4y2=3x2+4(4x-x2)=-x2+16x=-(x-8)2+64.因为x∈[0,4],
所以当x=4时,3x2+4y2取得最大值48.
防范措施用函数思想求与圆有关的最值问题时,一定注意不能忽略圆上的点(x,y)中的x,y的限制条件,也就是说要注意自变量的取值范围.12341.将直线x+y=1绕点(1,0)逆时针旋转90°后与圆x2+(y-1)2=r2(r>0)相切,则r的值是( )解析:将x+y=1绕点(1,0)逆时针旋转90°后,所得直线的方程为x- 答案:B 1234答案:D 12343.设村庄外围所在曲线的方程可用(x-2)2+(y+3)2=4表示,村外一小路方程可用x-y+2=0表示,则从村庄外围到小路的最短距离为 .?12344.一辆卡车宽1.6米,要经过一个半径为3.6米的半圆形隧道,则这辆卡车的平顶车篷篷顶距地面的高度不得超过 米.?
解析:如图是卡车在隧道内的截面图,由题意知OA=3.6米,AB=0.8米,答案:3.5
1.一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为30 km的圆形区域.已知小岛中心位于轮船正西70 km处,港口位于小岛中心正北40 km处.如果这艘轮船沿直线返港,那么它是否会有触礁危险?
(1)通过怎样的方法把这个实际问题转化为数学问题?
提示:以小岛的中心为原点O,东西方向为x轴,建立如图所示的平面直角坐标系.(2)如何表示受暗礁影响的圆形区域所对应的圆的方程及轮船沿直线返港时的直线的方程?
提示:取10 km为单位长度,则受暗礁影响的圆形区域所对应的圆心为O的圆的方程为x2+y2=9;轮船航线所在直线的方程为4x+7y-28=0.
(3) 轮船沿直线返港是否会有触礁危险的问题归结为怎样的数学问题?
提示:归结为圆与直线有无公共点,若有公共点则会触礁,若没有公共点,则不会触礁.2.填空:用直线与圆的方程解决实际问题的步骤
(1)从实际问题中提炼几何图形;
(2)建立直角坐标系,用坐标和方程表示问题中的几何元素,将平面问题转化为代数问题;
(3)通过代数运算,解决代数问题;
(4)将结果“翻译”成几何结论并作答.
3.用坐标方法解决几何问题的“三步曲”
(1)建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面问题转化为代数问题;
(2)通过代数运算,解决代数问题;
(3)将代数运算结果“翻译”成几何结论.探究一探究二思想方法直线与圆的方程的实际应用
例1 已知台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,求B城市处于危险区内的时间.
思路分析:将实际应用问题转化为直线与圆相交求弦长问题.
解:如图,以A为原点,以AB所在直线为x轴建立平面直角坐标系.
射线AC为∠xAy的平分线,则台风中心在射线AC上移动,则射线AC被以B为圆心,以30千米为半径的圆截得的弦长为 探究一探究二思想方法反思感悟与圆有关的最值问题的求解策略
1.解决直线与圆的方程的实际应用题的步骤: 2.建立适当的直角坐标系应遵循的三个原则:
(1)若曲线是轴对称图形,则可选它的对称轴为坐标轴.
(2)常选特殊点作为直角坐标系的原点.
(3)尽量使已知点位于坐标轴上.探究一探究二思想方法变式训练一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?解:以台风中心为坐标原点,以东西方向为x轴建立直角坐标系(如图),其中取10 km为单位长度,则受台风影响的圆形区域所对应的圆的方程为x2+y2=9,港口所对应的点的坐标为(0,4),轮船的初始位置所对应的点的坐标为(7,0),则轮船航线所在直线l的方程为改变航线,不会受到台风的影响. 探究一探究二思想方法与圆有关的最值问题
例2 已知实数x,y满足方程x2+y2-4x+1=0.求:(2)y-x的最大值和最小值;
(3)x2+y2的最大值和最小值.
思路分析:本题可将 和y-x转化成与直线斜率、截距有关的问题,x2+y2可看成是点(x,y)与点(0,0)距离的平方,然后结合图形求解.探究一探究二思想方法解:(1)如图,方程x2+y2-4x+1=0表示以点(2,0)为圆心,以 为半径的圆.易知圆心(2,0)到y=kx的距离等于半径时,直线与圆相切,斜率取得最大、最小值.(2)设y-x=b,则y=x+b,由点到直线的距离公式,探究一探究二思想方法(3)x2+y2表示圆上的一点与原点的距离的平方,由平面几何知识知,在原点和圆心的连线与圆的两个交点处取得最大值和最小值.反思感悟与圆有关的最值问题的求解策略
求与圆上的点的坐标有关的最值问题时,常常根据式子的结构特征,寻找它的几何意义,进而转化成与圆的性质有关的问题解决,其中构造斜率、截距、距离是最常用的方法.探究一探究二思想方法延伸探究若把例2中实数x,y满足的方程改为“(x-3)2+(y-3)2=6”,则
的最大值与最小值分别为 .?
解析:设P(x,y),则P点的轨迹就是已知圆C:(x-3)2+(y-3)2=6.探究一探究二思想方法函数思想解决与圆有关的最值问题
典例若动点(x,y)在圆x2+y2-4x=0上,求3x2+4y2的最大值.
解圆的方程可化为(x-2)2+y2=4,
所以y2=4x-x2,x∈[0,4].
所以3x2+4y2=3x2+4(4x-x2)=-x2+16x=-(x-8)2+64.因为x∈[0,4],
所以当x=4时,3x2+4y2取得最大值48.
防范措施用函数思想求与圆有关的最值问题时,一定注意不能忽略圆上的点(x,y)中的x,y的限制条件,也就是说要注意自变量的取值范围.12341.将直线x+y=1绕点(1,0)逆时针旋转90°后与圆x2+(y-1)2=r2(r>0)相切,则r的值是( )解析:将x+y=1绕点(1,0)逆时针旋转90°后,所得直线的方程为x- 答案:B 1234答案:D 12343.设村庄外围所在曲线的方程可用(x-2)2+(y+3)2=4表示,村外一小路方程可用x-y+2=0表示,则从村庄外围到小路的最短距离为 .?12344.一辆卡车宽1.6米,要经过一个半径为3.6米的半圆形隧道,则这辆卡车的平顶车篷篷顶距地面的高度不得超过 米.?
解析:如图是卡车在隧道内的截面图,由题意知OA=3.6米,AB=0.8米,答案:3.5
