1.2.1_1.2.2中心投影与平行投影空间几何体的三视图课件(29张)
文档属性
| 名称 | 1.2.1_1.2.2中心投影与平行投影空间几何体的三视图课件(29张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 15:34:09 | ||
图片预览







文档简介
课件29张PPT。1.2 空间几何体的三视图和直观图1.2.1~1.2.2 中心投影与平行投影 空间几何体的三视图一二一、投影的概念及分类
1.请同学们观察下面三组手影,思考一下它们是怎样形成的?
提示:光照射到手上,在墙上(或屏幕上)留下的影子.
2.不同的光源发出的光线是有差异的,其中灯泡发出的光线与手电筒发出的光线有什么不同?
提示:灯泡发出的光线是由一点向外分散发射的;手电筒发出的光是一束平行光线.一二3.用手电筒照射一个与投影面平行的不透明物体,在投影面上形成的影子与原物体的形状、大小有什么关系?当物体与手电筒的距离发生变化时,影子的大小会有变化吗?
提示:形状和大小是相同的;当物体与手电筒的距离发生变化时,影子的大小不变.
4.一个与投影面平行的平面图形,在正投影和斜投影下的形状、大小是否发生变化?一个与投影面不平行的平面图形,在正投影和斜投影下的形状、大小是否发生变化?
提示:与投影面平行的平面图形,在正投影和斜投影下形状、大小都不发生变化;与投影面不平行的平面图形,在正投影和斜投影下形状、大小会发生变化.一二5.关于投影的概念及分类,请完成下表: 一二6.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)一个点在一个平面内的投影仍是一个点.( )
(2)一条线段在一个平面内的投影仍是线段.( )
(3)一条直线在一个平面内的投影仍是一条直线.( )
(4)一个三角形在一个平面内的投影仍是三角形.( )
答案:(1)√ (2)× (3)× (4)×一二二、三视图的分类及画法规则
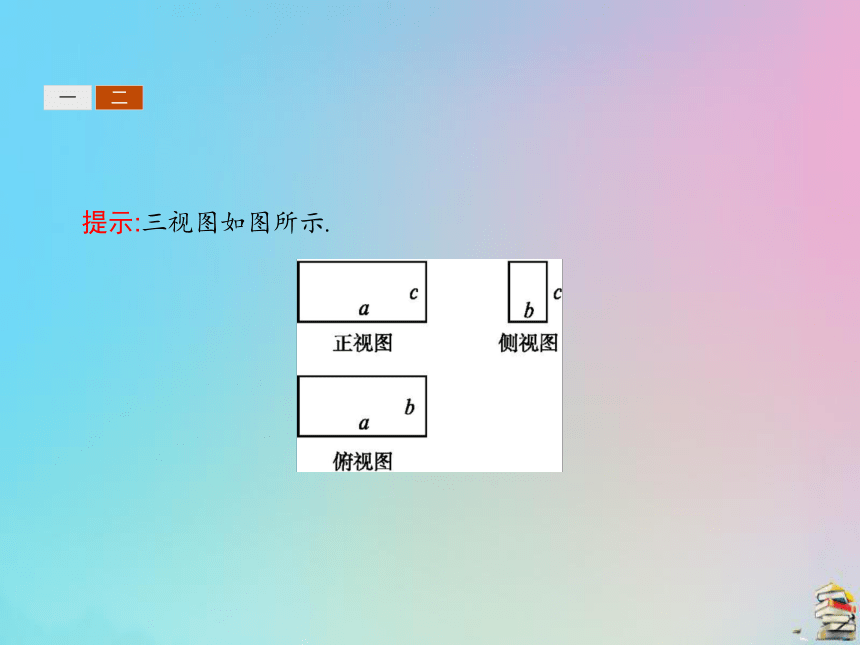
1.如梦似幻的“水立方”,不管从哪个方向来看,你都会被她婀娜多姿的风采所吸引.把一个空间几何体投影到一个平面上,可以获得一个平面图形,从多个角度进行投影就能较好地把握几何体的形状和大小,通常选择三种正投影,即正面、侧面和上面.你能画出如图所示的长方体的三视图吗?一二提示:三视图如图所示. 一二2.关于三视图的分类及画法规则,请完成下表: 一二3.做一做:如图,该几何体的俯视图是 (填序号).?
答案:②
4.在简单组合体中,从正视、侧视、俯视等角度观察,有些轮廓线和棱能看见,有些轮廓线和棱不能看见,在画三视图时怎样处理?
提示:能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.探究一探究二探究三思维辨析中心投影与平行投影
例1下列说法:
①平行投影的投影线互相平行,中心投影的投影线相交于一点;②空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线;③几何体在平行投影与中心投影下有不同的表现形式.
其中正确的个数为( )
A.0 B.1 C.2 D.3
解析:平行投影的投影线互相平行,中心投影的投影线相交于一点;空间图形经过中心投影后,直线变成直线,但平行线有可能变成相交线,如照片中由近到远物体之间的距离越来越近,最后相交于一点;几何体在平行投影与中心投影下有不同的表现形式.故3种说法都正确.
答案:D探究一探究二探究三思维辨析反思感悟中心投影与平行投影的判断方法
1.考察一个几何体的投影是什么图形,先分清楚是平行投影还是中心投影,投影面的位置如何,再根据平行投影或中心投影的性质来判断.
2.平行投影需注意图形、投射线、投射面之间的位置关系,位置发生改变,一般情况下投影也会改变.
3.中心投影与人的视觉效果一致,解题时可结合生活实际作出判断.探究一探究二探究三思维辨析变式训练 如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成的阴影(圆形)的示意图.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 m2(忽略桌脚).?
解析:设地面阴影圆的半径为x m,则有 ,解得x=0.9,故阴影圆的面积为S=πx2=0.81π(m2).
答案:0.81π探究一探究二探究三思维辨析空间几何体的三视图
例2 画出下列几何体的三视图.
思路分析:形体分析→确定方向→画三视图→排列方法探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟画三视图的基本步骤
(1)形体分析:是简单几何体还是简单组合体.如果是简单组合体的话,分析组合体是由哪几部分组成及各部分之间的相对位置.
(2)确定方向:画三视图时,要想象几何体的后面、右面、下面各有一个屏幕,一组平行光线分别从前面、左面、上面垂直照射,我们画的是影子的轮廓.
(3)排列方法:正视图与侧视图在同一水平位置,且正视图在左,侧视图在右,俯视图在正视图的正下方.探究一探究二探究三思维辨析变式训练画出下列几何体的三视图.
解:(1)为正六棱柱,正视图和侧视图都是矩形,正视图中有两条竖线,侧视图中有一条竖线,俯视图是正六边形.(2)为一个圆锥与一个圆台的组合体,按圆锥、圆台的三视图画出它们的组合形状.三视图如图.探究一探究二探究三思维辨析由三视图还原空间几何体
例3 根据下列图中所给出的几何体的三视图,试画出它们的形状.探究一探究二探究三思维辨析思路分析:结合图形,充分发挥空间想象力,先确定是什么几何体,再画出图形.
解:(1)对应的几何体是一个六棱锥,(2)对应的几何体是一个三棱柱,则所对应的空间几何体的图形分别如图所示.探究一探究二探究三思维辨析反思感悟1.由三视图还原空间几何体的策略:
(1)通过正视图和侧视图确定是柱体、锥体还是台体.若正视图和侧视图为矩形,则原几何体为柱体;若正视图和侧视图为等腰三角形,则原几何体为锥体;若正视图和侧视图为等腰梯形,则原几何体为台体.
(2)通过俯视图确定是多面体还是旋转体.若俯视图为多边形,则原几何体为多面体;若俯视图为圆,则原几何体为旋转体.
2.由三视图还原空间几何体的步骤:探究一探究二探究三思维辨析延伸探究若将本例(1)中的三视图改为如右三视图,试分析该几何体结构特征并画出物体的实物草图.
解:由三视图可知该几何体为四棱锥,其中左侧面与底面垂直,底面为直角梯形,对应空间几何体如下图:探究一探究二探究三思维辨析对三视图识别不清而致误
典例一个正三棱柱的三视图如图所示,求这个正三棱柱的底面面积.
点拨:先由几何体的三视图还原出原几何体,再根据几何体的特点求解.探究一探究二探究三思维辨析反思在本题中2 cm实为底面正三角形的高,常误认为是底面正三角形的边长而出错.
误区警示三视图还原成直观图时一定要抓住“长对正、高平齐、宽相等”的原则,搞清直观图和三视图中线段长度之间的关系,避免出错.12341.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可能是( )
A.球 B.三棱锥 C.正方体 D.圆柱
解析:圆柱的正视图和侧视图都是矩形,而俯视图为圆,不可能三个视图相同.
答案:D12342.如图,在正方体ABCD-A1B1C1D1中,E,F分别是AA1,C1D1的中点,G是正方形BCC1B1的中心,则四边形AGFE在该正方体的各个面上的正投影可能是图①②③④中的 .?答案:图①、图②、图③ 12343.如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱1234解析:如图,几何体为三棱柱.
答案:B12344.如图,在下列几何体中,正视图与侧视图都是长方形的是
(填序号).?
解析:②的侧视图是三角形,⑤的正视图和侧视图都是等腰梯形,其余的都符合条件.
答案:①③④
1.请同学们观察下面三组手影,思考一下它们是怎样形成的?
提示:光照射到手上,在墙上(或屏幕上)留下的影子.
2.不同的光源发出的光线是有差异的,其中灯泡发出的光线与手电筒发出的光线有什么不同?
提示:灯泡发出的光线是由一点向外分散发射的;手电筒发出的光是一束平行光线.一二3.用手电筒照射一个与投影面平行的不透明物体,在投影面上形成的影子与原物体的形状、大小有什么关系?当物体与手电筒的距离发生变化时,影子的大小会有变化吗?
提示:形状和大小是相同的;当物体与手电筒的距离发生变化时,影子的大小不变.
4.一个与投影面平行的平面图形,在正投影和斜投影下的形状、大小是否发生变化?一个与投影面不平行的平面图形,在正投影和斜投影下的形状、大小是否发生变化?
提示:与投影面平行的平面图形,在正投影和斜投影下形状、大小都不发生变化;与投影面不平行的平面图形,在正投影和斜投影下形状、大小会发生变化.一二5.关于投影的概念及分类,请完成下表: 一二6.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)一个点在一个平面内的投影仍是一个点.( )
(2)一条线段在一个平面内的投影仍是线段.( )
(3)一条直线在一个平面内的投影仍是一条直线.( )
(4)一个三角形在一个平面内的投影仍是三角形.( )
答案:(1)√ (2)× (3)× (4)×一二二、三视图的分类及画法规则
1.如梦似幻的“水立方”,不管从哪个方向来看,你都会被她婀娜多姿的风采所吸引.把一个空间几何体投影到一个平面上,可以获得一个平面图形,从多个角度进行投影就能较好地把握几何体的形状和大小,通常选择三种正投影,即正面、侧面和上面.你能画出如图所示的长方体的三视图吗?一二提示:三视图如图所示. 一二2.关于三视图的分类及画法规则,请完成下表: 一二3.做一做:如图,该几何体的俯视图是 (填序号).?
答案:②
4.在简单组合体中,从正视、侧视、俯视等角度观察,有些轮廓线和棱能看见,有些轮廓线和棱不能看见,在画三视图时怎样处理?
提示:能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.探究一探究二探究三思维辨析中心投影与平行投影
例1下列说法:
①平行投影的投影线互相平行,中心投影的投影线相交于一点;②空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线;③几何体在平行投影与中心投影下有不同的表现形式.
其中正确的个数为( )
A.0 B.1 C.2 D.3
解析:平行投影的投影线互相平行,中心投影的投影线相交于一点;空间图形经过中心投影后,直线变成直线,但平行线有可能变成相交线,如照片中由近到远物体之间的距离越来越近,最后相交于一点;几何体在平行投影与中心投影下有不同的表现形式.故3种说法都正确.
答案:D探究一探究二探究三思维辨析反思感悟中心投影与平行投影的判断方法
1.考察一个几何体的投影是什么图形,先分清楚是平行投影还是中心投影,投影面的位置如何,再根据平行投影或中心投影的性质来判断.
2.平行投影需注意图形、投射线、投射面之间的位置关系,位置发生改变,一般情况下投影也会改变.
3.中心投影与人的视觉效果一致,解题时可结合生活实际作出判断.探究一探究二探究三思维辨析变式训练 如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成的阴影(圆形)的示意图.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 m2(忽略桌脚).?
解析:设地面阴影圆的半径为x m,则有 ,解得x=0.9,故阴影圆的面积为S=πx2=0.81π(m2).
答案:0.81π探究一探究二探究三思维辨析空间几何体的三视图
例2 画出下列几何体的三视图.
思路分析:形体分析→确定方向→画三视图→排列方法探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟画三视图的基本步骤
(1)形体分析:是简单几何体还是简单组合体.如果是简单组合体的话,分析组合体是由哪几部分组成及各部分之间的相对位置.
(2)确定方向:画三视图时,要想象几何体的后面、右面、下面各有一个屏幕,一组平行光线分别从前面、左面、上面垂直照射,我们画的是影子的轮廓.
(3)排列方法:正视图与侧视图在同一水平位置,且正视图在左,侧视图在右,俯视图在正视图的正下方.探究一探究二探究三思维辨析变式训练画出下列几何体的三视图.
解:(1)为正六棱柱,正视图和侧视图都是矩形,正视图中有两条竖线,侧视图中有一条竖线,俯视图是正六边形.(2)为一个圆锥与一个圆台的组合体,按圆锥、圆台的三视图画出它们的组合形状.三视图如图.探究一探究二探究三思维辨析由三视图还原空间几何体
例3 根据下列图中所给出的几何体的三视图,试画出它们的形状.探究一探究二探究三思维辨析思路分析:结合图形,充分发挥空间想象力,先确定是什么几何体,再画出图形.
解:(1)对应的几何体是一个六棱锥,(2)对应的几何体是一个三棱柱,则所对应的空间几何体的图形分别如图所示.探究一探究二探究三思维辨析反思感悟1.由三视图还原空间几何体的策略:
(1)通过正视图和侧视图确定是柱体、锥体还是台体.若正视图和侧视图为矩形,则原几何体为柱体;若正视图和侧视图为等腰三角形,则原几何体为锥体;若正视图和侧视图为等腰梯形,则原几何体为台体.
(2)通过俯视图确定是多面体还是旋转体.若俯视图为多边形,则原几何体为多面体;若俯视图为圆,则原几何体为旋转体.
2.由三视图还原空间几何体的步骤:探究一探究二探究三思维辨析延伸探究若将本例(1)中的三视图改为如右三视图,试分析该几何体结构特征并画出物体的实物草图.
解:由三视图可知该几何体为四棱锥,其中左侧面与底面垂直,底面为直角梯形,对应空间几何体如下图:探究一探究二探究三思维辨析对三视图识别不清而致误
典例一个正三棱柱的三视图如图所示,求这个正三棱柱的底面面积.
点拨:先由几何体的三视图还原出原几何体,再根据几何体的特点求解.探究一探究二探究三思维辨析反思在本题中2 cm实为底面正三角形的高,常误认为是底面正三角形的边长而出错.
误区警示三视图还原成直观图时一定要抓住“长对正、高平齐、宽相等”的原则,搞清直观图和三视图中线段长度之间的关系,避免出错.12341.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可能是( )
A.球 B.三棱锥 C.正方体 D.圆柱
解析:圆柱的正视图和侧视图都是矩形,而俯视图为圆,不可能三个视图相同.
答案:D12342.如图,在正方体ABCD-A1B1C1D1中,E,F分别是AA1,C1D1的中点,G是正方形BCC1B1的中心,则四边形AGFE在该正方体的各个面上的正投影可能是图①②③④中的 .?答案:图①、图②、图③ 12343.如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱1234解析:如图,几何体为三棱柱.
答案:B12344.如图,在下列几何体中,正视图与侧视图都是长方形的是
(填序号).?
解析:②的侧视图是三角形,⑤的正视图和侧视图都是等腰梯形,其余的都符合条件.
答案:①③④
