1.3.2球的体积和表面积课件(20张)
文档属性
| 名称 | 1.3.2球的体积和表面积课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 758.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 00:00:00 | ||
图片预览








文档简介
课件20张PPT。1.3.2 球的体积和表面积球的体积和表面积
1.球的表面无法像柱、锥、台体一样展成平面图形,怎样求出球的表面积和体积呢?就目前我们已有的知识水平还解决不了,我们不妨先记住公式,做到熟练运用.设球的半径为R,则它的体积V= πR3,表面积S=4πR2.观察这两个公式,它们都有什么特点?
提示:这两个公式说明球的体积和表面积都由球的半径R唯一确定.其中球的体积是半径R的三次函数,球的表面积是半径R的二次函数,并且表面积为半径为R的圆面积的4倍.2.做一做:已知球的表面积是16π,则该球的体积为 .?
解析:设球的半径为R,则由题意可知4πR2=16π,解得R=2.所以球的半径为2,3.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)设球的截面圆上一点A,球心为O,截面圆心为O1,则△AO1O是以O1为直角顶点的直角三角形. ( )
(2)若将气球的半径扩大到原来的2倍,则它的体积增大到原来的4倍. ( )
(3)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径. ( )
答案:(1)√ (2)× (3)√探究一探究二探究三思想方法球的表面积和体积
例1过球面上三点A,B,C的截面到球心O的距离等于球的半径的一半,且AB=BC=CA=3 cm,求球的体积和表面积.
思路分析解决本题要充分利用已知条件,尤其是球半径,截面圆半径和球心距构成的直角三角形.探究一探究二探究三思想方法解:如图,设过A,B,C三点的截面为圆O',连接OO'、AO、AO'.
∵AB=BC=CA=3 cm,
∴O'为正三角形ABC的中心,
∵OO'⊥截面ABC,
∴OO'⊥AO',
探究一探究二探究三思想方法反思感悟球的表面积与体积的求法
因为球的表面积与体积都是球半径的函数,所以在解答这类问题时,设法求出球的半径是解题的关键.探究一探究二探究三思想方法变式训练若两球的表面积之差为48π,它们的半径之和为6,则两球的体积之差的绝对值为 .?解析:设两个球的半径分别为R,r(R>r), 探究一探究二探究三思想方法由三视图求与球有关的组合体的体积与表面积
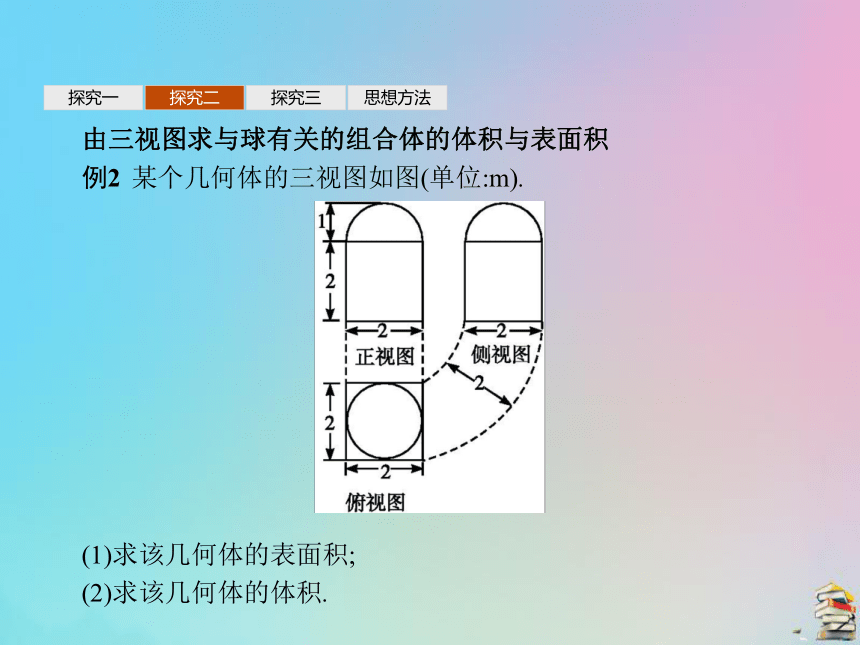
例2 某个几何体的三视图如图(单位:m).
(1)求该几何体的表面积;
(2)求该几何体的体积.探究一探究二探究三思想方法思路分析:本题条件中给出的是几何体的三视图及数据,解题时要先根据俯视图来确定几何体的上、下部分形状,再根据侧视图与正视图确定几何体的形状,最后根据有关数据计算.
解:由三视图可知,此几何体是由一个半径为1的半球和一个棱长为2的正方体组成.反思感悟球的组合体体积的计算方法
(1)由三视图求与球有关的组合体的表面积或体积时,最重要的是还原组合体,并弄清组合体的结构特征和三视图中数据的含义,根据组合体的结构特征及数据计算其表面积或体积.
(2)计算与球有关的组合体的表面积与体积时还要注意恰当地分割与拼接,避免重叠和交叉等.探究一探究二探究三思想方法与球有关的组合体
例3 各棱长均为 的四面体内有一内切球,求该球的体积.
思路分析:等体积法→内切球的半径→球的体积解:如图,在四面体S-ABC中,取底面△ABC的中心为O1,连接SO1,O1A,则SO1⊥O1A.探究一探究二探究三思想方法反思感悟常见的球的组合问题
与球有关的组合体一般有两类,一是与球内接的组合体,在此类组合体中,球心与多面体顶点的连线是半径;二是与球外切的组合体,在这一类组合体中,球心与各切点的连线是半径.在解答与球有关的组合体问题时,要注意这些半径的应用.探究一探究二探究三思想方法延伸探究求本例所给四面体外接球的表面积. 解:设外接球半径为R,由上述例题解题过程可知, 探究一探究二探究三思想方法转化与化归思想在球的接、切问题中的应用
典例 在半球内有一个内接正方体,试求这个半球的体积与正方体的体积之比.
【审题视角】 过正方体的对角面作一截面,在这个截面中用正方体的棱长、球半径的关系求解;或将球补为一个整球,利用球内接长方体求解.探究一探究二探究三思想方法解法一作正方体对角面的截面,如图所示,设半球的半径为R,正方体的棱长为a,探究一探究二探究三思想方法解法二将半球补成整个的球,同时把原半球的内接正方体再补接一个同样的正方体,构成的长方体刚好是这个球的内接长方体,则这个长方体的对角线便是它的外接球的直径.
设原正方体棱长为a,球的半径为R,则根据长方体的对角线性质,方法点睛球的轴截面(过球心的截面)是将球的问题(立体几何问题)转化为平面问题(圆的问题)的关键,因此在解决球的有关问题时,我们必须抓住球的轴截面,并充分利用它来分析解决问题.12341.若两球的体积之和是12π,经过两球球心的截面圆周长之和为6π,则两球的半径之差为( )
A.1 B.2 C.3 D.4
解析:设两球的半径分别为R,r(R>r),
则由题意得
∴R-r=1.
答案:A12342.若把球的表面积扩大到原来的2倍,则体积扩大到原来的( )倍. 解析:设球变化前后的半径分别为r与r', 答案:B 12343.把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为 .?答案:4R 12344.一个正方体的外接球、正方体、正方体的内切球的表面积之比为 .?解析:设正方体的棱长为2a,外接球半径为R,内切球半径为r, 所以,外接球、正方体、内切球的表面积之比为S1∶S2∶S3=(4πR2)∶[6×(2a)2]∶(4πr2)=[4π( a)2]∶(24a2)∶(4πa2)=12π∶24∶4π=3π∶6∶π.
答案:3π∶6∶π
1.球的表面无法像柱、锥、台体一样展成平面图形,怎样求出球的表面积和体积呢?就目前我们已有的知识水平还解决不了,我们不妨先记住公式,做到熟练运用.设球的半径为R,则它的体积V= πR3,表面积S=4πR2.观察这两个公式,它们都有什么特点?
提示:这两个公式说明球的体积和表面积都由球的半径R唯一确定.其中球的体积是半径R的三次函数,球的表面积是半径R的二次函数,并且表面积为半径为R的圆面积的4倍.2.做一做:已知球的表面积是16π,则该球的体积为 .?
解析:设球的半径为R,则由题意可知4πR2=16π,解得R=2.所以球的半径为2,3.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)设球的截面圆上一点A,球心为O,截面圆心为O1,则△AO1O是以O1为直角顶点的直角三角形. ( )
(2)若将气球的半径扩大到原来的2倍,则它的体积增大到原来的4倍. ( )
(3)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径. ( )
答案:(1)√ (2)× (3)√探究一探究二探究三思想方法球的表面积和体积
例1过球面上三点A,B,C的截面到球心O的距离等于球的半径的一半,且AB=BC=CA=3 cm,求球的体积和表面积.
思路分析解决本题要充分利用已知条件,尤其是球半径,截面圆半径和球心距构成的直角三角形.探究一探究二探究三思想方法解:如图,设过A,B,C三点的截面为圆O',连接OO'、AO、AO'.
∵AB=BC=CA=3 cm,
∴O'为正三角形ABC的中心,
∵OO'⊥截面ABC,
∴OO'⊥AO',
探究一探究二探究三思想方法反思感悟球的表面积与体积的求法
因为球的表面积与体积都是球半径的函数,所以在解答这类问题时,设法求出球的半径是解题的关键.探究一探究二探究三思想方法变式训练若两球的表面积之差为48π,它们的半径之和为6,则两球的体积之差的绝对值为 .?解析:设两个球的半径分别为R,r(R>r), 探究一探究二探究三思想方法由三视图求与球有关的组合体的体积与表面积
例2 某个几何体的三视图如图(单位:m).
(1)求该几何体的表面积;
(2)求该几何体的体积.探究一探究二探究三思想方法思路分析:本题条件中给出的是几何体的三视图及数据,解题时要先根据俯视图来确定几何体的上、下部分形状,再根据侧视图与正视图确定几何体的形状,最后根据有关数据计算.
解:由三视图可知,此几何体是由一个半径为1的半球和一个棱长为2的正方体组成.反思感悟球的组合体体积的计算方法
(1)由三视图求与球有关的组合体的表面积或体积时,最重要的是还原组合体,并弄清组合体的结构特征和三视图中数据的含义,根据组合体的结构特征及数据计算其表面积或体积.
(2)计算与球有关的组合体的表面积与体积时还要注意恰当地分割与拼接,避免重叠和交叉等.探究一探究二探究三思想方法与球有关的组合体
例3 各棱长均为 的四面体内有一内切球,求该球的体积.
思路分析:等体积法→内切球的半径→球的体积解:如图,在四面体S-ABC中,取底面△ABC的中心为O1,连接SO1,O1A,则SO1⊥O1A.探究一探究二探究三思想方法反思感悟常见的球的组合问题
与球有关的组合体一般有两类,一是与球内接的组合体,在此类组合体中,球心与多面体顶点的连线是半径;二是与球外切的组合体,在这一类组合体中,球心与各切点的连线是半径.在解答与球有关的组合体问题时,要注意这些半径的应用.探究一探究二探究三思想方法延伸探究求本例所给四面体外接球的表面积. 解:设外接球半径为R,由上述例题解题过程可知, 探究一探究二探究三思想方法转化与化归思想在球的接、切问题中的应用
典例 在半球内有一个内接正方体,试求这个半球的体积与正方体的体积之比.
【审题视角】 过正方体的对角面作一截面,在这个截面中用正方体的棱长、球半径的关系求解;或将球补为一个整球,利用球内接长方体求解.探究一探究二探究三思想方法解法一作正方体对角面的截面,如图所示,设半球的半径为R,正方体的棱长为a,探究一探究二探究三思想方法解法二将半球补成整个的球,同时把原半球的内接正方体再补接一个同样的正方体,构成的长方体刚好是这个球的内接长方体,则这个长方体的对角线便是它的外接球的直径.
设原正方体棱长为a,球的半径为R,则根据长方体的对角线性质,方法点睛球的轴截面(过球心的截面)是将球的问题(立体几何问题)转化为平面问题(圆的问题)的关键,因此在解决球的有关问题时,我们必须抓住球的轴截面,并充分利用它来分析解决问题.12341.若两球的体积之和是12π,经过两球球心的截面圆周长之和为6π,则两球的半径之差为( )
A.1 B.2 C.3 D.4
解析:设两球的半径分别为R,r(R>r),
则由题意得
∴R-r=1.
答案:A12342.若把球的表面积扩大到原来的2倍,则体积扩大到原来的( )倍. 解析:设球变化前后的半径分别为r与r', 答案:B 12343.把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为 .?答案:4R 12344.一个正方体的外接球、正方体、正方体的内切球的表面积之比为 .?解析:设正方体的棱长为2a,外接球半径为R,内切球半径为r, 所以,外接球、正方体、内切球的表面积之比为S1∶S2∶S3=(4πR2)∶[6×(2a)2]∶(4πr2)=[4π( a)2]∶(24a2)∶(4πa2)=12π∶24∶4π=3π∶6∶π.
答案:3π∶6∶π
