3.1.2两条直线平行与垂直的判定课件(27张)
文档属性
| 名称 | 3.1.2两条直线平行与垂直的判定课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 15:42:59 | ||
图片预览






文档简介
课件27张PPT。3.1.2 两条直线平行与垂直的判定一二一、两条直线平行与斜率之间的关系
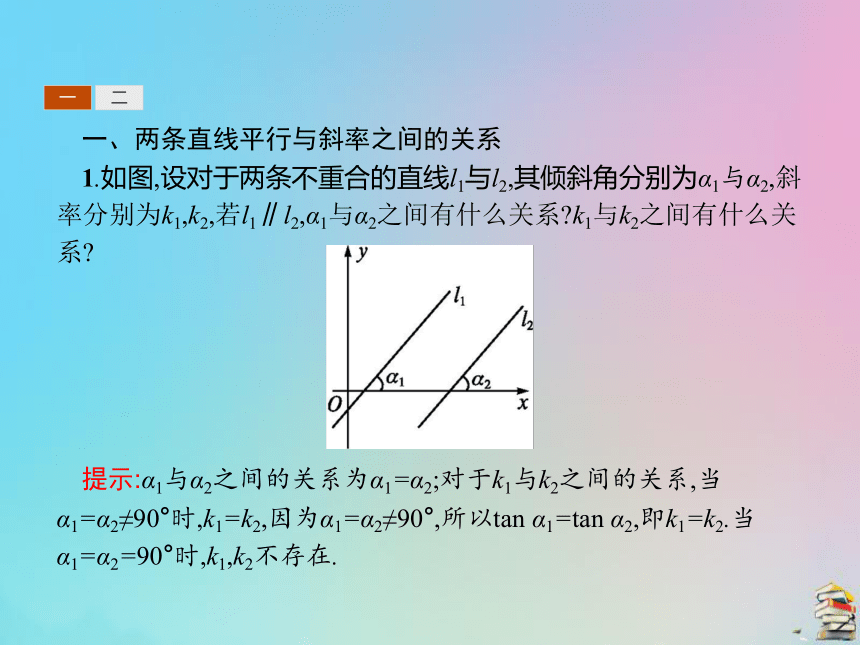
1.如图,设对于两条不重合的直线l1与l2,其倾斜角分别为α1与α2,斜率分别为k1,k2,若l1∥l2,α1与α2之间有什么关系?k1与k2之间有什么关系?
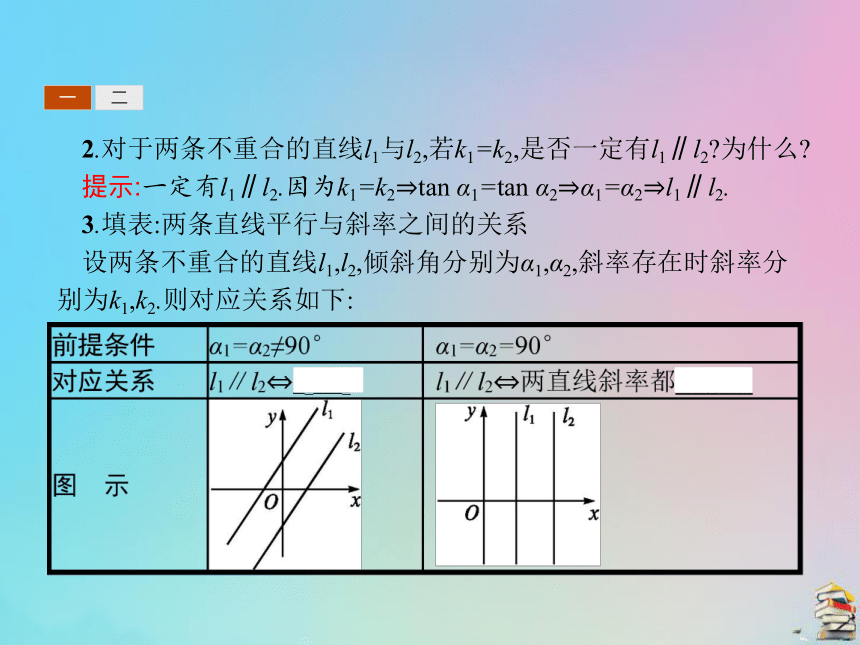
提示:α1与α2之间的关系为α1=α2;对于k1与k2之间的关系,当α1=α2≠90°时,k1=k2,因为α1=α2≠90°,所以tan α1=tan α2,即k1=k2.当α1=α2=90°时,k1,k2不存在.一二2.对于两条不重合的直线l1与l2,若k1=k2,是否一定有l1∥l2?为什么?
提示:一定有l1∥l2.因为k1=k2?tan α1=tan α2?α1=α2?l1∥l2.
3.填表:两条直线平行与斜率之间的关系
设两条不重合的直线l1,l2,倾斜角分别为α1,α2,斜率存在时斜率分别为k1,k2.则对应关系如下:一二4.做一做:已知直线l1经过两点(-1,-2),(-1,4),直线l2经过两点(2,1),(x,6),且l1∥l2,则x= .?
解析:由题意知l1⊥x轴.又l1∥l2,所以l2⊥x轴,故x=2.
答案:25.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若两条直线斜率相等,则这两条直线平行.( )
(2)若l1∥l2,则k1=k2.( )
(3)若两直线中有一条直线的斜率不存在,另一条直线的斜率存在,则两直线相交.( )
(4)若两直线斜率都不存在,则两直线平行.( )
答案:(1)× (2)× (3)√ (4)×一二二、两条直线垂直与斜率之间的关系
1.如图,设直线l1与l2的倾斜角分别为α1与α2,斜率分别为k1,k2,且α1<α2,若l1⊥l2,α1与α2之间有什么关系?为什么?
提示:α2=90°+α1,因为三角形任意一外角等于不相邻两内角之和.一二2.如果两直线的斜率存在且满足k1·k2=-1,是否一定有l1⊥l2?为什么?
提示:一定有l1⊥l2.不妨设k2<0,即α2为钝角,因为k1·k2=-1,则有tan α2tan α1=-1,又0°≤α1<180°,0°≤α2<180°,
所以tan α2=tan(90°+α1),
则α2=90°+α1,所以l1⊥l2.
3.对任意两条直线,如果l1⊥l2,一定有k1·k2=-1吗?为什么?
提示:不一定,因为如果直线l1和l2分别平行于x,y轴,则k2不存在,所以k1·k2=-1不成立.一二4.填表:两条直线垂直与斜率的关系 5.做一做:已知直线l1,l2的斜率分别为k1,k2,且k1=2,l1⊥l2,则k2= .?探究一探究二探究三思想方法两直线平行
例1 判断下列各小题中的直线l1与l2是否平行:
(1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1);
(2)l1的斜率为1,l2经过点A(1,1),B(2,2);
(3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0);
(4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5).
思路分析:斜率存在的直线求出斜率,利用l1∥l2?k1=k2进行判断,两直线斜率都不存在的,可通过观察并结合图形得出结论.探究一探究二探究三思想方法则A,B,M不共线.故l1∥l2.
(4)由已知点的坐标,得l1与l2均与x轴垂直且不重合,故有l1∥l2.
反思感悟两直线平行的判定及应用
1.判定两直线是否平行时,应先看两直线的斜率是否存在,若都不存在,则平行(不重合的情况下);若存在,再看是否相等,若相等,则平行(不重合的情况下).
2.若已知两直线平行,求某参数值时,也应分斜率存在与不存在两种情况求解.探究一探究二探究三思想方法延伸探究已知A(-2,m),B(m,4),M(m+2,3),N(1,1),若AB∥MN,则m的值为 .?
解析:当m=-2时,直线AB的斜率不存在,而直线MN的斜率存在,MN与AB不平行,不合题意;
当m=-1时,直线MN的斜率不存在,而直线AB的斜率存在,MN与AB不平行,不合题意;当m=0或1时,由图形知,两直线不重合.综上,m的值为0或1.
答案:0或1探究一探究二探究三思想方法两直线垂直
例2 (1)直线l1经过点A(3,2),B(3,-1),直线l2经过点M(1,1),N(2,1),判断l1与l2是否垂直;
(2)已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,求a的值.
思路分析:(1)若斜率存在,求出斜率,利用垂直的条件判断;若一条直线的斜率不存在,再看另一条直线的斜率是否为0,若为0,则垂直.
(2)当两直线的斜率都存在时,由斜率之积等于-1求解;若一条直线的斜率不存在,由另一条直线的斜率为0求解.探究一探究二探究三思想方法解:(1)直线l1的斜率不存在,直线l2的斜率为0,所以l1⊥l2.
(2)由题意,知直线l2的斜率k2一定存在,直线l1的斜率可能不存在.
当直线l1的斜率不存在时,3=a-2,即a=5,此时k2=0,
则l1⊥l2,满足题意.
当直线l1的斜率k1存在时,a≠5,由斜率公式,综上所述,a的值为0或5.
反思感悟反思感悟两直线垂直的判定方法
两条直线垂直需判定k1k2=-1,使用它的前提条件是两条直线斜率都存在,若其中一条直线斜率不存在,另一条直线斜率为零,此时两直线也垂直,注意讨论的全面性.探究一探究二探究三思想方法变式训练已知定点A(-1,3),B(4,2),以AB为直径作圆,与x轴有交点P,则交点P的坐标是 .?
解析:设以AB为直径的圆与x轴的交点为P(x,0).
∵kPB≠0,kPA≠0,
∴kPA·kPB=-1,∴(x+1)(x-4)=-6,即x2-3x+2=0,
解得x=1或x=2.故点P的坐标为(1,0)或(2,0).
答案:(1,0)或(2,0)探究一探究二探究三思想方法两直线平行与垂直的综合应用
例3
如图所示,在平面直角坐标系中,四边形OPQR的顶点坐标按逆时针顺序依次为O(0,0),P(1,t),Q(1-2t,2+t),R(-2t,2),其中t>0.试判断四边形OPQR的形状.
思路分析:利用直线方程的系数关系,或两直线间的斜率关系,判断两直线的位置关系.探究一探究二探究三思想方法所以kOP=kRQ,kOR=kPQ,从而OP∥RQ,OR∥PQ.
所以四边形OPQR为平行四边形.
又kOP·kOR=-1,所以OP⊥OR,
故四边形OPQR为矩形.探究一探究二探究三思想方法延伸探究1将本例中的四个点,改为“A(-4,3),B(2,5),C(6,3),D(-3,0),顺次连接A,B,C,D四点,试判断四边形ABCD的形状.”
解由题意A,B,C,D四点在平面直角坐标系内的位置如图,
所以kAB=kCD,由图可知AB与CD不重合,
所以AB∥CD,由kAD≠kBC,所以AD与BC不平行.
又因为kAB·kAD= ×(-3)=-1,
所以AB⊥AD,故四边形ABCD为直角梯形.探究一探究二探究三思想方法延伸探究2将本例改为“已知矩形OPQR中四个顶点按逆时针顺序依次为O(0,0),P(1,t),Q(1-2t,2+t),试求顶点R的坐标.”
解因为OPQR为矩形,所以OQ的中点也是PR的中点.探究一探究二探究三思想方法反思感悟
1.利用两条直线平行或垂直判定几何图形的形状的步骤
探究一探究二探究三思想方法2.判定几何图形形状的注意点
(1)在顶点确定的前提下,判定几何图形的形状时,要先画图,猜测其形状,以明确证明的目标.
(2)证明两直线平行时,仅有k1=k2是不够的,还要注意排除两直线重合的情况.
(3)判断四边形形状,要依据四边形的特点,并且不会产生其他的情况.探究一探究二探究三思想方法分类讨论思想在平行与垂直中的应用
典例已知点A(0,3),B(-1,0),C(3,0),且四边形ABCD为直角梯形,求点D的坐标.
思路分析:分析题意可知,AB、BC都不可作为直角梯形的直角边,所以要考虑CD是直角梯形的直角边和AD是直角梯形的直角边这两种情况;设所求点D的坐标为(x,y),若CD是直角梯形的直角边,则BC⊥CD,AD⊥CD,根据已知可得kBC=0,CD的斜率不存在,从而有x=3;接下来再根据kAD=kBC即可得到关于x、y的方程,结合x的值即可求出y,那么点D的坐标便不难确定了,同理再分析AD是直角梯形的直角边的情况即可.探究一探究二探究三思想方法解设所求点D的坐标为(x,y),如图所示,由于kAB=3,kBC=0,
则kAB·kBC=0≠-1,即AB与BC不垂直,故AB、BC都不可作为直角梯形的直角边.
①若CD是直角梯形的直角边,则BC⊥CD,AD⊥CD,
∵kBC=0,∴CD的斜率不存在,从而有x=3.
又∵kAD=kBC,∴ =0,即y=3.此时AB与CD不平行.
故所求点D的坐标为(3,3).
②若AD是直角梯形的直角边,探究一探究二探究三思想方法反思感悟先由图形判断四边形各边的关系,再由斜率之间的关系完成求解.特别地,注意讨论所求问题的不同情况.探究一探究二探究三思想方法变式训练 顺次连接A(-4,3),B(2,5),C(6,3),D(-3,0)四点,判断四边形ABCD形状.
所以直线AD垂直于直线AB与CD,而且直线BC不平行于任何一条直线,所以四边形ABCD是直角梯形.1231.若直线l1的斜率为a,l1⊥l2,则直线l2的斜率为( )解析:若a≠0,则l2的斜率为- ;若a=0,则l2的斜率不存在.
答案:D1232.已知直线l1的倾斜角为45°,直线l1∥l2,且l2过点A(-2,-1)和B(3,a),则a的值为 .?答案:4 1233.已知△ABC的三个顶点分别是A(2,2),B(0,1),C(4,3),点D(m,1)在边BC的高所在的直线上,则实数m= .?
解析:设直线AD,BC的斜率分别为kAD,kBC,
由题意,得AD⊥BC,则有kAD·kBC=-1,
1.如图,设对于两条不重合的直线l1与l2,其倾斜角分别为α1与α2,斜率分别为k1,k2,若l1∥l2,α1与α2之间有什么关系?k1与k2之间有什么关系?
提示:α1与α2之间的关系为α1=α2;对于k1与k2之间的关系,当α1=α2≠90°时,k1=k2,因为α1=α2≠90°,所以tan α1=tan α2,即k1=k2.当α1=α2=90°时,k1,k2不存在.一二2.对于两条不重合的直线l1与l2,若k1=k2,是否一定有l1∥l2?为什么?
提示:一定有l1∥l2.因为k1=k2?tan α1=tan α2?α1=α2?l1∥l2.
3.填表:两条直线平行与斜率之间的关系
设两条不重合的直线l1,l2,倾斜角分别为α1,α2,斜率存在时斜率分别为k1,k2.则对应关系如下:一二4.做一做:已知直线l1经过两点(-1,-2),(-1,4),直线l2经过两点(2,1),(x,6),且l1∥l2,则x= .?
解析:由题意知l1⊥x轴.又l1∥l2,所以l2⊥x轴,故x=2.
答案:25.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若两条直线斜率相等,则这两条直线平行.( )
(2)若l1∥l2,则k1=k2.( )
(3)若两直线中有一条直线的斜率不存在,另一条直线的斜率存在,则两直线相交.( )
(4)若两直线斜率都不存在,则两直线平行.( )
答案:(1)× (2)× (3)√ (4)×一二二、两条直线垂直与斜率之间的关系
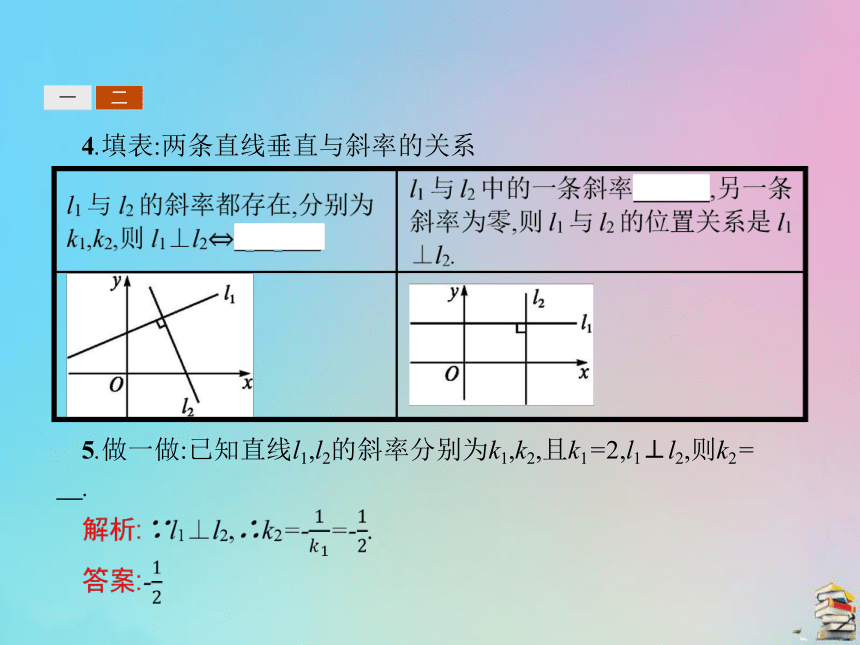
1.如图,设直线l1与l2的倾斜角分别为α1与α2,斜率分别为k1,k2,且α1<α2,若l1⊥l2,α1与α2之间有什么关系?为什么?
提示:α2=90°+α1,因为三角形任意一外角等于不相邻两内角之和.一二2.如果两直线的斜率存在且满足k1·k2=-1,是否一定有l1⊥l2?为什么?
提示:一定有l1⊥l2.不妨设k2<0,即α2为钝角,因为k1·k2=-1,则有tan α2tan α1=-1,又0°≤α1<180°,0°≤α2<180°,
所以tan α2=tan(90°+α1),
则α2=90°+α1,所以l1⊥l2.
3.对任意两条直线,如果l1⊥l2,一定有k1·k2=-1吗?为什么?
提示:不一定,因为如果直线l1和l2分别平行于x,y轴,则k2不存在,所以k1·k2=-1不成立.一二4.填表:两条直线垂直与斜率的关系 5.做一做:已知直线l1,l2的斜率分别为k1,k2,且k1=2,l1⊥l2,则k2= .?探究一探究二探究三思想方法两直线平行
例1 判断下列各小题中的直线l1与l2是否平行:
(1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1);
(2)l1的斜率为1,l2经过点A(1,1),B(2,2);
(3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0);
(4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5).
思路分析:斜率存在的直线求出斜率,利用l1∥l2?k1=k2进行判断,两直线斜率都不存在的,可通过观察并结合图形得出结论.探究一探究二探究三思想方法则A,B,M不共线.故l1∥l2.
(4)由已知点的坐标,得l1与l2均与x轴垂直且不重合,故有l1∥l2.
反思感悟两直线平行的判定及应用
1.判定两直线是否平行时,应先看两直线的斜率是否存在,若都不存在,则平行(不重合的情况下);若存在,再看是否相等,若相等,则平行(不重合的情况下).
2.若已知两直线平行,求某参数值时,也应分斜率存在与不存在两种情况求解.探究一探究二探究三思想方法延伸探究已知A(-2,m),B(m,4),M(m+2,3),N(1,1),若AB∥MN,则m的值为 .?
解析:当m=-2时,直线AB的斜率不存在,而直线MN的斜率存在,MN与AB不平行,不合题意;
当m=-1时,直线MN的斜率不存在,而直线AB的斜率存在,MN与AB不平行,不合题意;当m=0或1时,由图形知,两直线不重合.综上,m的值为0或1.
答案:0或1探究一探究二探究三思想方法两直线垂直
例2 (1)直线l1经过点A(3,2),B(3,-1),直线l2经过点M(1,1),N(2,1),判断l1与l2是否垂直;
(2)已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,求a的值.
思路分析:(1)若斜率存在,求出斜率,利用垂直的条件判断;若一条直线的斜率不存在,再看另一条直线的斜率是否为0,若为0,则垂直.
(2)当两直线的斜率都存在时,由斜率之积等于-1求解;若一条直线的斜率不存在,由另一条直线的斜率为0求解.探究一探究二探究三思想方法解:(1)直线l1的斜率不存在,直线l2的斜率为0,所以l1⊥l2.
(2)由题意,知直线l2的斜率k2一定存在,直线l1的斜率可能不存在.
当直线l1的斜率不存在时,3=a-2,即a=5,此时k2=0,
则l1⊥l2,满足题意.
当直线l1的斜率k1存在时,a≠5,由斜率公式,综上所述,a的值为0或5.
反思感悟反思感悟两直线垂直的判定方法
两条直线垂直需判定k1k2=-1,使用它的前提条件是两条直线斜率都存在,若其中一条直线斜率不存在,另一条直线斜率为零,此时两直线也垂直,注意讨论的全面性.探究一探究二探究三思想方法变式训练已知定点A(-1,3),B(4,2),以AB为直径作圆,与x轴有交点P,则交点P的坐标是 .?
解析:设以AB为直径的圆与x轴的交点为P(x,0).
∵kPB≠0,kPA≠0,
∴kPA·kPB=-1,∴(x+1)(x-4)=-6,即x2-3x+2=0,
解得x=1或x=2.故点P的坐标为(1,0)或(2,0).
答案:(1,0)或(2,0)探究一探究二探究三思想方法两直线平行与垂直的综合应用
例3
如图所示,在平面直角坐标系中,四边形OPQR的顶点坐标按逆时针顺序依次为O(0,0),P(1,t),Q(1-2t,2+t),R(-2t,2),其中t>0.试判断四边形OPQR的形状.
思路分析:利用直线方程的系数关系,或两直线间的斜率关系,判断两直线的位置关系.探究一探究二探究三思想方法所以kOP=kRQ,kOR=kPQ,从而OP∥RQ,OR∥PQ.
所以四边形OPQR为平行四边形.
又kOP·kOR=-1,所以OP⊥OR,
故四边形OPQR为矩形.探究一探究二探究三思想方法延伸探究1将本例中的四个点,改为“A(-4,3),B(2,5),C(6,3),D(-3,0),顺次连接A,B,C,D四点,试判断四边形ABCD的形状.”
解由题意A,B,C,D四点在平面直角坐标系内的位置如图,
所以kAB=kCD,由图可知AB与CD不重合,
所以AB∥CD,由kAD≠kBC,所以AD与BC不平行.
又因为kAB·kAD= ×(-3)=-1,
所以AB⊥AD,故四边形ABCD为直角梯形.探究一探究二探究三思想方法延伸探究2将本例改为“已知矩形OPQR中四个顶点按逆时针顺序依次为O(0,0),P(1,t),Q(1-2t,2+t),试求顶点R的坐标.”
解因为OPQR为矩形,所以OQ的中点也是PR的中点.探究一探究二探究三思想方法反思感悟
1.利用两条直线平行或垂直判定几何图形的形状的步骤
探究一探究二探究三思想方法2.判定几何图形形状的注意点
(1)在顶点确定的前提下,判定几何图形的形状时,要先画图,猜测其形状,以明确证明的目标.
(2)证明两直线平行时,仅有k1=k2是不够的,还要注意排除两直线重合的情况.
(3)判断四边形形状,要依据四边形的特点,并且不会产生其他的情况.探究一探究二探究三思想方法分类讨论思想在平行与垂直中的应用
典例已知点A(0,3),B(-1,0),C(3,0),且四边形ABCD为直角梯形,求点D的坐标.
思路分析:分析题意可知,AB、BC都不可作为直角梯形的直角边,所以要考虑CD是直角梯形的直角边和AD是直角梯形的直角边这两种情况;设所求点D的坐标为(x,y),若CD是直角梯形的直角边,则BC⊥CD,AD⊥CD,根据已知可得kBC=0,CD的斜率不存在,从而有x=3;接下来再根据kAD=kBC即可得到关于x、y的方程,结合x的值即可求出y,那么点D的坐标便不难确定了,同理再分析AD是直角梯形的直角边的情况即可.探究一探究二探究三思想方法解设所求点D的坐标为(x,y),如图所示,由于kAB=3,kBC=0,
则kAB·kBC=0≠-1,即AB与BC不垂直,故AB、BC都不可作为直角梯形的直角边.
①若CD是直角梯形的直角边,则BC⊥CD,AD⊥CD,
∵kBC=0,∴CD的斜率不存在,从而有x=3.
又∵kAD=kBC,∴ =0,即y=3.此时AB与CD不平行.
故所求点D的坐标为(3,3).
②若AD是直角梯形的直角边,探究一探究二探究三思想方法反思感悟先由图形判断四边形各边的关系,再由斜率之间的关系完成求解.特别地,注意讨论所求问题的不同情况.探究一探究二探究三思想方法变式训练 顺次连接A(-4,3),B(2,5),C(6,3),D(-3,0)四点,判断四边形ABCD形状.
所以直线AD垂直于直线AB与CD,而且直线BC不平行于任何一条直线,所以四边形ABCD是直角梯形.1231.若直线l1的斜率为a,l1⊥l2,则直线l2的斜率为( )解析:若a≠0,则l2的斜率为- ;若a=0,则l2的斜率不存在.
答案:D1232.已知直线l1的倾斜角为45°,直线l1∥l2,且l2过点A(-2,-1)和B(3,a),则a的值为 .?答案:4 1233.已知△ABC的三个顶点分别是A(2,2),B(0,1),C(4,3),点D(m,1)在边BC的高所在的直线上,则实数m= .?
解析:设直线AD,BC的斜率分别为kAD,kBC,
由题意,得AD⊥BC,则有kAD·kBC=-1,
