3.2.1直线的点斜式方程课件(21张)
文档属性
| 名称 | 3.2.1直线的点斜式方程课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 551.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 15:44:39 | ||
图片预览








文档简介
课件21张PPT。3.2 直线的方程3.2.1 直线的点斜式方程一二一、直线的点斜式方程
1.求直线的方程指的是求什么?
提示:就是求直线上任意一点的坐标(x,y)满足的关系等式.
2.如图,直线l经过点P0(x0,y0),且斜率为k,设点P(x,y)是直线l上不同于点P0的任意一点,怎样建立x,y之间的关系等式?该关系等式是直线l的方程吗?
提示:由斜率公式得k= ,即y-y0=k(x-x0),该关系等式是直线l的方程.一二3.填表:直线的点斜式方程 4.做一做:直线l的点斜式方程是y-2=3(x+1),则直线l的斜率是( )
A.2 B.-1 C.3 D.-3
答案:C一二二、直线的斜截式方程
1.已知直线l的斜率为k,且与y轴的交点为(0,b),则直线l的方程是什么?
提示:将k及点(0,b)代入直线的点斜式方程得y=kx+b.
2.直线y=kx+b在y轴上的截距b是直线与y轴交点到原点的距离吗?它的取值范围是什么?
提示:不是直线与y轴交点到原点的距离,是直线y=kx+b在y轴上交点的纵坐标,截距b的取值范围是R.
3.一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么不同?
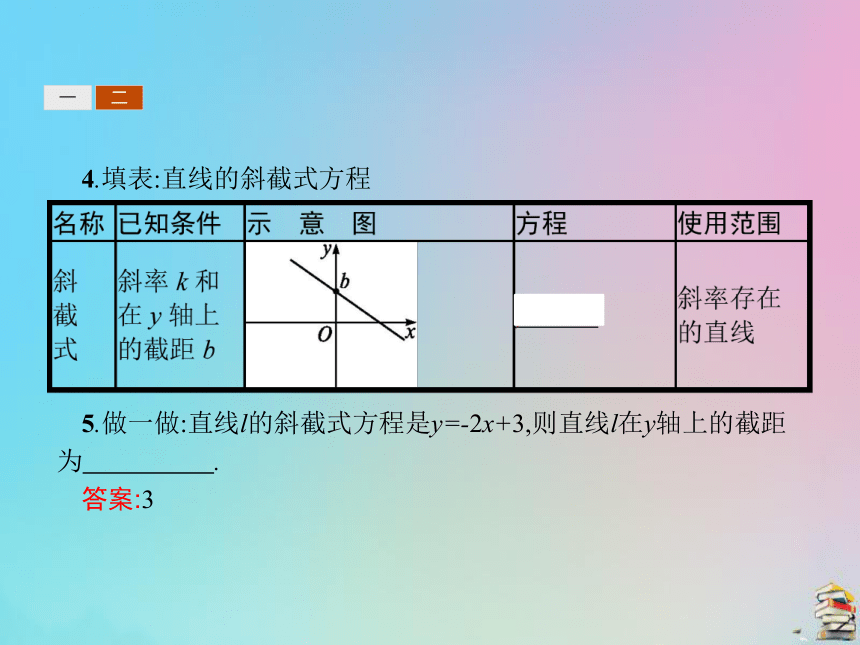
提示:一次函数的x的系数k≠0,否则就不是一次函数了;直线的斜截式方程y=kx+b中的k可以为0.一二4.填表:直线的斜截式方程 5.做一做:直线l的斜截式方程是y=-2x+3,则直线l在y轴上的截距为 .?
答案:3一二6.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)直线y-3=m(x+1)恒过定点(-1,3).( )
(2)直线y=2x+3在y轴上的截距为3.( )
答案:(1)√ (2)√探究一探究二思维辨析直线的点斜式方程
例1 求满足下列条件的直线方程:
(1)经过点(2,-3),倾斜角是直线y= x倾斜角的2倍;
(2)经过点P(5,-2),且与y轴平行;
(3)过P(-2,3),Q(5,-4)两点.
思路分析:先求出直线的斜率,然后由点斜式写出方程.探究一探究二思维辨析(2)与y轴平行的直线,其斜率k不存在,不能用点斜式方程表示.
但直线上点的横坐标均为5,
故直线方程可记为x=5.∵直线过点P(-2,3),
∴由直线的点斜式方程可得直线方程为y-3=-(x+2),即x+y-1=0.探究一探究二思维辨析反思感悟点斜式方程的求法
(1)求直线的点斜式方程,关键是求出直线的斜率,所以,已知直线上一点的坐标及直线的斜率或直线上两点坐标,均可求出直线的方程.
(2) 斜率不存在时,可直接写出过点(x0,y0)的直线方程x=x0.探究一探究二思维辨析变式训练直线l1的倾斜角为135°,直线l2经过点B(-1,4).求满足下列条件的直线l2的方程.
(1)直线l2∥l1;
(2)直线l2⊥l1.
解:(1)由已知直线l1的斜率k1=tan 135°=-1.
因为l2∥l1,所以直线l2的斜率k2=k1=-1.
又直线l2经过点B(-1,4),
代入点斜式方程得y-4=-1×[x-(-1)],即y=-x+3.
(2)由已知直线l1的斜率k1=tan 135°=-1.又直线l2经过点B(-1,4),
代入点斜式方程得y-4=1×[x-(-1)],即y=x+5.探究一探究二思维辨析直线的斜截式方程
例2 求满足下列条件的直线方程:
(1)经过点(0,-2),且与直线y=3x-5垂直;
(2)与直线y=-2x+3平行,与直线y=4x-2在y轴上的截距相同.
思路分析:写出直线的斜率及在y轴上的截距,用斜截式写出直线方程.探究一探究二思维辨析解:(1)因为直线y=3x-5的斜率为3,且所求直线与该直线垂直,所以所求直线斜率为- .
又直线过点(0,-2),由直线方程的斜截式,得
y=- x-2,即x+3y+6=0.
(2)直线y=-2x+3的斜率为-2,直线y=4x-2在y轴上的截距为-2.
由题意知,所求直线的斜率为-2,在y轴上的截距也为-2.
由直线方程的斜截式,得y=-2x-2,
即2x+y+2=0.
反思感悟斜截式方程的求法
已知直线的斜率与y轴上的截距,可直接写出直线的方程;已知直线的斜截式方程,可得直线的斜率与y轴上的截距.直线的斜截式方程形式简单,特点明显,是运用较多的直线方程的形式之一.探究一探究二思维辨析延伸探究直线l与直线l1:y=2x+6在y轴上有相同的截距,且l的斜率与l1的斜率互为相反数,则直线l的方程为 .?
解析:由直线l1的方程可知它的斜率为2,它在y轴上的截距为6,所以直线l的斜率为-2,在y轴上的截距为6.由直线的斜截式方程可得直线l的方程为y=-2x+6.
答案:y=-2x+6探究一探究二思维辨析误把“截距”当“距离”致错
典例 已知斜率为- 的直线l与两坐标轴围成的三角形面积为6,求直线l的方程.探究一探究二思维辨析防范措施①用斜截式表示直线方程前提条件是斜率存在,不能用斜截式表示与x轴垂直的直线.②把直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距.注意“截距非距”,即截距不是距离,截距可以取一切实数,即可为正数、零或负数.当直线l与y轴的正半轴相交时,其在y轴上的截距b>0;当直线l与y轴的负半轴相交时,其在y轴上的截距b<0;当直线l经过原点时,其在y轴上的截距b=0.当直线l与y轴平行时,l在y轴上没有截距.1234答案:B 12342.与直线y=3x+1垂直,且过点(2,-1)的直线的斜截式方程是( ) 答案:B 12343.无论k取何值,直线y-2=k(x+1)所过的定点是 .?
答案:(-1,2)12344.直线l1与直线l2:y=3x+1平行,又直线l1过点(3,5),则直线l1的方程为 .?
解析:∵直线l2的斜率k2=3,l1与l2平行,
∴直线l1的斜率k1=3.
又直线l1过点(3,5),
∴l1的方程为y-5=3(x-3),即y=3x-4.
答案:y=3x-4
1.求直线的方程指的是求什么?
提示:就是求直线上任意一点的坐标(x,y)满足的关系等式.
2.如图,直线l经过点P0(x0,y0),且斜率为k,设点P(x,y)是直线l上不同于点P0的任意一点,怎样建立x,y之间的关系等式?该关系等式是直线l的方程吗?
提示:由斜率公式得k= ,即y-y0=k(x-x0),该关系等式是直线l的方程.一二3.填表:直线的点斜式方程 4.做一做:直线l的点斜式方程是y-2=3(x+1),则直线l的斜率是( )
A.2 B.-1 C.3 D.-3
答案:C一二二、直线的斜截式方程
1.已知直线l的斜率为k,且与y轴的交点为(0,b),则直线l的方程是什么?
提示:将k及点(0,b)代入直线的点斜式方程得y=kx+b.
2.直线y=kx+b在y轴上的截距b是直线与y轴交点到原点的距离吗?它的取值范围是什么?
提示:不是直线与y轴交点到原点的距离,是直线y=kx+b在y轴上交点的纵坐标,截距b的取值范围是R.
3.一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么不同?
提示:一次函数的x的系数k≠0,否则就不是一次函数了;直线的斜截式方程y=kx+b中的k可以为0.一二4.填表:直线的斜截式方程 5.做一做:直线l的斜截式方程是y=-2x+3,则直线l在y轴上的截距为 .?
答案:3一二6.做一做:
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)直线y-3=m(x+1)恒过定点(-1,3).( )
(2)直线y=2x+3在y轴上的截距为3.( )
答案:(1)√ (2)√探究一探究二思维辨析直线的点斜式方程
例1 求满足下列条件的直线方程:
(1)经过点(2,-3),倾斜角是直线y= x倾斜角的2倍;
(2)经过点P(5,-2),且与y轴平行;
(3)过P(-2,3),Q(5,-4)两点.
思路分析:先求出直线的斜率,然后由点斜式写出方程.探究一探究二思维辨析(2)与y轴平行的直线,其斜率k不存在,不能用点斜式方程表示.
但直线上点的横坐标均为5,
故直线方程可记为x=5.∵直线过点P(-2,3),
∴由直线的点斜式方程可得直线方程为y-3=-(x+2),即x+y-1=0.探究一探究二思维辨析反思感悟点斜式方程的求法
(1)求直线的点斜式方程,关键是求出直线的斜率,所以,已知直线上一点的坐标及直线的斜率或直线上两点坐标,均可求出直线的方程.
(2) 斜率不存在时,可直接写出过点(x0,y0)的直线方程x=x0.探究一探究二思维辨析变式训练直线l1的倾斜角为135°,直线l2经过点B(-1,4).求满足下列条件的直线l2的方程.
(1)直线l2∥l1;
(2)直线l2⊥l1.
解:(1)由已知直线l1的斜率k1=tan 135°=-1.
因为l2∥l1,所以直线l2的斜率k2=k1=-1.
又直线l2经过点B(-1,4),
代入点斜式方程得y-4=-1×[x-(-1)],即y=-x+3.
(2)由已知直线l1的斜率k1=tan 135°=-1.又直线l2经过点B(-1,4),
代入点斜式方程得y-4=1×[x-(-1)],即y=x+5.探究一探究二思维辨析直线的斜截式方程
例2 求满足下列条件的直线方程:
(1)经过点(0,-2),且与直线y=3x-5垂直;
(2)与直线y=-2x+3平行,与直线y=4x-2在y轴上的截距相同.
思路分析:写出直线的斜率及在y轴上的截距,用斜截式写出直线方程.探究一探究二思维辨析解:(1)因为直线y=3x-5的斜率为3,且所求直线与该直线垂直,所以所求直线斜率为- .
又直线过点(0,-2),由直线方程的斜截式,得
y=- x-2,即x+3y+6=0.
(2)直线y=-2x+3的斜率为-2,直线y=4x-2在y轴上的截距为-2.
由题意知,所求直线的斜率为-2,在y轴上的截距也为-2.
由直线方程的斜截式,得y=-2x-2,
即2x+y+2=0.
反思感悟斜截式方程的求法
已知直线的斜率与y轴上的截距,可直接写出直线的方程;已知直线的斜截式方程,可得直线的斜率与y轴上的截距.直线的斜截式方程形式简单,特点明显,是运用较多的直线方程的形式之一.探究一探究二思维辨析延伸探究直线l与直线l1:y=2x+6在y轴上有相同的截距,且l的斜率与l1的斜率互为相反数,则直线l的方程为 .?
解析:由直线l1的方程可知它的斜率为2,它在y轴上的截距为6,所以直线l的斜率为-2,在y轴上的截距为6.由直线的斜截式方程可得直线l的方程为y=-2x+6.
答案:y=-2x+6探究一探究二思维辨析误把“截距”当“距离”致错
典例 已知斜率为- 的直线l与两坐标轴围成的三角形面积为6,求直线l的方程.探究一探究二思维辨析防范措施①用斜截式表示直线方程前提条件是斜率存在,不能用斜截式表示与x轴垂直的直线.②把直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距.注意“截距非距”,即截距不是距离,截距可以取一切实数,即可为正数、零或负数.当直线l与y轴的正半轴相交时,其在y轴上的截距b>0;当直线l与y轴的负半轴相交时,其在y轴上的截距b<0;当直线l经过原点时,其在y轴上的截距b=0.当直线l与y轴平行时,l在y轴上没有截距.1234答案:B 12342.与直线y=3x+1垂直,且过点(2,-1)的直线的斜截式方程是( ) 答案:B 12343.无论k取何值,直线y-2=k(x+1)所过的定点是 .?
答案:(-1,2)12344.直线l1与直线l2:y=3x+1平行,又直线l1过点(3,5),则直线l1的方程为 .?
解析:∵直线l2的斜率k2=3,l1与l2平行,
∴直线l1的斜率k1=3.
又直线l1过点(3,5),
∴l1的方程为y-5=3(x-3),即y=3x-4.
答案:y=3x-4
