3.3.2两点间的距离课件(21张)
文档属性
| 名称 | 3.3.2两点间的距离课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 741.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 15:50:03 | ||
图片预览








文档简介
课件21张PPT。3.3.2 两点间的距离两点间的距离
1. (1)在x轴上两点A1(x1,0),B1(x2,0)间的距离如何计算?
提示:|A1B1|=|x2-x1|.
(2)在y轴上两点C(0,y1),D(0,y2)间的距离如何计算?
提示:|CD|=|y2-y1|.
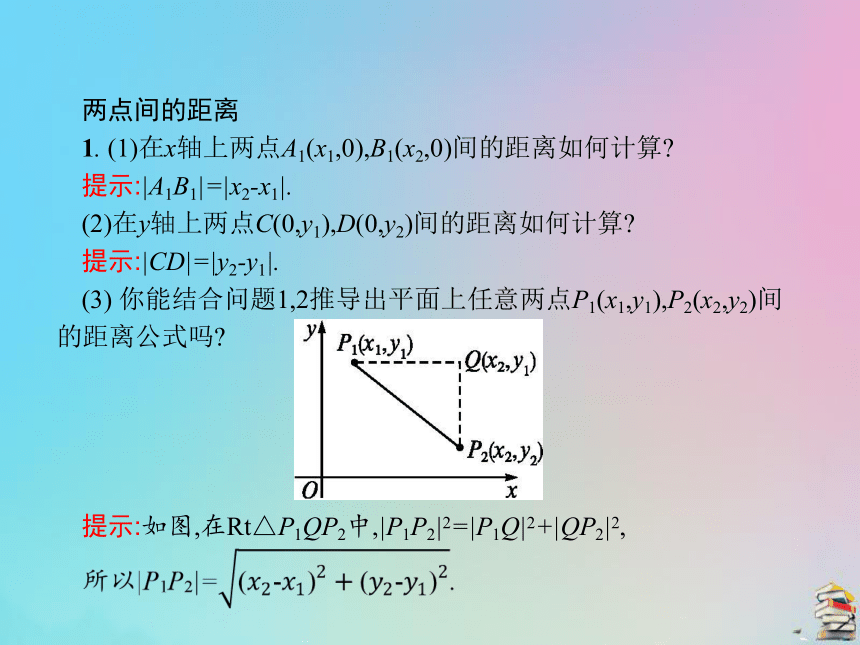
(3) 你能结合问题1,2推导出平面上任意两点P1(x1,y1),P2(x2,y2)间的距离公式吗?
提示:如图,在Rt△P1QP2中,|P1P2|2=|P1Q|2+|QP2|2,2.填空:
(1)平面上任意两点间的距离公式:平面上的两点P1(x1,y1),P2(x2,y2)
间的距离公式|P1P2|=(2)两点间距离的特殊情况: ②当P1P2∥x轴(y1=y2)时,|P1P2|=|x2-x1|.
③当P1P2∥y轴(x1=x2)时,|P1P2|=|y2-y1|.
3.做一做:已知点P1(4,2),P2(2,-2),则|P1P2|= .?探究一探究二探究三思想方法求两点间的距离
例1 已知△ABC三个顶点的坐标分别为A(-3,1),B(3,-3),C(1,7),试判断△ABC的形状.
思路分析:可求出三条边的长,根据所求长度判断三角形的形状.探究一探究二探究三思想方法∴|AB|=|AC|,且|AB|2+|AC|2=|BC|2.
∴△ABC是等腰直角三角形.∴|AC|=|AB|.∴△ABC是等腰直角三角形. 探究一探究二探究三思想方法反思感悟两点间距离公式的应用
两点间的距离公式是解析几何的重要公式之一,它主要解决线段的长度问题,体现了数形结合思想的应用.探究一探究二探究三思想方法延伸探究本例若改为:已知A(-1,-1),B(3,5),C(5,3),试判断△ABC的形状.探究一探究二探究三思想方法求点的坐标
例2 已知点A(-3,4),B(2, ),在x轴上找一点P,使|PA|=|PB|,并求|PA|的值.
思路分析:利用两点间的距离公式建立关于未知数的方程求解.
解:设点P(x,0),探究一探究二探究三思想方法反思感悟根据两点间的距离公式确定点的坐标
利用坐标平面内两点间的距离公式可以求平面上任意两个已知点间的距离.反过来,已知两点间的距离也可以根据条件求其中一个点的坐标.探究一探究二探究三思想方法变式训练 已知矩形ABCD相邻两个顶点A(-1,3),B(-2,4),若矩形对角线的交点在y轴上.求:另外两个顶点C和D的坐标.
解依题意可设矩形的两条对角线的交点为O(0,y),在矩形ABCD中,|AO|=|BO|,
解得y=5,交点O的坐标是(0,5),
∵A(-1,3),B(-2,4),设C(x1,y1),D(x2,y2),由于AC,BD中点均为O点,探究一探究二探究三思想方法坐标法的应用
例3 已知Rt△ABC,∠B为直角,AB=a,BC=b,建立适当的坐标系,写出顶点A,B,C的坐标,并求证斜边AC的中点M到三个顶点的距离相等.
思路分析:取直角边所在的直线为坐标轴建立坐标系,再写出各顶点坐标,给出证明.探究一探究二探究三思想方法解:取边BA所在的直线为x轴,边BC所在的直线为y轴,建立直角坐标系,如图所示,则三个顶点的坐标分别为A(a,0),B(0,0),C(0,b).由中点坐标公式,得斜边AC的中点M的坐标为 .∴|MA|=|MB|=|MC|. 探究一探究二探究三思想方法反思感悟坐标法及其应用
1.坐标法解决几何问题时,关键要结合图形的特征,建立平面直角坐标系.坐标系建立的是否合适,会直接影响问题能否方便解决.建系的原则主要有两点:
(1)让尽可能多的点落在坐标轴上,这样便于运算;
(2)如果条件中有互相垂直的两条线,要考虑将它们作为坐标轴;如果图形为中心对称图形,可考虑将中心作为原点;如果有轴对称性,可考虑将对称轴作为坐标轴.
2.利用坐标法解平面几何问题常见的步骤:
(1)建立坐标系,尽可能将有关元素放在坐标轴上;
(2)用坐标表示有关的量;
(3)将几何关系转化为坐标运算;
(4)把代数运算结果“翻译”成几何关系.探究一探究二探究三思想方法数形结合思想的典范——坐标法
典例 如图,在△ABC中,|AB|=|AC|,D是BC边上异于B,C的任意一点,求证:|AB|2=|AD|2+|BD|·|DC|.
【审题视角】建立适当的直角坐标系,设出各顶点的坐标,应用两点间的距离公式证明.探究一探究二探究三思想方法证明:如图,以BC的中点为原点O,BC所在的直线为x轴,建立直角坐标系.设A(0,a),B(-b,0),C(b,0),D(m,0)(-b则|AB|2=(-b-0)2+(0-a)2=a2+b2,
|AD|2=(m-0)2+(0-a)2=m2+a2,
|BD|·|DC|=|m+b|·|b-m|=(b+m)(b-m)=b2-m2,
∴|AD|2+|BD|·|DC|=a2+b2,
∴|AB|2=|AD|2+|BD|·|DC|.方法点睛根据图形的特点,建立适当的坐标系,可使运算量减小,因此要注意建系方法.探究一探究二探究三思想方法变式训练已知正三角形ABC的边长为a,在平面上求一点P,使|PA|2+|PB|2+|PC|2最小,并求此最小值.
解:以BC所在直线为x轴,以线段BC的中点为原点,建立直角坐标系,如图所示.
∵正三角形ABC的边长为a,12341.点A(1,-2)关于原点的对称点为A',则|AA'|为( )
解析:因为A(1,-2)关于原点的对称点A'(-1,2),所以
答案:A12342.以A(5,5),B(1,4),C(4,1)为顶点的三角形是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形故△ABC为等腰三角形.故选B.
答案:B12343.设点A在x轴上,点B在y轴上,线段AB的中点P(2,-1),则|AB|=( )解析:依题意设A(a,0),B(0,b),
∵P(2,-1)为线段AB的中点,
∴a=4,b=-2.∴A(4,0),B(0,-2).答案:A 12344.直线y=x+2被坐标轴截得的线段长为 .?
解析:令x=0,得y=2;令y=0,得x=-2,则点(0,2)和点(-2,0)间的距离为
1. (1)在x轴上两点A1(x1,0),B1(x2,0)间的距离如何计算?
提示:|A1B1|=|x2-x1|.
(2)在y轴上两点C(0,y1),D(0,y2)间的距离如何计算?
提示:|CD|=|y2-y1|.
(3) 你能结合问题1,2推导出平面上任意两点P1(x1,y1),P2(x2,y2)间的距离公式吗?
提示:如图,在Rt△P1QP2中,|P1P2|2=|P1Q|2+|QP2|2,2.填空:
(1)平面上任意两点间的距离公式:平面上的两点P1(x1,y1),P2(x2,y2)
间的距离公式|P1P2|=(2)两点间距离的特殊情况: ②当P1P2∥x轴(y1=y2)时,|P1P2|=|x2-x1|.
③当P1P2∥y轴(x1=x2)时,|P1P2|=|y2-y1|.
3.做一做:已知点P1(4,2),P2(2,-2),则|P1P2|= .?探究一探究二探究三思想方法求两点间的距离
例1 已知△ABC三个顶点的坐标分别为A(-3,1),B(3,-3),C(1,7),试判断△ABC的形状.
思路分析:可求出三条边的长,根据所求长度判断三角形的形状.探究一探究二探究三思想方法∴|AB|=|AC|,且|AB|2+|AC|2=|BC|2.
∴△ABC是等腰直角三角形.∴|AC|=|AB|.∴△ABC是等腰直角三角形. 探究一探究二探究三思想方法反思感悟两点间距离公式的应用
两点间的距离公式是解析几何的重要公式之一,它主要解决线段的长度问题,体现了数形结合思想的应用.探究一探究二探究三思想方法延伸探究本例若改为:已知A(-1,-1),B(3,5),C(5,3),试判断△ABC的形状.探究一探究二探究三思想方法求点的坐标
例2 已知点A(-3,4),B(2, ),在x轴上找一点P,使|PA|=|PB|,并求|PA|的值.
思路分析:利用两点间的距离公式建立关于未知数的方程求解.
解:设点P(x,0),探究一探究二探究三思想方法反思感悟根据两点间的距离公式确定点的坐标
利用坐标平面内两点间的距离公式可以求平面上任意两个已知点间的距离.反过来,已知两点间的距离也可以根据条件求其中一个点的坐标.探究一探究二探究三思想方法变式训练 已知矩形ABCD相邻两个顶点A(-1,3),B(-2,4),若矩形对角线的交点在y轴上.求:另外两个顶点C和D的坐标.
解依题意可设矩形的两条对角线的交点为O(0,y),在矩形ABCD中,|AO|=|BO|,
解得y=5,交点O的坐标是(0,5),
∵A(-1,3),B(-2,4),设C(x1,y1),D(x2,y2),由于AC,BD中点均为O点,探究一探究二探究三思想方法坐标法的应用
例3 已知Rt△ABC,∠B为直角,AB=a,BC=b,建立适当的坐标系,写出顶点A,B,C的坐标,并求证斜边AC的中点M到三个顶点的距离相等.
思路分析:取直角边所在的直线为坐标轴建立坐标系,再写出各顶点坐标,给出证明.探究一探究二探究三思想方法解:取边BA所在的直线为x轴,边BC所在的直线为y轴,建立直角坐标系,如图所示,则三个顶点的坐标分别为A(a,0),B(0,0),C(0,b).由中点坐标公式,得斜边AC的中点M的坐标为 .∴|MA|=|MB|=|MC|. 探究一探究二探究三思想方法反思感悟坐标法及其应用
1.坐标法解决几何问题时,关键要结合图形的特征,建立平面直角坐标系.坐标系建立的是否合适,会直接影响问题能否方便解决.建系的原则主要有两点:
(1)让尽可能多的点落在坐标轴上,这样便于运算;
(2)如果条件中有互相垂直的两条线,要考虑将它们作为坐标轴;如果图形为中心对称图形,可考虑将中心作为原点;如果有轴对称性,可考虑将对称轴作为坐标轴.
2.利用坐标法解平面几何问题常见的步骤:
(1)建立坐标系,尽可能将有关元素放在坐标轴上;
(2)用坐标表示有关的量;
(3)将几何关系转化为坐标运算;
(4)把代数运算结果“翻译”成几何关系.探究一探究二探究三思想方法数形结合思想的典范——坐标法
典例 如图,在△ABC中,|AB|=|AC|,D是BC边上异于B,C的任意一点,求证:|AB|2=|AD|2+|BD|·|DC|.
【审题视角】建立适当的直角坐标系,设出各顶点的坐标,应用两点间的距离公式证明.探究一探究二探究三思想方法证明:如图,以BC的中点为原点O,BC所在的直线为x轴,建立直角坐标系.设A(0,a),B(-b,0),C(b,0),D(m,0)(-b
|AD|2=(m-0)2+(0-a)2=m2+a2,
|BD|·|DC|=|m+b|·|b-m|=(b+m)(b-m)=b2-m2,
∴|AD|2+|BD|·|DC|=a2+b2,
∴|AB|2=|AD|2+|BD|·|DC|.方法点睛根据图形的特点,建立适当的坐标系,可使运算量减小,因此要注意建系方法.探究一探究二探究三思想方法变式训练已知正三角形ABC的边长为a,在平面上求一点P,使|PA|2+|PB|2+|PC|2最小,并求此最小值.
解:以BC所在直线为x轴,以线段BC的中点为原点,建立直角坐标系,如图所示.
∵正三角形ABC的边长为a,12341.点A(1,-2)关于原点的对称点为A',则|AA'|为( )
解析:因为A(1,-2)关于原点的对称点A'(-1,2),所以
答案:A12342.以A(5,5),B(1,4),C(4,1)为顶点的三角形是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形故△ABC为等腰三角形.故选B.
答案:B12343.设点A在x轴上,点B在y轴上,线段AB的中点P(2,-1),则|AB|=( )解析:依题意设A(a,0),B(0,b),
∵P(2,-1)为线段AB的中点,
∴a=4,b=-2.∴A(4,0),B(0,-2).答案:A 12344.直线y=x+2被坐标轴截得的线段长为 .?
解析:令x=0,得y=2;令y=0,得x=-2,则点(0,2)和点(-2,0)间的距离为
