江苏省苏州市2008-2018学年高二(下)期末数学试卷(理科)分类汇编:空间向量
文档属性
| 名称 | 江苏省苏州市2008-2018学年高二(下)期末数学试卷(理科)分类汇编:空间向量 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 15:56:25 | ||
图片预览




文档简介
空间向量
(苏州市2008-2009高二 理(下)期末)16. 在正方体中,为棱的中点。
求证:;
求与平面所成角的正弦值.
(苏州市2009-2010高二 理(下)期末)4.?已知向量a=(2,,x),b=(x,1,2),其中,若a∥b,则x= .
(苏州市2009-2010高二 理(下)期末)16.?(本小题满分14分)如图,在三棱锥C-OAB中,OA⊥OB,CB⊥平面OAB,?OA=2,?OB=4,?BC=6,M为AC的中点,求:
直线OM与AB所成角的余弦值;
直线AB与平面OAC所成角的正弦值.
(苏州市2010-2011高二 理(下)期末)4.在空间直角坐标系中,点P(4,3,7)关于平面 xOz的对称点P’的坐标为 .
(苏州市2010-2011高二 理(下)期末)17.(本小题满分14分)已知菱形ABCD的边长为6,∠BAD=600,AC∩BD=O.将菱形ABCD沿对角线AC折起,使∠BOD=90?.
如图所示建立空间直角坐标系,设点N(0,y,z)是线段BD上一个动点.
①写出y与z的关系,并指出y的取值范围;
②若CN=,试确定N的位置.
(2)求二面角A-BD-O大小的余弦值.
(苏州市2011-2012高二 理(下)期末)3.空间直角坐标系中,点P(1,2,2)到原点O的距离为 .
(苏州市2011-2012高二 理(下)期末)17.(本小题满分14分)在如图所示的空间直角坐标系中,正方体ABCD A1B1C1D1的棱长为2,E、F分别为A1D1和A1B1的中点.
求异面直线AE和BF所成的角的余弦值;
求平面B1BDD1与平面BFC1所成的锐二面角的余弦值;
若点P在正方形ABCD内部或其边界上,且EP∥平面BFC1,求EP的最大值和最小值.
(苏州市2012-2013高二 理(下)期末)17.(本小题满分14分)如图,在长方体ABCD A1B1C1D1中,AB = 4,AD = 2,A1A = 2,点F是棱BC的中点,点E在棱C1D1上,且D1E = λ EC1(λ为实数).
求二面角D1 AC D的余弦值;
当λ =时,求直线EF与平面D1AC所成角的正弦值的大小;
求证:直线与直线不可能垂直.
(苏州市2013-2014高二 理(下)期末)3.空间直角坐标系中,点A(1,2,3),点B(1,3,-1),则AB= .
(苏州市2014-2015高二 理(下)期末)18.(本小题满分16 分)在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,AB=AF=2EF=1,点P在棱DF上.
若点P是DF的中点,求异面直线BE与CP所成角的余弦值;
若二面角D ? AP ? C 的余弦值为,求PF的长度.
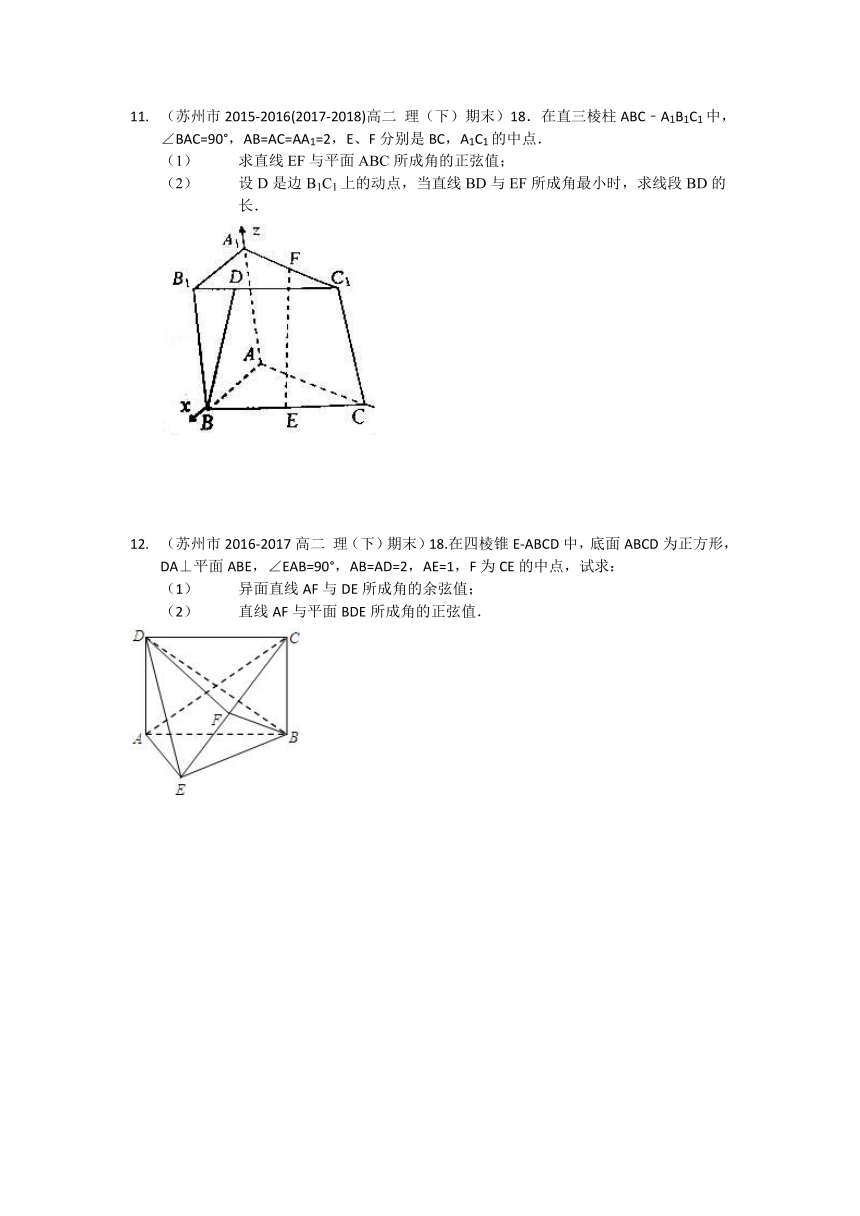
(苏州市2015-2016(2017-2018)高二 理(下)期末)18.在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E、F分别是BC,A1C1的中点.
求直线EF与平面ABC所成角的正弦值;
设D是边B1C1上的动点,当直线BD与EF所成角最小时,求线段BD的长.
(苏州市2016-2017高二 理(下)期末)18.在四棱锥E-ABCD中,底面ABCD为正方形,DA⊥平面ABE,∠EAB=90°,AB=AD=2,AE=1,F为CE的中点,试求:
异面直线AF与DE所成角的余弦值;
直线AF与平面BDE所成角的正弦值.
答案:
解:如图建立空间直角坐标系
设正方体的棱长为2,则A(2,0,0),B(2,2,0),C(0,2,0),E(0,2,1),D1(0,0,2),B1(2,2,2)
所以 =(2,2,0), =(-2,2,1)
∵ ? =0
∴ ⊥
∴D1B1⊥AE
求出(2)设平面ABE的法向量 =(a,b,1)
∵ =(0,2,0), =(-2,2,1)
∴
解得a= ,b=0, =(,0,1)
∴sinθ==
x=
解:(1)建立如图所示的坐标系,有O(0,0,0),A(2,0,0),
B(0,4,0),C(0,4,6),M(1,2,3)
∴,
∴=-2+8+0=6
∴cos<>==
(2)设平面OAC的法向量为,
则,
∴2a=0,
4b+6c=0,
∴
设直线AB与平面OAC所成的角是θ,
∴sinθ=|cos<>=
(4,3,7)
(1)①设N(0,y,z),,
则(0,y,z-3)=λ(0,3,-3),
所以y=3λ,z=3-3λ,
∴y+z=3(0y3)
②N(0,3λ,3-3λ),,
由得,即9λ2-9λ+2=0,
解得或,
所以N点的坐标为(0,2,1)或(0,1,2)
(也可以答是线段BD的三等分点,或)
(2)由题意,OB=OD=3,
因为,
所以∠BOD=90°,OB⊥OD
又因为菱形ABCD,所以OB⊥AC,OD⊥AC.
.,B(0,0,3).
所以,
设平面ABD的法向量为n=(x,y,z),
则有即:
令x=1,则,所以n=
因为AC⊥OB,AC⊥OD,所以AC⊥平面BOD.
平面BOD的法向量与AC平行,
所以平面BOD的法向量为n0=(1,0,0)
∴,
因为二面角A-BD-O是锐角,
所以二面角A-BD-O的余弦值为.
3
17.解:(1)A(2,0,0),E(1,0,2),
B(2,2,0),F(2,1,2).
∴,
. …………………… 2分
则.
∴异面直线AE和BF所成的角的余弦值为. …………………… 4分
(2)平面B1BDD1的一个法向量,…………………… 5分
设平面BFC1的法向量为,
∴
取得平面BFC1的一个法向量. ………………… 7分
. ………………… 8分
∴平面B1BDD1与平面BFC1所成的锐二面角的余弦值为.…………… 9分
(3)设P(x,y,0)(0≤x≤2,0≤y≤2), …………… 10分
则.
由,得,即x 2y 3 0. …………… 11分
∵0≤x≤2,∴0≤3 2y≤2.则. …………… 12分
∵,
∴当时,EP取得最小值为;
当时,EP取得最大值为. …………… 14分
17.解:(1)如图所示,建立空间直角坐标系.
则
,. ………… 2分
设平面的法向量为,
则.
即.令,则.
∴平面的一个法向量.…… 4分
又平面的一个法向量为.
故,
即二面角的余弦值为. ……… 6分
(2)当λ =时,E(0,1,2),F(1,4,0),.
所以. ……………9分
因为 ,所以为锐角,
从而直线EF与平面所成角的正弦值的大小为. ……………10分
(3)假设,则.
∵,
∴,. ……………12分
∴.化简得.
该方程无解,所以假设不成立,即直线不可能与直线不可能垂直.……14分
因为∠BAF=90°,所以AF⊥AB,
因为平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,所以AF⊥平面ABCD,
因为四边形ABCD为矩形,所以以A为坐标原点,AB,AD,AF分别为x,y,z轴,建立如图所示空间直角坐标系O-xyz.
所以B(1,0,0),E(,0,1),P(0,1,),C(1,2,0).
所以=(-,0,1),=(-1,-1,),
所以cos<,>==,
即异面直线BE与CP所成角的余弦值为.…(9分)
(Ⅱ)因为AB⊥平面ADF,所以平面APF的法向量为n1=(1,0,0)
设P点坐标为(0,2-2t,t),在平面APC中,==(0,2-2t,t),
=(1,2,0),所以平面APC的法向量为n2=(-2,1,),
所以cos<n1,n2>==,
解得t=,或t=2(舍).
此时|PF|=.…(14分)
解:(1)取AC的中点M,连结FM,EM.
∵F,M分别是A1C1,AC的中点,四边形ACC1A1是矩形,
∴FM∥AA1,FM=AA1=2,
∵AA1∥平面ABC,
∴FM⊥平面ABC,
∴∠FEM是EF与平面ABC所成的角.
∵E,M分别是BC,AC的中点,
∴EM==1.∴EF==.
∴sin∠FEM==.
∴直线EF与平面ABC所成角的正弦值为.
(2)以A为原点,以AB,AC,AA1为坐标轴建立空间直角坐标系,如图所示:
则B(2,0,0),E(1,1,0),F(0,1,2).B1(2,0,2),C1(0,2,2).
∴=(﹣1,0,2),=(0,0,2),=(﹣2,2,0),
设=λ=(﹣2λ,2λ,0),则=+=(﹣2λ,2λ,2).(0≤λ≤1)
∴=2λ+4.
∴cos<>===.
∴当即λ=时,cos<>取得最大值,即直线BD与EF所成角最小.
此时, =(﹣,,2),∴|BD|=||=.
(苏州市2008-2009高二 理(下)期末)16. 在正方体中,为棱的中点。
求证:;
求与平面所成角的正弦值.
(苏州市2009-2010高二 理(下)期末)4.?已知向量a=(2,,x),b=(x,1,2),其中,若a∥b,则x= .
(苏州市2009-2010高二 理(下)期末)16.?(本小题满分14分)如图,在三棱锥C-OAB中,OA⊥OB,CB⊥平面OAB,?OA=2,?OB=4,?BC=6,M为AC的中点,求:
直线OM与AB所成角的余弦值;
直线AB与平面OAC所成角的正弦值.
(苏州市2010-2011高二 理(下)期末)4.在空间直角坐标系中,点P(4,3,7)关于平面 xOz的对称点P’的坐标为 .
(苏州市2010-2011高二 理(下)期末)17.(本小题满分14分)已知菱形ABCD的边长为6,∠BAD=600,AC∩BD=O.将菱形ABCD沿对角线AC折起,使∠BOD=90?.
如图所示建立空间直角坐标系,设点N(0,y,z)是线段BD上一个动点.
①写出y与z的关系,并指出y的取值范围;
②若CN=,试确定N的位置.
(2)求二面角A-BD-O大小的余弦值.
(苏州市2011-2012高二 理(下)期末)3.空间直角坐标系中,点P(1,2,2)到原点O的距离为 .
(苏州市2011-2012高二 理(下)期末)17.(本小题满分14分)在如图所示的空间直角坐标系中,正方体ABCD A1B1C1D1的棱长为2,E、F分别为A1D1和A1B1的中点.
求异面直线AE和BF所成的角的余弦值;
求平面B1BDD1与平面BFC1所成的锐二面角的余弦值;
若点P在正方形ABCD内部或其边界上,且EP∥平面BFC1,求EP的最大值和最小值.
(苏州市2012-2013高二 理(下)期末)17.(本小题满分14分)如图,在长方体ABCD A1B1C1D1中,AB = 4,AD = 2,A1A = 2,点F是棱BC的中点,点E在棱C1D1上,且D1E = λ EC1(λ为实数).
求二面角D1 AC D的余弦值;
当λ =时,求直线EF与平面D1AC所成角的正弦值的大小;
求证:直线与直线不可能垂直.
(苏州市2013-2014高二 理(下)期末)3.空间直角坐标系中,点A(1,2,3),点B(1,3,-1),则AB= .
(苏州市2014-2015高二 理(下)期末)18.(本小题满分16 分)在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,AB=AF=2EF=1,点P在棱DF上.
若点P是DF的中点,求异面直线BE与CP所成角的余弦值;
若二面角D ? AP ? C 的余弦值为,求PF的长度.
(苏州市2015-2016(2017-2018)高二 理(下)期末)18.在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E、F分别是BC,A1C1的中点.
求直线EF与平面ABC所成角的正弦值;
设D是边B1C1上的动点,当直线BD与EF所成角最小时,求线段BD的长.
(苏州市2016-2017高二 理(下)期末)18.在四棱锥E-ABCD中,底面ABCD为正方形,DA⊥平面ABE,∠EAB=90°,AB=AD=2,AE=1,F为CE的中点,试求:
异面直线AF与DE所成角的余弦值;
直线AF与平面BDE所成角的正弦值.
答案:
解:如图建立空间直角坐标系
设正方体的棱长为2,则A(2,0,0),B(2,2,0),C(0,2,0),E(0,2,1),D1(0,0,2),B1(2,2,2)
所以 =(2,2,0), =(-2,2,1)
∵ ? =0
∴ ⊥
∴D1B1⊥AE
求出(2)设平面ABE的法向量 =(a,b,1)
∵ =(0,2,0), =(-2,2,1)
∴
解得a= ,b=0, =(,0,1)
∴sinθ==
x=
解:(1)建立如图所示的坐标系,有O(0,0,0),A(2,0,0),
B(0,4,0),C(0,4,6),M(1,2,3)
∴,
∴=-2+8+0=6
∴cos<>==
(2)设平面OAC的法向量为,
则,
∴2a=0,
4b+6c=0,
∴
设直线AB与平面OAC所成的角是θ,
∴sinθ=|cos<>=
(4,3,7)
(1)①设N(0,y,z),,
则(0,y,z-3)=λ(0,3,-3),
所以y=3λ,z=3-3λ,
∴y+z=3(0y3)
②N(0,3λ,3-3λ),,
由得,即9λ2-9λ+2=0,
解得或,
所以N点的坐标为(0,2,1)或(0,1,2)
(也可以答是线段BD的三等分点,或)
(2)由题意,OB=OD=3,
因为,
所以∠BOD=90°,OB⊥OD
又因为菱形ABCD,所以OB⊥AC,OD⊥AC.
.,B(0,0,3).
所以,
设平面ABD的法向量为n=(x,y,z),
则有即:
令x=1,则,所以n=
因为AC⊥OB,AC⊥OD,所以AC⊥平面BOD.
平面BOD的法向量与AC平行,
所以平面BOD的法向量为n0=(1,0,0)
∴,
因为二面角A-BD-O是锐角,
所以二面角A-BD-O的余弦值为.
3
17.解:(1)A(2,0,0),E(1,0,2),
B(2,2,0),F(2,1,2).
∴,
. …………………… 2分
则.
∴异面直线AE和BF所成的角的余弦值为. …………………… 4分
(2)平面B1BDD1的一个法向量,…………………… 5分
设平面BFC1的法向量为,
∴
取得平面BFC1的一个法向量. ………………… 7分
. ………………… 8分
∴平面B1BDD1与平面BFC1所成的锐二面角的余弦值为.…………… 9分
(3)设P(x,y,0)(0≤x≤2,0≤y≤2), …………… 10分
则.
由,得,即x 2y 3 0. …………… 11分
∵0≤x≤2,∴0≤3 2y≤2.则. …………… 12分
∵,
∴当时,EP取得最小值为;
当时,EP取得最大值为. …………… 14分
17.解:(1)如图所示,建立空间直角坐标系.
则
,. ………… 2分
设平面的法向量为,
则.
即.令,则.
∴平面的一个法向量.…… 4分
又平面的一个法向量为.
故,
即二面角的余弦值为. ……… 6分
(2)当λ =时,E(0,1,2),F(1,4,0),.
所以. ……………9分
因为 ,所以为锐角,
从而直线EF与平面所成角的正弦值的大小为. ……………10分
(3)假设,则.
∵,
∴,. ……………12分
∴.化简得.
该方程无解,所以假设不成立,即直线不可能与直线不可能垂直.……14分
因为∠BAF=90°,所以AF⊥AB,
因为平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,所以AF⊥平面ABCD,
因为四边形ABCD为矩形,所以以A为坐标原点,AB,AD,AF分别为x,y,z轴,建立如图所示空间直角坐标系O-xyz.
所以B(1,0,0),E(,0,1),P(0,1,),C(1,2,0).
所以=(-,0,1),=(-1,-1,),
所以cos<,>==,
即异面直线BE与CP所成角的余弦值为.…(9分)
(Ⅱ)因为AB⊥平面ADF,所以平面APF的法向量为n1=(1,0,0)
设P点坐标为(0,2-2t,t),在平面APC中,==(0,2-2t,t),
=(1,2,0),所以平面APC的法向量为n2=(-2,1,),
所以cos<n1,n2>==,
解得t=,或t=2(舍).
此时|PF|=.…(14分)
解:(1)取AC的中点M,连结FM,EM.
∵F,M分别是A1C1,AC的中点,四边形ACC1A1是矩形,
∴FM∥AA1,FM=AA1=2,
∵AA1∥平面ABC,
∴FM⊥平面ABC,
∴∠FEM是EF与平面ABC所成的角.
∵E,M分别是BC,AC的中点,
∴EM==1.∴EF==.
∴sin∠FEM==.
∴直线EF与平面ABC所成角的正弦值为.
(2)以A为原点,以AB,AC,AA1为坐标轴建立空间直角坐标系,如图所示:
则B(2,0,0),E(1,1,0),F(0,1,2).B1(2,0,2),C1(0,2,2).
∴=(﹣1,0,2),=(0,0,2),=(﹣2,2,0),
设=λ=(﹣2λ,2λ,0),则=+=(﹣2λ,2λ,2).(0≤λ≤1)
∴=2λ+4.
∴cos<>===.
∴当即λ=时,cos<>取得最大值,即直线BD与EF所成角最小.
此时, =(﹣,,2),∴|BD|=||=.
