江苏省苏州市2008-2018学年高二(下)期末数学试卷(理科)分类汇编:立体几何
文档属性
| 名称 | 江苏省苏州市2008-2018学年高二(下)期末数学试卷(理科)分类汇编:立体几何 |
|
|
| 格式 | zip | ||
| 文件大小 | 674.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 00:00:00 | ||
图片预览


文档简介
立体几何
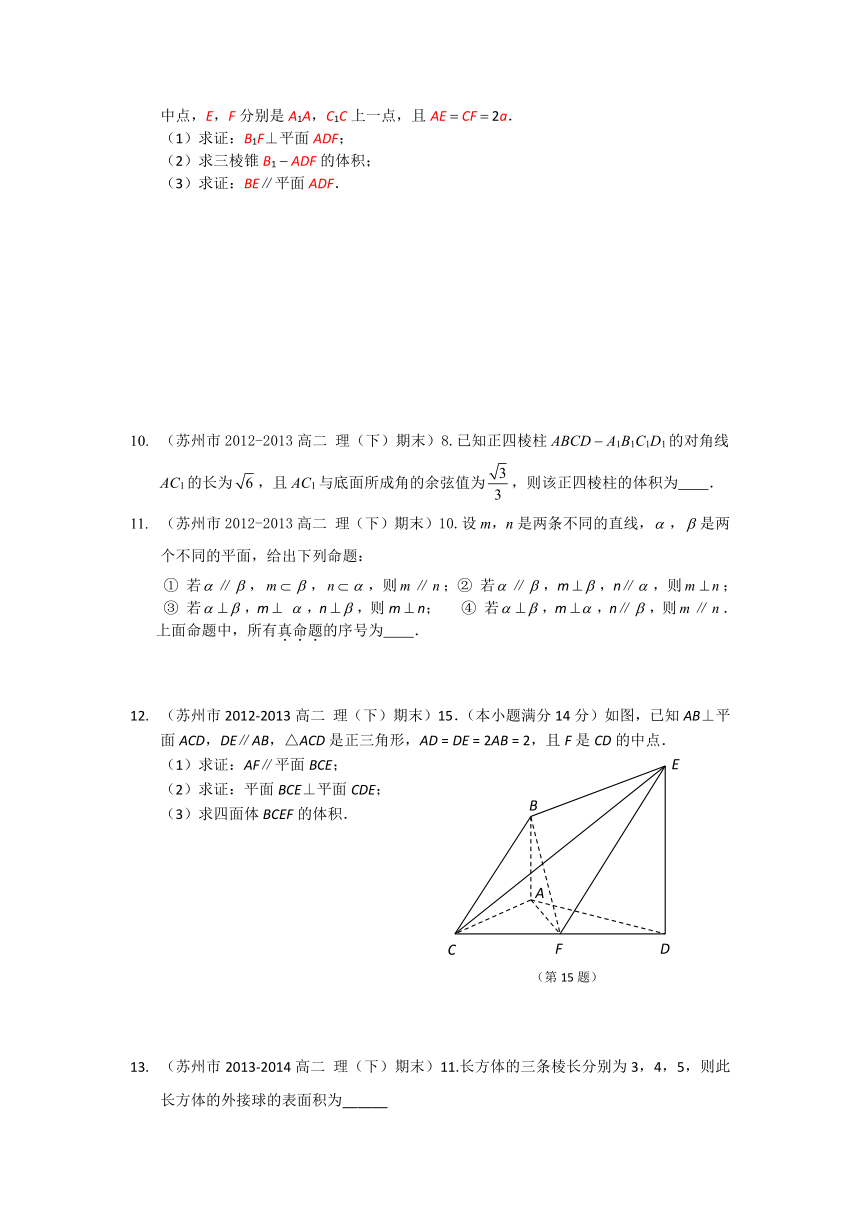
(苏州市2008-2009高二 理(下)期末)6. 设是球表面上的四个点,两两垂直,且,则求的表面积= 。
(苏州市2008-2009高二 理(下)期末)11. 在正四面体中,分别是棱的中点。
给出下面四个结论:①;②;③;④,其中所有不正确的结论的序号是 。
(苏州市2008-2009高二 理(下)期末)18. 如图,在矩形中,已知,为的中点,现将折起,使点A到点P处,满足PB=PC,设M,H分别为PC,DE的中点。
(1)求证:;
(2)线段上是否存在一点,使?试证明你的结论;
(3)求的面积.
(苏州市2009-2010高二 理(下)期末)8.?棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,
给出下列命题:
????①直线MN∥平面ABC;
????②直线CD⊥平面BMN;
③三棱锥B-AMN的体积是三棱锥B-ACM的体积的一半.
则其中正确命题的序号为????? ?????.
(苏州市2009-2010高二 理(下)期末)17.(本小题满分14分)在斜三棱柱ABC-A1B1C1中,BB1=BA=BC=1,∠B1BC=60°,∠ABC=90°,平面BB1C1C⊥平面ABC,??M、N分别是BC的三等分点.
(1)求证:A1N∥平面AB1M;?
(2)求证:AB⊥B1M;?
(3)求三棱锥A-B1BC的体积V.
(苏州市2010-2011高二 理(下)期末)10.底面边长为2,高为1的正三棱锥的全面积为 .
(苏州市2010-2011高二 理(下)期末)16.(本小题满分14分)如图,已知四边形ABCD是矩形,AD⊥平面ABE,AD=AE,点F在线段DE上,且AF⊥平面BDE.求证:
(1)BE⊥平面ADE;
(2)BE∥平面AFC;
(3)平面AFC⊥平面ADE.
(苏州市2011-2012高二 理(下)期末)10.如图,在四棱锥P ABCD中,已知底面ABCD是矩形,AB 2,AD a,PD⊥平面ABCD,若边AB上存在点M,使得PM⊥CM,则实数a 的取值范围是 .
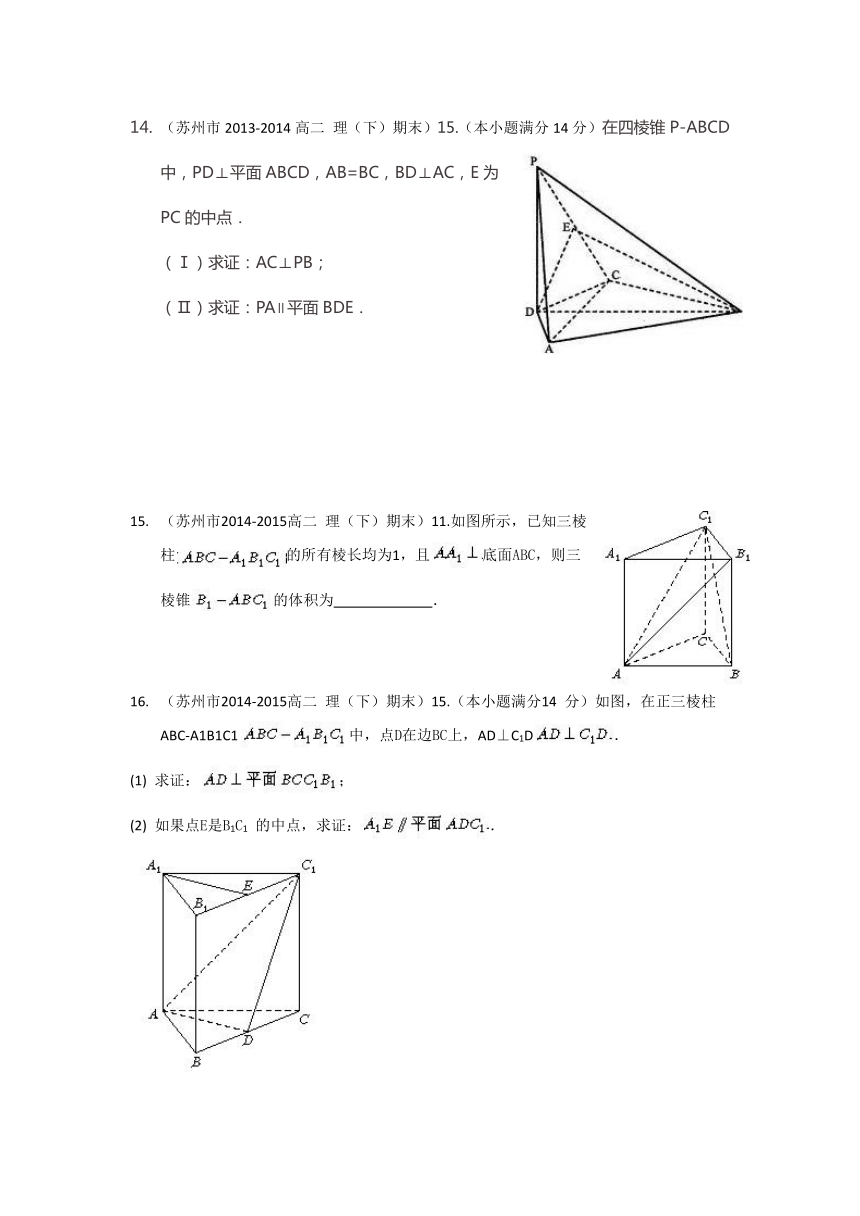
(苏州市2011-2012高二 理(下)期末)15.(本小题满分14分)在直三棱柱ABC A1B1C1中,AB AC AA1 3a,BC 2a,D是BC的中点,E,F分别是A1A,C1C上一点,且AE CF 2a.
(1)求证:B1F⊥平面ADF;
(2)求三棱锥B1 ADF的体积;
(3)求证:BE∥平面ADF.
(苏州市2012-2013高二 理(下)期末)8.已知正四棱柱ABCD A1B1C1D1的对角线AC1的长为,且AC1与底面所成角的余弦值为,则该正四棱柱的体积为 .
(苏州市2012-2013高二 理(下)期末)10.设m,n是两条不同的直线,,是两个不同的平面,给出下列命题:
① 若∥,,,则∥;② 若∥,m ,n∥,则;
③ 若,m ,n ,则m n; ④ 若,m ,n∥,则∥.
上面命题中,所有真命题的序号为 .
(苏州市2012-2013高二 理(下)期末)15.(本小题满分14分)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD = DE = 2AB = 2,且F是CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求四面体BCEF的体积.
(苏州市2013-2014高二 理(下)期末)11.长方体的三条棱长分别为3,4,5,则此长方体的外接球的表面积为______
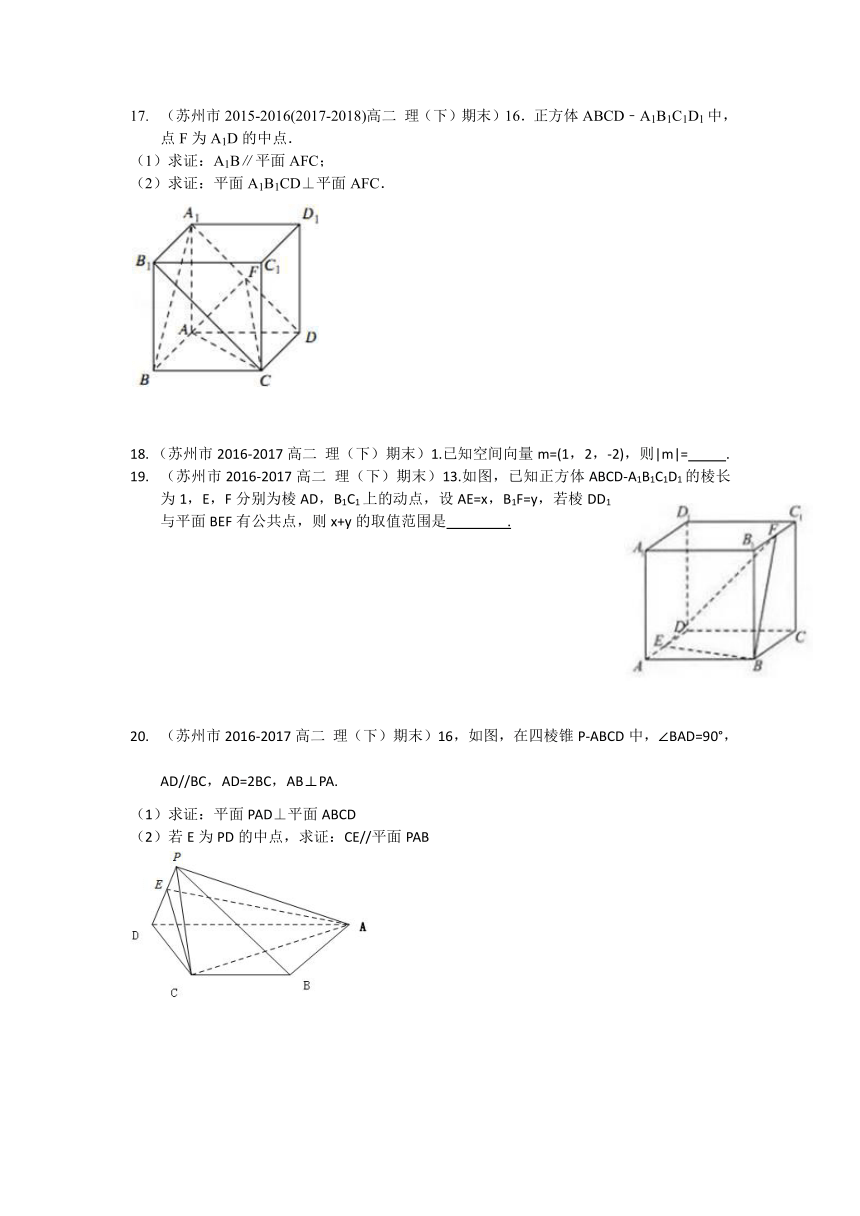
(苏州市2013-2014高二 理(下)期末)15.(本小题满分14分)在四棱锥P-ABCD中,PD⊥平面ABCD,AB=BC,BD⊥AC,E为PC的中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PA∥平面BDE.
(苏州市2014-2015高二 理(下)期末)11.如图所示,已知三棱柱的所有棱长均为1,且底面ABC,则三棱锥的体积为 .
(苏州市2014-2015高二 理(下)期末)15.(本小题满分14 分)如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
(1) 求证:;
(2) 如果点E是B1C1 的中点,求证:.
(苏州市2015-2016(2017-2018)高二 理(下)期末)16.正方体ABCD﹣A1B1C1D1中,点F为A1D的中点.
(1)求证:A1B∥平面AFC;
(2)求证:平面A1B1CD⊥平面AFC.
(苏州市2016-2017高二 理(下)期末)1.已知空间向量m=(1,2,-2),则|m|= .
(苏州市2016-2017高二 理(下)期末)13.如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是 .
(苏州市2016-2017高二 理(下)期末)16,如图,在四棱锥P-ABCD中,∠BAD=90°,AD//BC,AD=2BC,AB⊥PA.
(1)求证:平面PAD⊥平面ABCD
(2)若E为PD的中点,求证:CE//平面PAB
答案:
立体几何
3π
证明:(1)取PD的中点F,连接EF,FM
由条件知:FM平行且等于DC的一半,EB平行且等于DC的一半
∴FM∥EB,且FM=EB
则四边形EFMB是平行四边形
则BM∥EF
∵BM?平面PDE,EF?平面PDE
∴BM∥平面PDE;
当N为BC的中点时,BC⊥平面PHN,理由如下:
由题意得,HN为直角梯形BCDE的中位线
∴HN⊥BC
∵PB=PC
∴PN⊥BC
又∵HN∩PN=N
∴BC⊥平面PHN,
由(2)中结论可得,BC⊥PH,
又∵PH⊥DE
故PH⊥底面BCDE
则PH⊥HN,即△PHN为直角三角形
∵AB=2AD=4,E为AB的中点
∴BC=2,HN=3,PH= ,则PN=
∴△PBC的面积S= ?BC?PN=
解(1)连A1B交AB1与O,连OM,
则OM为△A1BN的中位线
∴OM∥A1N
∵A1N?平面AB1M,OM?平面AB1M
∴A1N∥平面AB1M.
(2)∵平面BB1C1C⊥平面ABC,而∠ABC=90°
∴AB⊥BC,AB?平面ABC
∴AB⊥平面BB1C1C
∵B1M?平面BB1C1C
∴AB⊥B1M.
(3)∵AB⊥平面BB1C1C
∴V=×(×1×1×sin600)×1=
3
(1)∵AF⊥平面BDE,BE?平面BDE,AD⊥平面ABE,BE?平面ABE
∴AF⊥BE,AD⊥BE,而AD∩AF=A
∴BE⊥平面ADE;
(2)设AC与BD交于O,连接FO
∵AD=AE,AF⊥DE
∴点F为DE的中点,而O为BD的中点
根据中位线定理可知BE∥FO
而FO?平面AFC,BE?平面AFC
∴BE∥平面AFC;
(3)∵BE⊥平面ADE,BE∥FO
∴FO⊥平面ADE
而FO?平面AFC
∴平面AFC⊥平面ADE.
(0,1]
证明:∵AB AC,D为BC中点,
∴AD⊥BC. …………… 1分
在直三棱柱ABC A1B1C1中,
∵B1B⊥底面ABC,AD底面ABC,
∴AD⊥B1B. …………… 2分
∵BCB1B B,∴AD⊥平面B1BCC1.…………… 3分
∵B1F平面B1BCC1,∴AD⊥B1F. …………… 4分
在矩形B1BCC1中,
∵C1F CD a,B1C1 CF 2a,
∴Rt△DCF ≌ Rt△FC1B1.
∴?CFD ?C1B1F.∴?B1FD 90°.
∴B1F⊥FD. …………………… 5分
∵ADFD D,∴B1F⊥平面AFD. …………… 6分
(2)∵B1F⊥平面AFD,
∴
=. ……………… 10分
(3)连EF,EC,设,连,
,∴四边形AEFC为矩形,为中点.
为中点,. ……………… 12分
平面,平面,
平面. ……………… 14分
2
②
15.证明:(1)取EC中点G,连BG,GF.
∵F是CD的中点,∴FG∥DE,且FG =DE.
又∵AB∥DE,且AB =DE.
∴四边形ABGF为平行四边形.……… 3分
∴AF∥BG.又BG平面BCE,AF平面BCE.
(条件每少一个扣1分,最多扣2分)
∴AF∥平面BCE. …………5分
(2)∵AB 平面ACD,AF平面ACD,
∴AB AF.∵AB∥DE,∴AF DE. ………… 6分
又∵△ACD为正三角形,∴AF CD. ………… 7分
∵BG∥AF,∴BG DE,BG CD. ………… 8分
∵CD ∩ DE = D,∴BG 平面CDE. ………… 9分
(直接用AF∥BG,AF平面CDE,而得到BG 平面CDE.扣1分)
∵BG平面BCE,∴平面BCE⊥平面CDE; ……………11分
(3)四面体BCEF的体积
. ……………14分
50π
15.证明:(1)平面,平面,
∴AC⊥PD. ……………… 2分
∵,,PD平面PBD,BD平面PBD,
∴AC⊥平面. ……………… 6分
∵平面,
∴AC⊥PB. ……………… 7分
(2)设,连结,
∵,
∴O为中点. ……………… 10分
∵E为中点,
∴EO∥. ……………… 12分
∵平面BDE,PA平面BDE,
∴∥平面 ……………… 14分
证明:(1)∵棱柱ABC-A1B1C1为正三棱柱
∴CC1⊥平面ABC
又∵AD?平面ABC
∴CC1⊥AD
又∵AD⊥C1D,C1D∩CC1=C1,
∴AD⊥面BCC1B1.
(2)连接DE,
∵AB=AC,
∴D为BC的中点,又由E是B1C1的中点,
∴DE∥A1A且DE=A1A
∴四边形A1ADE为平行四边形
∴A1E∥AD
又∵A1E?平面ADC1.AD?平面ADC1.
∴A1E∥平面ADC1.
证明:(1)连接BD交AC于点O,连接FO,
则点O是BD的中点.
∵点F为A1D的中点,∴A1B∥FO.
又A1B?平面AFC,FO?平面AFC,
∴A1B∥平面AFC.
(2)在正方体ABCD﹣A1B1C1D1中,
连接B1D.∵AC⊥BD,AC⊥BB1,
∴AC⊥平面B1BD,AC⊥B1D.
又∵CD⊥平面A1ADD1,AF?平面A1ADD1,
∴CD⊥AF.又∵AF⊥A1D,
∴AF⊥平面A1B1CD.
∵AC⊥B1D,∴B1D⊥平面AFC.
而B1D?平面A1B1CD,
∴平面A1B1CD⊥平面AFC.
3
[1,2]
(苏州市2008-2009高二 理(下)期末)6. 设是球表面上的四个点,两两垂直,且,则求的表面积= 。
(苏州市2008-2009高二 理(下)期末)11. 在正四面体中,分别是棱的中点。
给出下面四个结论:①;②;③;④,其中所有不正确的结论的序号是 。
(苏州市2008-2009高二 理(下)期末)18. 如图,在矩形中,已知,为的中点,现将折起,使点A到点P处,满足PB=PC,设M,H分别为PC,DE的中点。
(1)求证:;
(2)线段上是否存在一点,使?试证明你的结论;
(3)求的面积.
(苏州市2009-2010高二 理(下)期末)8.?棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,
给出下列命题:
????①直线MN∥平面ABC;
????②直线CD⊥平面BMN;
③三棱锥B-AMN的体积是三棱锥B-ACM的体积的一半.
则其中正确命题的序号为????? ?????.
(苏州市2009-2010高二 理(下)期末)17.(本小题满分14分)在斜三棱柱ABC-A1B1C1中,BB1=BA=BC=1,∠B1BC=60°,∠ABC=90°,平面BB1C1C⊥平面ABC,??M、N分别是BC的三等分点.
(1)求证:A1N∥平面AB1M;?
(2)求证:AB⊥B1M;?
(3)求三棱锥A-B1BC的体积V.
(苏州市2010-2011高二 理(下)期末)10.底面边长为2,高为1的正三棱锥的全面积为 .
(苏州市2010-2011高二 理(下)期末)16.(本小题满分14分)如图,已知四边形ABCD是矩形,AD⊥平面ABE,AD=AE,点F在线段DE上,且AF⊥平面BDE.求证:
(1)BE⊥平面ADE;
(2)BE∥平面AFC;
(3)平面AFC⊥平面ADE.
(苏州市2011-2012高二 理(下)期末)10.如图,在四棱锥P ABCD中,已知底面ABCD是矩形,AB 2,AD a,PD⊥平面ABCD,若边AB上存在点M,使得PM⊥CM,则实数a 的取值范围是 .
(苏州市2011-2012高二 理(下)期末)15.(本小题满分14分)在直三棱柱ABC A1B1C1中,AB AC AA1 3a,BC 2a,D是BC的中点,E,F分别是A1A,C1C上一点,且AE CF 2a.
(1)求证:B1F⊥平面ADF;
(2)求三棱锥B1 ADF的体积;
(3)求证:BE∥平面ADF.
(苏州市2012-2013高二 理(下)期末)8.已知正四棱柱ABCD A1B1C1D1的对角线AC1的长为,且AC1与底面所成角的余弦值为,则该正四棱柱的体积为 .
(苏州市2012-2013高二 理(下)期末)10.设m,n是两条不同的直线,,是两个不同的平面,给出下列命题:
① 若∥,,,则∥;② 若∥,m ,n∥,则;
③ 若,m ,n ,则m n; ④ 若,m ,n∥,则∥.
上面命题中,所有真命题的序号为 .
(苏州市2012-2013高二 理(下)期末)15.(本小题满分14分)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD = DE = 2AB = 2,且F是CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求四面体BCEF的体积.
(苏州市2013-2014高二 理(下)期末)11.长方体的三条棱长分别为3,4,5,则此长方体的外接球的表面积为______
(苏州市2013-2014高二 理(下)期末)15.(本小题满分14分)在四棱锥P-ABCD中,PD⊥平面ABCD,AB=BC,BD⊥AC,E为PC的中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PA∥平面BDE.
(苏州市2014-2015高二 理(下)期末)11.如图所示,已知三棱柱的所有棱长均为1,且底面ABC,则三棱锥的体积为 .
(苏州市2014-2015高二 理(下)期末)15.(本小题满分14 分)如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
(1) 求证:;
(2) 如果点E是B1C1 的中点,求证:.
(苏州市2015-2016(2017-2018)高二 理(下)期末)16.正方体ABCD﹣A1B1C1D1中,点F为A1D的中点.
(1)求证:A1B∥平面AFC;
(2)求证:平面A1B1CD⊥平面AFC.
(苏州市2016-2017高二 理(下)期末)1.已知空间向量m=(1,2,-2),则|m|= .
(苏州市2016-2017高二 理(下)期末)13.如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是 .
(苏州市2016-2017高二 理(下)期末)16,如图,在四棱锥P-ABCD中,∠BAD=90°,AD//BC,AD=2BC,AB⊥PA.
(1)求证:平面PAD⊥平面ABCD
(2)若E为PD的中点,求证:CE//平面PAB
答案:
立体几何
3π
证明:(1)取PD的中点F,连接EF,FM
由条件知:FM平行且等于DC的一半,EB平行且等于DC的一半
∴FM∥EB,且FM=EB
则四边形EFMB是平行四边形
则BM∥EF
∵BM?平面PDE,EF?平面PDE
∴BM∥平面PDE;
当N为BC的中点时,BC⊥平面PHN,理由如下:
由题意得,HN为直角梯形BCDE的中位线
∴HN⊥BC
∵PB=PC
∴PN⊥BC
又∵HN∩PN=N
∴BC⊥平面PHN,
由(2)中结论可得,BC⊥PH,
又∵PH⊥DE
故PH⊥底面BCDE
则PH⊥HN,即△PHN为直角三角形
∵AB=2AD=4,E为AB的中点
∴BC=2,HN=3,PH= ,则PN=
∴△PBC的面积S= ?BC?PN=
解(1)连A1B交AB1与O,连OM,
则OM为△A1BN的中位线
∴OM∥A1N
∵A1N?平面AB1M,OM?平面AB1M
∴A1N∥平面AB1M.
(2)∵平面BB1C1C⊥平面ABC,而∠ABC=90°
∴AB⊥BC,AB?平面ABC
∴AB⊥平面BB1C1C
∵B1M?平面BB1C1C
∴AB⊥B1M.
(3)∵AB⊥平面BB1C1C
∴V=×(×1×1×sin600)×1=
3
(1)∵AF⊥平面BDE,BE?平面BDE,AD⊥平面ABE,BE?平面ABE
∴AF⊥BE,AD⊥BE,而AD∩AF=A
∴BE⊥平面ADE;
(2)设AC与BD交于O,连接FO
∵AD=AE,AF⊥DE
∴点F为DE的中点,而O为BD的中点
根据中位线定理可知BE∥FO
而FO?平面AFC,BE?平面AFC
∴BE∥平面AFC;
(3)∵BE⊥平面ADE,BE∥FO
∴FO⊥平面ADE
而FO?平面AFC
∴平面AFC⊥平面ADE.
(0,1]
证明:∵AB AC,D为BC中点,
∴AD⊥BC. …………… 1分
在直三棱柱ABC A1B1C1中,
∵B1B⊥底面ABC,AD底面ABC,
∴AD⊥B1B. …………… 2分
∵BCB1B B,∴AD⊥平面B1BCC1.…………… 3分
∵B1F平面B1BCC1,∴AD⊥B1F. …………… 4分
在矩形B1BCC1中,
∵C1F CD a,B1C1 CF 2a,
∴Rt△DCF ≌ Rt△FC1B1.
∴?CFD ?C1B1F.∴?B1FD 90°.
∴B1F⊥FD. …………………… 5分
∵ADFD D,∴B1F⊥平面AFD. …………… 6分
(2)∵B1F⊥平面AFD,
∴
=. ……………… 10分
(3)连EF,EC,设,连,
,∴四边形AEFC为矩形,为中点.
为中点,. ……………… 12分
平面,平面,
平面. ……………… 14分
2
②
15.证明:(1)取EC中点G,连BG,GF.
∵F是CD的中点,∴FG∥DE,且FG =DE.
又∵AB∥DE,且AB =DE.
∴四边形ABGF为平行四边形.……… 3分
∴AF∥BG.又BG平面BCE,AF平面BCE.
(条件每少一个扣1分,最多扣2分)
∴AF∥平面BCE. …………5分
(2)∵AB 平面ACD,AF平面ACD,
∴AB AF.∵AB∥DE,∴AF DE. ………… 6分
又∵△ACD为正三角形,∴AF CD. ………… 7分
∵BG∥AF,∴BG DE,BG CD. ………… 8分
∵CD ∩ DE = D,∴BG 平面CDE. ………… 9分
(直接用AF∥BG,AF平面CDE,而得到BG 平面CDE.扣1分)
∵BG平面BCE,∴平面BCE⊥平面CDE; ……………11分
(3)四面体BCEF的体积
. ……………14分
50π
15.证明:(1)平面,平面,
∴AC⊥PD. ……………… 2分
∵,,PD平面PBD,BD平面PBD,
∴AC⊥平面. ……………… 6分
∵平面,
∴AC⊥PB. ……………… 7分
(2)设,连结,
∵,
∴O为中点. ……………… 10分
∵E为中点,
∴EO∥. ……………… 12分
∵平面BDE,PA平面BDE,
∴∥平面 ……………… 14分
证明:(1)∵棱柱ABC-A1B1C1为正三棱柱
∴CC1⊥平面ABC
又∵AD?平面ABC
∴CC1⊥AD
又∵AD⊥C1D,C1D∩CC1=C1,
∴AD⊥面BCC1B1.
(2)连接DE,
∵AB=AC,
∴D为BC的中点,又由E是B1C1的中点,
∴DE∥A1A且DE=A1A
∴四边形A1ADE为平行四边形
∴A1E∥AD
又∵A1E?平面ADC1.AD?平面ADC1.
∴A1E∥平面ADC1.
证明:(1)连接BD交AC于点O,连接FO,
则点O是BD的中点.
∵点F为A1D的中点,∴A1B∥FO.
又A1B?平面AFC,FO?平面AFC,
∴A1B∥平面AFC.
(2)在正方体ABCD﹣A1B1C1D1中,
连接B1D.∵AC⊥BD,AC⊥BB1,
∴AC⊥平面B1BD,AC⊥B1D.
又∵CD⊥平面A1ADD1,AF?平面A1ADD1,
∴CD⊥AF.又∵AF⊥A1D,
∴AF⊥平面A1B1CD.
∵AC⊥B1D,∴B1D⊥平面AFC.
而B1D?平面A1B1CD,
∴平面A1B1CD⊥平面AFC.
3
[1,2]
