江苏省苏州市2008-2018学年高二(下)期末数学试卷(理科)分类汇编:选做题
文档属性
| 名称 | 江苏省苏州市2008-2018学年高二(下)期末数学试卷(理科)分类汇编:选做题 | 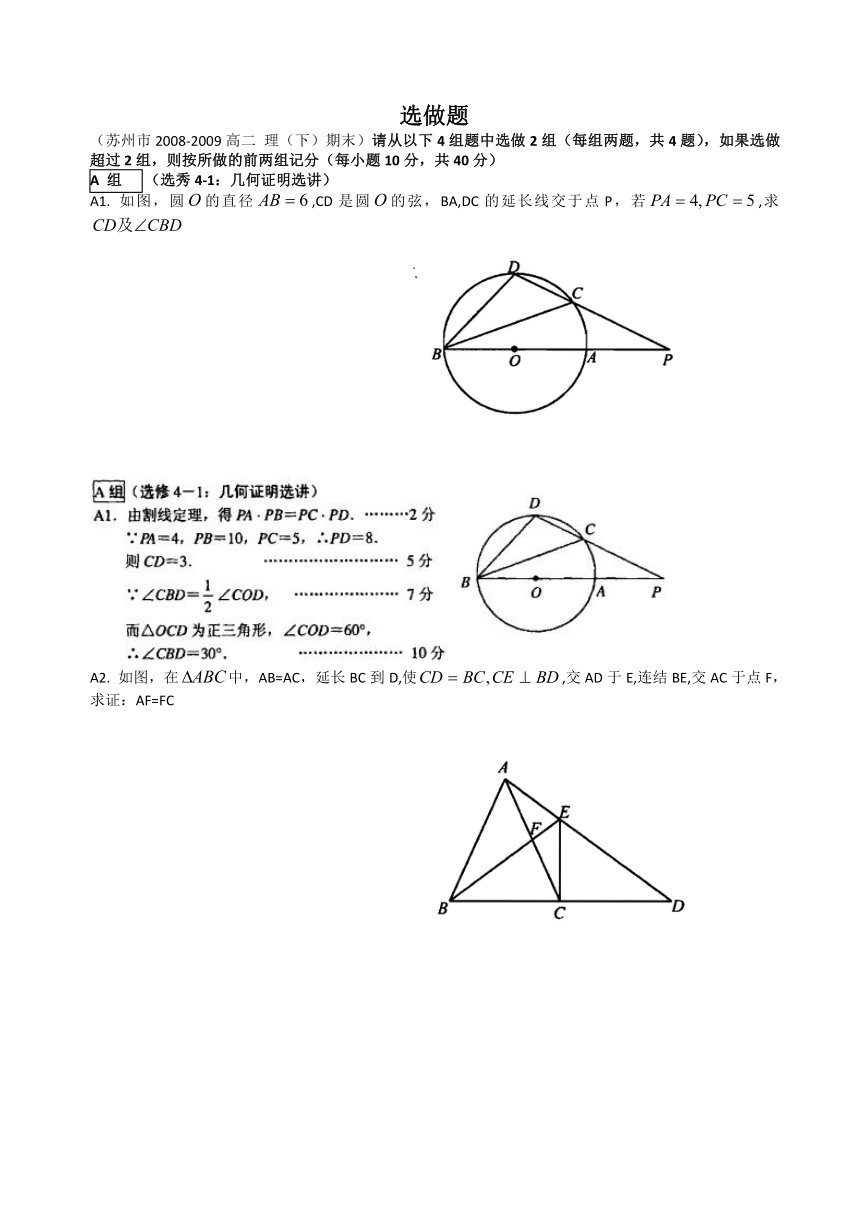 | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 15:55:21 | ||
图片预览




文档简介
选做题
(苏州市2008-2009高二 理(下)期末)请从以下4组题中选做2组(每组两题,共4题),如果选做超过2组,则按所做的前两组记分(每小题10分,共40分)
A 组 (选秀4-1:几何证明选讲)
A1. 如图,圆的直径,CD是圆的弦,BA,DC的延长线交于点P,若,求
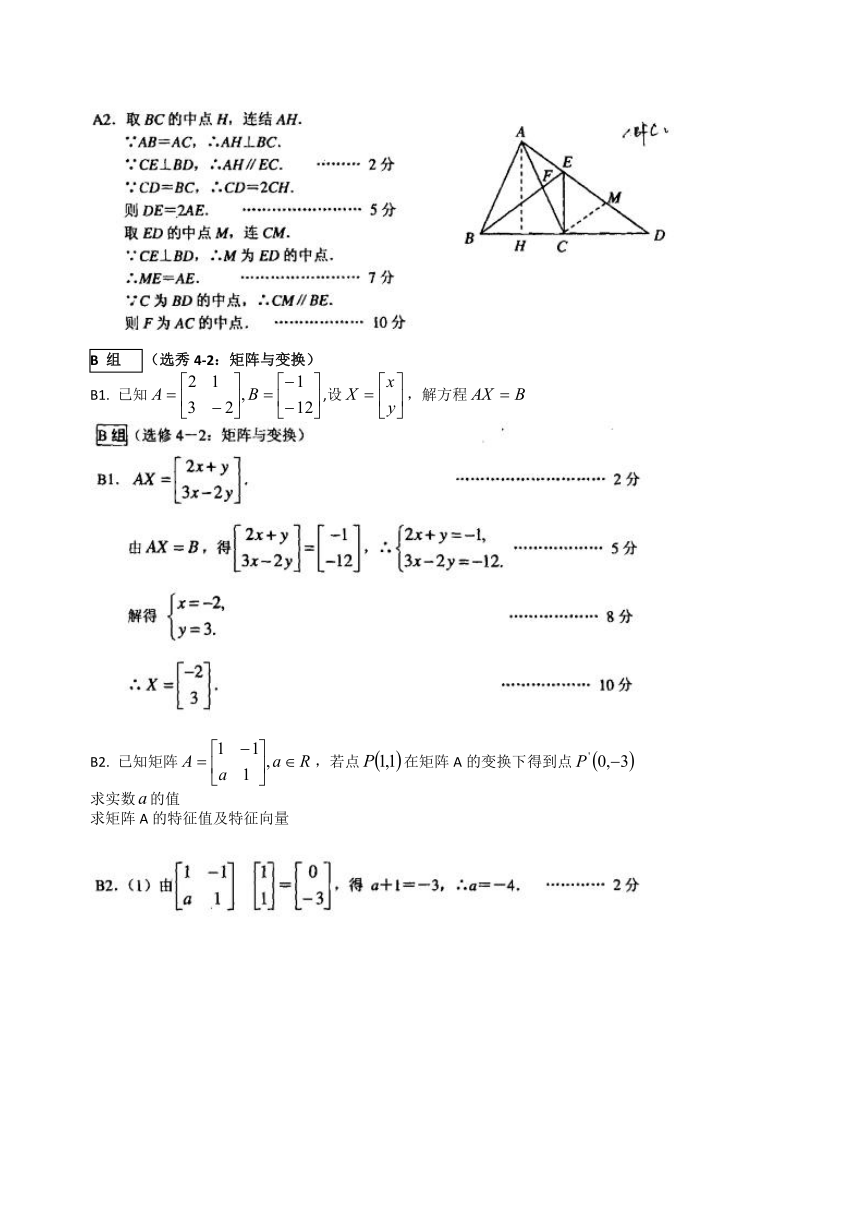
A2. 如图,在中,AB=AC,延长BC到D,使,交AD于E,连结BE,交AC于点F,求证:AF=FC
B 组 (选秀4-2:矩阵与变换)
B1. 已知,设,解方程
B2. 已知矩阵,若点在矩阵A的变换下得到点
求实数的值
求矩阵A的特征值及特征向量
C 组 (选秀4-4:坐标系与参数方程)
C1. 自极点作射线与直线相交于点,在上取一点,使得,求点的轨迹的极坐标方程
C2. 过点作倾斜角为的直线与曲线相交与两点
写出直线的参数方程;
求的最小值。
D 组 (选秀4-5:不等式选讲)
D1. 已知是正数,求证:,并指出等号成立的条件
D2. 设实数满足,试求的最小值
(苏州市2009-2010高二 理(下)期末)
A组(选修4-1:几何证明选讲)
????A1.如图,在RtΔABC中,∠C是直角,AC=3,BC=4,CD⊥AB于点D,∠A的平分线交CD于点M,交BC于点E,求4,求:
(1)CD的长;
????(2)AE的长.
????
解:(1)∵∠C是直角AC=3,BC=4,∴AB=5
由AB×CD=AC×BC得,CD===
(2)由AE是∠A的平分线交CD于点M,交BC于点E,
∴==
故CE=BC=
在Rt△ACE中,由勾股定理,得AE=
A2.如图.过⊙O的弧AB的中点C作弦CD,CE分别与AB相交于点F、G.
????求证:CD·CF=CE·CG
证明:连接AD,DE,EB,
由A,D,E,B四点共圆,得∠ADE+∠B=180°
∵∠ADE=∠ADC+∠CDE
∴∠ADC+∠CDE+∠B=180°①
∵点C是弧AB的中点,
∴∠ADC=∠BEC ②
由①②,得∴∠BEC+∠CDE+∠B=180°,即(∠BEC+∠B)+∠CDE=180°,
∴∠EGA+∠CDE=180°,则四边形DFEG内接于圆
∵直线CFD,CGE是该圆的两条割线
∴CD×CF=CG×CE
B组(选修4-2:矩阵与变换)
????
B1.已知直线L:4x-2y+5=0与x轴,y轴分别交于A,B两点,矩阵M=所对应的变换为TM(a,bR)
(1) 求点A,B在TM作用下所得到的点A’,B’的坐标;
(2) 若变换TM把直线l变换为自身,求M.
解:(1)A(0,),B(-,0),设A′(m,n ),B′(m′,n′)
则==
==
∴A′(,),B′(,).
(2)在直线l上任取一点P(x,y),设点P在TM的变换下变为点P′(x′,y′),
则=,,所以点P′(3x+ay,bx-y),
∵点P′在直线l上,∴4(3x+ay)-2(bx-y)+5=0,即(12-2b)x+(4a+2)y+5=0,
∵方程(12-2b)x+(4a+2)y+5=0即为直线l的方程4x-2y+5=0,
∴,解得?
∴M=.
B2.已知矩阵,向量a=.
(1) 求A的特征值λ1,,λ2和特征向量a1,a2,;
(2)计算A5a .
解:(1)矩阵A的特征多项式为=λ2-5λ+6,
令f(λ)=0,得λ1=2,λ2=3,
当λ1=2时,得,当λ2=3时,得.(7分)
(2)由得,得m=3,n=1.
∴==.
C组(选修4-4:坐标系与参数方程)
C1.已知直线l极坐标方程ρ-ρ+3=0,圆M的极坐标方程ρ=4.以极点为原点,极轴为x轴建立直角坐标系.
(1) 写出直线L与圆M的直角标方程;
(2) 设直线l与圆M交于A、B两点,求AB的长.
(1)∵直线l极坐标方程ρcosθ-ρsinθ+3=0,∴直角坐标方程为 x-y+3=0.
∵圆M的极坐标方程为ρ=4sinθ,故其直角坐标方程为? x2+(y-2)2=4.
(2)圆M的圆心为(0,2),半径等于2,圆心到直线的距离 d==,
∴AB=2=.
C2.已知曲线E的参数方程为(θ为参数,θR)直线l的参数方程为(t为参数,tR)
(1) 求曲线E和直线l的普通方程.
(2) 若点P,Q分别为曲线E,直线l上的动点,求线段PQ长的最小值。
解:(1)曲线E的普通方程为??,直线l的普通方程为 3x+4y-18=0.
(2)设点P(4cosθ,3sinθ),线段PQ≥=≥
,故当PQ与直线l垂直,且 θ=2kπ+,k∈z 时,线段PQ取最小值为?.
D组(选修4-5:不等式选讲)
D1.设ΔABC的三条边为a,b,c,求证:ab+bc+ca≤a2+b2+c2<2(ab+bc+ca)
证明:∵a2+b2≥2ab,b2+c2≥2bc,a2?+c2≥2ac,相加可得 2(a2+b2+c2)≥2ab+2bc+2ac,
∴a2+b2+c2≥ab+bc+ca.
又因为△ABC的三条边为a,b,c,∴a+b>c,b+c>a,a+c>b.
∴a2?-ab-ac=a(a-b-c)<0,a2<ab+ac,同理可得,b2?-<ba+bc,c2?<ca+cb,
相加可得 a2+b2+c2<2(ab+bc+ca).
综上可得 ab+bc+ca≤a2+b2+c2<2(ab+bc+ca)成立.
分析:由基本不等式可证 a2+b2+c2≥ab+bc+ca,根据a2?-ab-ac=a(a-b-c)<0,可得 a2<ab+ac,同理可得b2?-<ba+bc,c2?<ca+cb,相加可得 a2+b2+c2<2(ab+bc+ca),从而证得命题.
点评:本题考查用综合法证明不等式,基本不等式的应用,以及三角形任意两边之和大于第三边,证明a2<ab+ac,是解题的关键.
D2.已知nN*,求证:
(苏州市2010-2011高二 理(下)期末)A组(选修4-1:几何证明选讲)
A1.如图,矩形 ABCD中,AB﹦a,BC﹦b,M为BC的中点,DE⊥AM,垂足
为E,求证: DE=
A2.如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.求证:ED2=EC·EB.
解:如图,因为AE是圆的切线
所以∠ABC=∠CAE.
又因为AD是∠BAC的平分线,
所以∠BAD=∠CAD
从而∠ABC+∠BAD=∠CAE+∠CAD
因为∠ADE=∠ABC+∠BAD,∠DAE=∠CAE+∠CAD
所以∠ADE=∠DAE,故EA=ED
因为EA是圆的切线,所以由切割线定理知,?
EA2= EC·EB
而EA=ED
所以ED2=EC·EB。
B组(选修4-2:矩阵与变换)
B1.设可逆矩阵 A=的逆矩阵A-1=,求实数 a,b的值.
B2.已知点P(1,1)在矩阵A=(a∈R)对应的变换作用下得到点P'(0,-3).
(1)求实数 a的值;
(2)求矩阵 A的特征值及特征向量.
C组(选修4-4:坐标系与参数方程)
C1.在极坐标系中,设圆ρ=3上的点到直线ρ(+)=2,的距离为d,求d的最大值.
C2.矩形ABCD的顶点C的坐标为(4,2),顶点A在椭圆上运动,且AB,AD分别平行于x,y轴,求矩形ABCD面积的取值范围.
D组(选修4-5:不等式选讲)
D1.设x+y+z=1,求M=x2+3y2+z2的最小值.
D2.已知关于x的不等式|x-1|+|x+1|≤++对任意正实数a,b,c恒成立,
求实数x的取值范围.
(苏州市2011-2012高二 理(下)期末)A组(选修4-1:几何证明选讲)
A1.在以AB为直径的半圆上有两点M,N,设弦AN与BM交于点P.
求证:.
A1.证明:作于,
为直径,
. ……………… 3分
四点共圆,四点共圆.
……………… 5分
∴,①
∴.② ……………… 7 分
① ②,得.……… 9分
即. ………………………… 10分
A2.在△ABC中,已知CM是∠ACB的平分线,△AMC的外接圆交BC于点N.若AC =AB,
求证:BN = 2AM.
A2.证明:如图,在△ABC中,
∵CM是∠ACM的平分线,
∴. ………………… 3分
∵, ∴.① ………………… 5分
又∵BA与BC是圆O的两条割线,
∴,即.② ……………… 7分
由①,②可知,. ……………… 9分
∴BN = 2AM. ……………… 10分
B组(选修4-2:矩阵与变换)
B1.已知在二阶矩阵对应变换的作用下,四边形变成四边形,其中,, ,,,.
(1)求出矩阵;(2)确定点及点的坐标.
B1.解:(1)设,
则. …………………… 3分
∴ 解得,.……… 5分
(2)由,得. …………………… 7分
设D(x,y),由,得 ………………… 9分
解得x 1,y 1,∴ . ………………… 10分
B2.给定矩阵=,= 及向量e1 ,e2 .
(1)证明M和N互为逆矩阵;
(2)证明e1和e2都是的特征向量.
B2.解:(1)∵MN = = , …………………… 2分
NM = = ,
∴M和N互为逆矩阵. ……………………… 5分
(2)∵ ==. ……………………… 7分
=. ……………………… 9分
∴e1和e2是M的特征向量. ……………………… 10分
C组(选修4-4:坐标系与参数方程)
C1.在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为,设曲线C与x轴及y轴的交点分别为M,N.
(1)写出曲线C的直角坐标方程,并求M, N的极坐标;
(2)设M,N的中点为P,求直线OP的极坐标方程.
C1.解:(1)由,得,
∴曲线C的直角坐标方程为,即.……………… 3分
当时,,∴M的极坐标为(2,0);
当时,,∴N的极坐标为. ……………… 5分
(2)M的直角坐标为(2,0),N的直角坐标为,
∴P的直角坐标为. ………………… 7分
则P的极坐标为. ………………… 9分
∴直线OP的极坐标方程为. ………………… 10分
C2.过点P(3,0)且倾斜角为30°的直线和曲线相交于A,B两点.求线段AB的长.
C2.解:直线的参数方程为(s为参数),
曲线(t为参数)化为. ………………… 3分
将直线的参数方程代入上式,得. ………………… 5分
设A,B对应的参数分别为,
则. ………………… 7分
∴AB ………………… 9分
. ………………… 10分
D组(选修4-5:不等式选讲)
D1.求函数的最大值.
D1.解: ………………… 3分
由柯西不等式,得
. ………………… 5分
当且仅当时取等号. ………………… 7分
解得. ………………… 9分
∴取得最大值. ………………… 10分
D2.设x,y,z为正数,证明:.
D2.∵,
∴. ………………… 3分
同理,, ………………… 5分
三式相加即可得. ……………… 7分
∵,…………… 9分
∴ . ……………… 10分
(苏州市2012-2013高二 理(下)期末)数学Ⅱ(理科附加题)参考答案
已知三角形ABC中,AB=AC,AD是BC边上的中线,BF||AC,CF交AD于P,交AB于E,求证:BP?=PE×PF
A1 证明:如图,连结,
∵AB = AC,AD是BC边的中线,
∴是此等腰三角形的一条对称轴.
∴. ………… 2分
∵BF∥AC,F = ACP.
∴F = ABP. ………… 5分
又,
∴∽. ………… 8分
所以,即.
∵BP = CP,∴CP2 = PE·PF. ……… 10分
已知,直线AF切三角形ABC外接圆O于点A,交三角形ABC的高CE的延长线于点F,BD垂直AC.求证:(1)(2)
A2 证明:(1)连结.
∵AF为切线,∴FAB = ACB.………… 2分
∵,,
∴.
∴. ………… 5分
(2)∵,,
∴四点共圆.则.
又,∴.
则DE∥AF. ……………8分
∴,即. ……… 10分
已知矩阵,.在平面直角坐标系中,设直线2x﹣y+1=0在矩阵MN对应的变换作用下得到曲线F,求曲线F的方程.
B1 解:由题设得. ………… 2分
设直线上任意一点在矩阵对应的变换作用下变为,
则 . ………… 5分
即,∴ ………… 8分
∵点在直线上,∴,即.
∴曲线的方程为. ………… 10分
矩阵M=(1)a=1,b=2,(2)M 10α
已知点A(1,1)在矩阵M=(a,b,∈R)对应的变换作用下得到点A′(2,2).
(Ⅰ)求矩阵M;
(Ⅱ)M10.
B2 解:(1)由题意得. ………… 2分
即,∴
则. ………… 5分
(2)由(1)得矩阵M ,
矩阵M的特征多项式为,
矩阵M的另一个特征值是1.
代入二元一次方程组,解得,
于是M的属于特征值1的一个特征向量为. ………… 8分
∴α =.
∴M 10α = M 10.………… 10分
已知曲线C的直角坐标方程为x2+y2-2x=0,直线l的直角坐标方程为x-y-4=0极坐标方程是ρ=2,以原点为极点,x轴的正半轴为极轴建立极坐标系?,求过点c且与l垂直的直线的极坐标方程
C1解:圆的直角坐标方程为,即. ………… 2分
圆心,直线的直角坐标方程为x-y-4=0. ………… 5分
所以过点与直线垂直的直线的方程为. ………… 8分
化为极坐标方程得,即.………… 10分
C2 解:(1)直线的普通方程,
椭圆的普通方程为; …………………… 2分
(2)设椭圆上一点的坐标为,
∵m ? 2,∴点到直线的距离
.
∴. …………………… 5分
∵椭圆上有且只有1个点到直线的距离为2,
∴关于的方程在上有且只有一个解.
∴或. …………………… 8分
若,满足,此时,点的坐标是;
若,不合题意.
综上,实数的值为,该点的坐标为.……………10分
D1证明:(1)当时,因为,,
即n = 2时不等式成立; ……… 2分
(2)假设n = k()时不等式成立,即有,
则当时, ……… 5分
. ……… 8分
即当时,不等式也成立.
综合(1)(2)可知,原不等式成立. ……… 10分
D2(1)证明:由柯西不等式得
………… 2分
.
∵,∴. …………………… 5分
(2)解:由(1)得.
当m≥2时,m m 2≤36,∴m≤19;
当时,m 2 m≤36,恒成立;
当m≤0时, m 2 m≤36,∴m≥17. …………………… 8分
综上,实数的取值范围是[17,19]. …………………… 10分
(苏州市2013-2014高二 理(下)期末)
(苏州市2014-2015高二 理(下)期末)数学II(附加题)
请从以下4 组题中选做2 组题作答,如果多做,则按作答的前两组题评分.每小题10 分,共40 分.
A 组[选修4 – 1:几何证明选讲]
A1. 如图,在△ABC 中,CD 是∠ACB的平分线,△ACD 的外接圆交
BC于点E,AB = 2AC.
(1) 求证:BE = 2AD;
(2) 当AC = 1,EC = 2 时,求AD的长.
试题解析:(Ⅰ)连接,因为是圆的内接四边形,所以,又,所以,即有,又,所以,又是的平分线,
所以,从而.
(Ⅱ)由条件的设,根据割线定理得,即,所以即
解得,或(舍去),即
A2. 如图,AB为⊙ O的直径,直线CD 与⊙O相切于点E,AD垂直CD于点D,BC 垂直CD 于点C,EF 垂直AB于点F ,连结AE, BE.
(1) 求证:∠FEB = ∠CEB;
(2) 求证:EF 2 = AD?BC.
(1)由直线CD与⊙O相切,得∠CEB=∠EAB.
由AB为⊙O的直径,得AE⊥EB,从而∠EAB+∠EBF=;
又EF⊥AB,得∠FEB+∠EBF=,从而∠FEB=∠EAB.
故∠FEB=∠CEB.
(2)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,
得Rt△BCE≌Rt△BFE,所以BC=BF.
类似可证:Rt△ADE≌Rt△AFE,得AD=AF.
又在Rt△AEB中,EF⊥AB,故EF2=AF·BF,
所以EF2=AD·BC.
B 组[选修4 – 2:矩阵与变换]
B1. 已知直线在矩阵对应的变换作用下变为直线.
(1) 求实数a, b的值;
(2) 若点在直线???? 上,且满足,求点P的坐标.
(1)设直线l:ax+y=1上任意一点M(x,y)在矩阵A对应的变换作用下的象是M′(x′,y′),
由==,得,又点M′(x′,y′)在l′上,
所以x′+by′=1,即x+(b+2)y=1.依题意解得
(2)A=,得解得y0=0.又点P(x0,y0)在直线l上,所以x0=1,
故点P的坐标为(1,0).
B2. 已知矩阵
(1) 求矩阵M 的特征值及属于每个特征值的一个特征向量;
(2) 求
C 组[选修4 – 4:坐标系与参数方程]
C1. 在平面直角坐标系xoy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知射线:
(t 为参数)相交于A, B 两点.
(1) 写出射线l的参数方程和曲线C的直角坐标方程;
(2) 求线段AB 中点的极坐标.
解:(1)∵射线l:θ=,
∴其直角坐标方程为y=x(x≥0),则射线l的参数方程为,
由曲线C:,消掉t得:y=(x-2)2;
(2)由,得,.
令A(1,1),B(4,4).
则线段AB中点的直角坐标为(),极坐标为().
C2. 在平面直角坐标系xoy 中,以原点O 为极点,???? 轴的非负半轴为极轴建立极坐标系.已知点A的极坐标为(直线l的极坐标方程为且点A在直线l上.
(1) 求a 的值及直线l 的直角坐标方程;
(2) 若圆C的参数方程为为参数),试判断直线l与圆C的位置关系.
(1)由点A(,)在直线ρcos(-)=a上,可得a=,所以直线l的方程可化为,从而直线l的直角坐标方程为.
(2)由已知得圆C的直角坐标方程为(x-1)2+y2=1,所以圆C的圆心为(1,0),半径r=1,因为圆心C到直线l的距离d=<1,所以直线l与圆C相交.
D 组[选修4 – 5:不等式选讲]
D1. 已知函数
(1) 解关于x 的不等式;
(2) 设,若关于x 的不等式的解集不是空集,求实数m的取值范围.
D2. (1) 已知a, b, c 均为正实数,且
(2) 已知a > b > c,且a + b + c = 0,求证:.
(苏州市2015-2016(2017-2018)高二 理(下)期末)请从以下4组中选做2组作答,如果多做,则按作答的前两组题评分.A组[选修4-1:几何证明选讲]
21.如图,在△ABC中,AB=AC,△ABC的外接圆是⊙O,D是劣弧上的一点,弦AD,BC的延长线相交于点E,连结BD并延长到点F,连结CD.
(1)求证:DE平分∠CDF;
(2)求证:AB2=AD?AE.
证明:(1)∵圆O是四边形ABCD的外接圆,
∴∠ABC=∠DEC,
∵AB=AC,∴∠ABC=∠ADB,
∵∠ADB与∠EDF是对顶角,∴∠ADB=∠EDF,
∴∠DEC=∠EDF,
∴DE平分∠CDF.
(2)∵∠ABE=∠ADB,∠BAD=∠BAE,
∴△ABD∽△ABE,
∴,
∴AB2=AD?AE.
22.如图,AD,CF是△ABC的两条高,AD,CF相交于点H,AD的延长线与△ABC的外接圆⊙O相交于点G,AE是⊙O的直径.
(1)求证:AB?AC=AD?AE;
(2)求证:DG=DH.
证明:(1)连接CE,
∵AE是⊙O的直径,∴AC⊥CE,
∵AD是△ABC的两条高,∴AD⊥BC,
∵∠B=∠E,
∴△ADB∽△ACE,
∴,
∴AB?AC=AD?AE;
(2)连接BG,
∵AD、BE、CF分别是△ABC三边的高,H是垂心,
∴∠BEC=90°,∠ADC=90°,
∴∠EBC+∠ECB=∠3+∠ACD,
∴∠EBC=∠3,
∵∠CBG=∠3,
∴∠EBC=∠CBG,
而BD⊥HG,
∴BD平分HG,
即DH=DG.
B组[选修4-2:矩阵与变换]
23.已知矩阵A=,B=
(1)求A的逆矩阵A﹣1;
(2)求矩阵C,使得AC=B.
解:(1)因为|A|=2×3﹣1×4=2,
所以;
(2)由AC=B得(A﹣1A)C=A﹣1B,
故.
24.已知矩阵,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,﹣3),
(1)求实数a的值;
(2)求矩阵A的特征值及特征向量.
解:(1)由=,
得a+1=﹣3
∴a=﹣4
(2)由(1)知,
则矩阵A的特征多项式为
令f(λ)=0,得矩阵A的特征值为﹣1或3
当λ=﹣1时二元一次方程
∴矩阵A的属于特征值﹣1的一个特征向量为
当λ=3时,二元一次方程
∴矩阵A的属于特征值3的一个特征向量为.
C组[选修4-4:坐标系与参数方程]
C组[选修4-4:坐标系与参数方程]
25.在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知曲线C1的极坐标方程为ρ=8,曲线C2的参数方程为,(θ为参数).
(1)将曲线C1的极坐标方程化为直角坐标方程,将曲线C2的参数方程化为普通方程;
(2)若P是曲线C2上的动点,求P到直线l:,(t为参数)的距离的最大值.
【考点】参数方程化成普通方程;简单曲线的极坐标方程.
【分析】(1)将极坐标方程展开,两边同乘ρ,根据极坐标与直角坐标的对应关系得出C1的直角坐标方程,根据同角三角函数的关系消元得出C2的普通方程;
(2)求出直线l的普通方程,根据点到直线的距离公式得出P到直线l的距离d关于θ的函数,利用三角恒等变换得出d的最大值.
【解答】解:(1)∵曲线C1的极坐标方程为ρ=8cos(θ﹣),
∴ρ=8sinθ﹣8cosθ,∴ρ2=8ρsinθ﹣8ρcosθ,
∴曲线C1的极坐标方程为x2+y2﹣8y+8x=0,即(x+4)2+(y﹣4)2=32.
∵曲线C2的参数方程为,(θ为参数)
∴曲线C2的普通方程为.
(2)直线l的普通方程为x﹣2y﹣7=0.
∴P(8cosθ,3sinθ)到直线l的距离d==.
∴当cos(θ+φ)=﹣1时,d取得最大值=.
∴P到直线l的最大距离为.
26.选修4﹣4:坐标系与参数方程
曲线C1的参数方程为(α为参数),在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为.
(1)求曲线C1的极坐标方程和曲线C2的直角坐标方程;
(2)若射线l:y=kx(x≥0)与曲线C1,C2的交点分别为A,B(A,B异于原点),当斜率k∈(1,]时,求|OA|?|OB|的取值范围.
【考点】参数方程化成普通方程.
【分析】(1)先将C1的参数方程化为普通方程,再华为极坐标方程,将C2的极坐标方程两边同乘ρ,根据极坐标与直角坐标的对应关系得出C2的直角坐标方程;
(2)求出l的参数方程,分别代入C1,C2的普通方程,根据参数的几何意义得出|OA|,|OB|,得到|OA|?|OB|关于k的函数,根据k的范围得出答案.
【解答】解:(1)曲线C1的直角坐标方程为(x﹣1)2+y2=1,即x2+y2﹣2x=0,
∴曲线C1的极坐标方程为ρ2﹣2ρcosθ=0,即ρ=2cosθ.
∵曲线C2的极坐标方程为ρcos2θ=sinθ,即ρ2cos2θ=ρsinθ,
∴曲线C2的直角坐标方程为x2=y.
(2)设射线l的倾斜角为α,
则射线l的参数方程为(t为参数,).
把射线l的参数方程代入曲线C1的普通方程得:t2﹣2tcosα=0,
解得t1=0,t2=2cosα.
∴|OA|=|t2|=2cosα.
把射线l的参数方程代入曲线C2的普通方程得:cos2αt2=tsinα,
解得t1=0,t2=.
∴|OB|=|t2|=.
∴|OA|?|OB|=2cosα?=2tanα=2k.
∵k∈(1,],∴2k∈(2,2].
∴|OA|?|OB|的取值范围是(2,2].
D组[选修4-5:不等式选讲]
27.已知关于x的不等式|ax﹣1|+a|x﹣1|≥1(a>0).
(1)当a=1时,求此不等式的解集;
(2)若此不等式的解集是R,求正实数a的取值范围.
【考点】绝对值三角不等式;绝对值不等式的解法.
【分析】(1)当a=1时,可得2|x﹣1|≥1,即|x﹣1|≥,由此求得不等式的解集.
(2)不等式|ax﹣1|+|ax﹣a|≥1解集为R,等价于|a﹣1|≥1,由此求得实数a的取值范围.
【解答】解:(1)当a=1时,可得2|x﹣1|≥1,即|x﹣1|≥,解得x﹣1≥或x﹣1≤﹣,∴x≥或x≤﹣
∴不等式的解集为(﹣∞,﹣]∪[,+∞). …
(2)∵|ax﹣1|+|ax﹣a|≥|a﹣1|,不等式|ax﹣1|+|ax﹣a|≥1解集为R,等价于|a﹣1|≥1.
解得a≥2,或a≤0. 又∵a>0,∴a≥2.
∴实数a的取值范围为[2,+∞). …
28.已知a,b,c均为正实数,求证:
(1)+≥;
(2)++≥++.
【考点】不等式的证明.
【分析】(1)运用两个正数的均值不等式,可得a+b≥2, +≥2,相乘即可得证;
(2)由(1)可得+≥;同理可得+≥; +≥.三式相加,整理即可得证.
【解答】证明:(1)a,b均为正实数,
可得a+b≥2,
+≥2,
相乘可得(a+b)(+)≥2?2=4,
当且仅当a=b,取得等号.
则+≥;
(2)由(1)可得+≥;
同理,由b,c为正实数,可得+≥;
由c,a为正实数,可得+≥.
相加可得,2(++)≥++,
即有++≥++.
(苏州市2016-2017高二 理(下)期末)
A组(选修4-2矩阵与变换)
A1、已知矩阵A=,B=
(1)求矩阵A的逆矩阵
(2)若矩阵X满足AX=B,试求曲线y=x2在矩阵X对应的变换作用下得到的曲线方程
A2、已知二阶矩阵M=,α=
(1)求矩阵M的特征值域特征向量
(2)求M5α
B组(选修4-4:坐标系与参数方程)
B1、在平面直角坐标系xOy中,曲线C的参数方程为,(θ为参数)
(1)写出曲线C的直角坐标系方程
(2)若直线l经过点A(0,),倾斜角为45°,且与曲线C交于两M,N点,求MN的长.
B2、在平面直角坐标系xOy中,直线AB的参数方程为,(t为参数),以原点为极点,x正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=
2sin(θ+)(ρ≥0)
(1)求曲线C的参数方程
(2)设点M为曲线C上的动点,求点M与直线AB距离d的最小值.
11
(苏州市2008-2009高二 理(下)期末)请从以下4组题中选做2组(每组两题,共4题),如果选做超过2组,则按所做的前两组记分(每小题10分,共40分)
A 组 (选秀4-1:几何证明选讲)
A1. 如图,圆的直径,CD是圆的弦,BA,DC的延长线交于点P,若,求
A2. 如图,在中,AB=AC,延长BC到D,使,交AD于E,连结BE,交AC于点F,求证:AF=FC
B 组 (选秀4-2:矩阵与变换)
B1. 已知,设,解方程
B2. 已知矩阵,若点在矩阵A的变换下得到点
求实数的值
求矩阵A的特征值及特征向量
C 组 (选秀4-4:坐标系与参数方程)
C1. 自极点作射线与直线相交于点,在上取一点,使得,求点的轨迹的极坐标方程
C2. 过点作倾斜角为的直线与曲线相交与两点
写出直线的参数方程;
求的最小值。
D 组 (选秀4-5:不等式选讲)
D1. 已知是正数,求证:,并指出等号成立的条件
D2. 设实数满足,试求的最小值
(苏州市2009-2010高二 理(下)期末)
A组(选修4-1:几何证明选讲)
????A1.如图,在RtΔABC中,∠C是直角,AC=3,BC=4,CD⊥AB于点D,∠A的平分线交CD于点M,交BC于点E,求4,求:
(1)CD的长;
????(2)AE的长.
????
解:(1)∵∠C是直角AC=3,BC=4,∴AB=5
由AB×CD=AC×BC得,CD===
(2)由AE是∠A的平分线交CD于点M,交BC于点E,
∴==
故CE=BC=
在Rt△ACE中,由勾股定理,得AE=
A2.如图.过⊙O的弧AB的中点C作弦CD,CE分别与AB相交于点F、G.
????求证:CD·CF=CE·CG
证明:连接AD,DE,EB,
由A,D,E,B四点共圆,得∠ADE+∠B=180°
∵∠ADE=∠ADC+∠CDE
∴∠ADC+∠CDE+∠B=180°①
∵点C是弧AB的中点,
∴∠ADC=∠BEC ②
由①②,得∴∠BEC+∠CDE+∠B=180°,即(∠BEC+∠B)+∠CDE=180°,
∴∠EGA+∠CDE=180°,则四边形DFEG内接于圆
∵直线CFD,CGE是该圆的两条割线
∴CD×CF=CG×CE
B组(选修4-2:矩阵与变换)
????
B1.已知直线L:4x-2y+5=0与x轴,y轴分别交于A,B两点,矩阵M=所对应的变换为TM(a,bR)
(1) 求点A,B在TM作用下所得到的点A’,B’的坐标;
(2) 若变换TM把直线l变换为自身,求M.
解:(1)A(0,),B(-,0),设A′(m,n ),B′(m′,n′)
则==
==
∴A′(,),B′(,).
(2)在直线l上任取一点P(x,y),设点P在TM的变换下变为点P′(x′,y′),
则=,,所以点P′(3x+ay,bx-y),
∵点P′在直线l上,∴4(3x+ay)-2(bx-y)+5=0,即(12-2b)x+(4a+2)y+5=0,
∵方程(12-2b)x+(4a+2)y+5=0即为直线l的方程4x-2y+5=0,
∴,解得?
∴M=.
B2.已知矩阵,向量a=.
(1) 求A的特征值λ1,,λ2和特征向量a1,a2,;
(2)计算A5a .
解:(1)矩阵A的特征多项式为=λ2-5λ+6,
令f(λ)=0,得λ1=2,λ2=3,
当λ1=2时,得,当λ2=3时,得.(7分)
(2)由得,得m=3,n=1.
∴==.
C组(选修4-4:坐标系与参数方程)
C1.已知直线l极坐标方程ρ-ρ+3=0,圆M的极坐标方程ρ=4.以极点为原点,极轴为x轴建立直角坐标系.
(1) 写出直线L与圆M的直角标方程;
(2) 设直线l与圆M交于A、B两点,求AB的长.
(1)∵直线l极坐标方程ρcosθ-ρsinθ+3=0,∴直角坐标方程为 x-y+3=0.
∵圆M的极坐标方程为ρ=4sinθ,故其直角坐标方程为? x2+(y-2)2=4.
(2)圆M的圆心为(0,2),半径等于2,圆心到直线的距离 d==,
∴AB=2=.
C2.已知曲线E的参数方程为(θ为参数,θR)直线l的参数方程为(t为参数,tR)
(1) 求曲线E和直线l的普通方程.
(2) 若点P,Q分别为曲线E,直线l上的动点,求线段PQ长的最小值。
解:(1)曲线E的普通方程为??,直线l的普通方程为 3x+4y-18=0.
(2)设点P(4cosθ,3sinθ),线段PQ≥=≥
,故当PQ与直线l垂直,且 θ=2kπ+,k∈z 时,线段PQ取最小值为?.
D组(选修4-5:不等式选讲)
D1.设ΔABC的三条边为a,b,c,求证:ab+bc+ca≤a2+b2+c2<2(ab+bc+ca)
证明:∵a2+b2≥2ab,b2+c2≥2bc,a2?+c2≥2ac,相加可得 2(a2+b2+c2)≥2ab+2bc+2ac,
∴a2+b2+c2≥ab+bc+ca.
又因为△ABC的三条边为a,b,c,∴a+b>c,b+c>a,a+c>b.
∴a2?-ab-ac=a(a-b-c)<0,a2<ab+ac,同理可得,b2?-<ba+bc,c2?<ca+cb,
相加可得 a2+b2+c2<2(ab+bc+ca).
综上可得 ab+bc+ca≤a2+b2+c2<2(ab+bc+ca)成立.
分析:由基本不等式可证 a2+b2+c2≥ab+bc+ca,根据a2?-ab-ac=a(a-b-c)<0,可得 a2<ab+ac,同理可得b2?-<ba+bc,c2?<ca+cb,相加可得 a2+b2+c2<2(ab+bc+ca),从而证得命题.
点评:本题考查用综合法证明不等式,基本不等式的应用,以及三角形任意两边之和大于第三边,证明a2<ab+ac,是解题的关键.
D2.已知nN*,求证:
(苏州市2010-2011高二 理(下)期末)A组(选修4-1:几何证明选讲)
A1.如图,矩形 ABCD中,AB﹦a,BC﹦b,M为BC的中点,DE⊥AM,垂足
为E,求证: DE=
A2.如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.求证:ED2=EC·EB.
解:如图,因为AE是圆的切线
所以∠ABC=∠CAE.
又因为AD是∠BAC的平分线,
所以∠BAD=∠CAD
从而∠ABC+∠BAD=∠CAE+∠CAD
因为∠ADE=∠ABC+∠BAD,∠DAE=∠CAE+∠CAD
所以∠ADE=∠DAE,故EA=ED
因为EA是圆的切线,所以由切割线定理知,?
EA2= EC·EB
而EA=ED
所以ED2=EC·EB。
B组(选修4-2:矩阵与变换)
B1.设可逆矩阵 A=的逆矩阵A-1=,求实数 a,b的值.
B2.已知点P(1,1)在矩阵A=(a∈R)对应的变换作用下得到点P'(0,-3).
(1)求实数 a的值;
(2)求矩阵 A的特征值及特征向量.
C组(选修4-4:坐标系与参数方程)
C1.在极坐标系中,设圆ρ=3上的点到直线ρ(+)=2,的距离为d,求d的最大值.
C2.矩形ABCD的顶点C的坐标为(4,2),顶点A在椭圆上运动,且AB,AD分别平行于x,y轴,求矩形ABCD面积的取值范围.
D组(选修4-5:不等式选讲)
D1.设x+y+z=1,求M=x2+3y2+z2的最小值.
D2.已知关于x的不等式|x-1|+|x+1|≤++对任意正实数a,b,c恒成立,
求实数x的取值范围.
(苏州市2011-2012高二 理(下)期末)A组(选修4-1:几何证明选讲)
A1.在以AB为直径的半圆上有两点M,N,设弦AN与BM交于点P.
求证:.
A1.证明:作于,
为直径,
. ……………… 3分
四点共圆,四点共圆.
……………… 5分
∴,①
∴.② ……………… 7 分
① ②,得.……… 9分
即. ………………………… 10分
A2.在△ABC中,已知CM是∠ACB的平分线,△AMC的外接圆交BC于点N.若AC =AB,
求证:BN = 2AM.
A2.证明:如图,在△ABC中,
∵CM是∠ACM的平分线,
∴. ………………… 3分
∵, ∴.① ………………… 5分
又∵BA与BC是圆O的两条割线,
∴,即.② ……………… 7分
由①,②可知,. ……………… 9分
∴BN = 2AM. ……………… 10分
B组(选修4-2:矩阵与变换)
B1.已知在二阶矩阵对应变换的作用下,四边形变成四边形,其中,, ,,,.
(1)求出矩阵;(2)确定点及点的坐标.
B1.解:(1)设,
则. …………………… 3分
∴ 解得,.……… 5分
(2)由,得. …………………… 7分
设D(x,y),由,得 ………………… 9分
解得x 1,y 1,∴ . ………………… 10分
B2.给定矩阵=,= 及向量e1 ,e2 .
(1)证明M和N互为逆矩阵;
(2)证明e1和e2都是的特征向量.
B2.解:(1)∵MN = = , …………………… 2分
NM = = ,
∴M和N互为逆矩阵. ……………………… 5分
(2)∵ ==. ……………………… 7分
=. ……………………… 9分
∴e1和e2是M的特征向量. ……………………… 10分
C组(选修4-4:坐标系与参数方程)
C1.在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为,设曲线C与x轴及y轴的交点分别为M,N.
(1)写出曲线C的直角坐标方程,并求M, N的极坐标;
(2)设M,N的中点为P,求直线OP的极坐标方程.
C1.解:(1)由,得,
∴曲线C的直角坐标方程为,即.……………… 3分
当时,,∴M的极坐标为(2,0);
当时,,∴N的极坐标为. ……………… 5分
(2)M的直角坐标为(2,0),N的直角坐标为,
∴P的直角坐标为. ………………… 7分
则P的极坐标为. ………………… 9分
∴直线OP的极坐标方程为. ………………… 10分
C2.过点P(3,0)且倾斜角为30°的直线和曲线相交于A,B两点.求线段AB的长.
C2.解:直线的参数方程为(s为参数),
曲线(t为参数)化为. ………………… 3分
将直线的参数方程代入上式,得. ………………… 5分
设A,B对应的参数分别为,
则. ………………… 7分
∴AB ………………… 9分
. ………………… 10分
D组(选修4-5:不等式选讲)
D1.求函数的最大值.
D1.解: ………………… 3分
由柯西不等式,得
. ………………… 5分
当且仅当时取等号. ………………… 7分
解得. ………………… 9分
∴取得最大值. ………………… 10分
D2.设x,y,z为正数,证明:.
D2.∵,
∴. ………………… 3分
同理,, ………………… 5分
三式相加即可得. ……………… 7分
∵,…………… 9分
∴ . ……………… 10分
(苏州市2012-2013高二 理(下)期末)数学Ⅱ(理科附加题)参考答案
已知三角形ABC中,AB=AC,AD是BC边上的中线,BF||AC,CF交AD于P,交AB于E,求证:BP?=PE×PF
A1 证明:如图,连结,
∵AB = AC,AD是BC边的中线,
∴是此等腰三角形的一条对称轴.
∴. ………… 2分
∵BF∥AC,F = ACP.
∴F = ABP. ………… 5分
又,
∴∽. ………… 8分
所以,即.
∵BP = CP,∴CP2 = PE·PF. ……… 10分
已知,直线AF切三角形ABC外接圆O于点A,交三角形ABC的高CE的延长线于点F,BD垂直AC.求证:(1)(2)
A2 证明:(1)连结.
∵AF为切线,∴FAB = ACB.………… 2分
∵,,
∴.
∴. ………… 5分
(2)∵,,
∴四点共圆.则.
又,∴.
则DE∥AF. ……………8分
∴,即. ……… 10分
已知矩阵,.在平面直角坐标系中,设直线2x﹣y+1=0在矩阵MN对应的变换作用下得到曲线F,求曲线F的方程.
B1 解:由题设得. ………… 2分
设直线上任意一点在矩阵对应的变换作用下变为,
则 . ………… 5分
即,∴ ………… 8分
∵点在直线上,∴,即.
∴曲线的方程为. ………… 10分
矩阵M=(1)a=1,b=2,(2)M 10α
已知点A(1,1)在矩阵M=(a,b,∈R)对应的变换作用下得到点A′(2,2).
(Ⅰ)求矩阵M;
(Ⅱ)M10.
B2 解:(1)由题意得. ………… 2分
即,∴
则. ………… 5分
(2)由(1)得矩阵M ,
矩阵M的特征多项式为,
矩阵M的另一个特征值是1.
代入二元一次方程组,解得,
于是M的属于特征值1的一个特征向量为. ………… 8分
∴α =.
∴M 10α = M 10.………… 10分
已知曲线C的直角坐标方程为x2+y2-2x=0,直线l的直角坐标方程为x-y-4=0极坐标方程是ρ=2,以原点为极点,x轴的正半轴为极轴建立极坐标系?,求过点c且与l垂直的直线的极坐标方程
C1解:圆的直角坐标方程为,即. ………… 2分
圆心,直线的直角坐标方程为x-y-4=0. ………… 5分
所以过点与直线垂直的直线的方程为. ………… 8分
化为极坐标方程得,即.………… 10分
C2 解:(1)直线的普通方程,
椭圆的普通方程为; …………………… 2分
(2)设椭圆上一点的坐标为,
∵m ? 2,∴点到直线的距离
.
∴. …………………… 5分
∵椭圆上有且只有1个点到直线的距离为2,
∴关于的方程在上有且只有一个解.
∴或. …………………… 8分
若,满足,此时,点的坐标是;
若,不合题意.
综上,实数的值为,该点的坐标为.……………10分
D1证明:(1)当时,因为,,
即n = 2时不等式成立; ……… 2分
(2)假设n = k()时不等式成立,即有,
则当时, ……… 5分
. ……… 8分
即当时,不等式也成立.
综合(1)(2)可知,原不等式成立. ……… 10分
D2(1)证明:由柯西不等式得
………… 2分
.
∵,∴. …………………… 5分
(2)解:由(1)得.
当m≥2时,m m 2≤36,∴m≤19;
当时,m 2 m≤36,恒成立;
当m≤0时, m 2 m≤36,∴m≥17. …………………… 8分
综上,实数的取值范围是[17,19]. …………………… 10分
(苏州市2013-2014高二 理(下)期末)
(苏州市2014-2015高二 理(下)期末)数学II(附加题)
请从以下4 组题中选做2 组题作答,如果多做,则按作答的前两组题评分.每小题10 分,共40 分.
A 组[选修4 – 1:几何证明选讲]
A1. 如图,在△ABC 中,CD 是∠ACB的平分线,△ACD 的外接圆交
BC于点E,AB = 2AC.
(1) 求证:BE = 2AD;
(2) 当AC = 1,EC = 2 时,求AD的长.
试题解析:(Ⅰ)连接,因为是圆的内接四边形,所以,又,所以,即有,又,所以,又是的平分线,
所以,从而.
(Ⅱ)由条件的设,根据割线定理得,即,所以即
解得,或(舍去),即
A2. 如图,AB为⊙ O的直径,直线CD 与⊙O相切于点E,AD垂直CD于点D,BC 垂直CD 于点C,EF 垂直AB于点F ,连结AE, BE.
(1) 求证:∠FEB = ∠CEB;
(2) 求证:EF 2 = AD?BC.
(1)由直线CD与⊙O相切,得∠CEB=∠EAB.
由AB为⊙O的直径,得AE⊥EB,从而∠EAB+∠EBF=;
又EF⊥AB,得∠FEB+∠EBF=,从而∠FEB=∠EAB.
故∠FEB=∠CEB.
(2)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,
得Rt△BCE≌Rt△BFE,所以BC=BF.
类似可证:Rt△ADE≌Rt△AFE,得AD=AF.
又在Rt△AEB中,EF⊥AB,故EF2=AF·BF,
所以EF2=AD·BC.
B 组[选修4 – 2:矩阵与变换]
B1. 已知直线在矩阵对应的变换作用下变为直线.
(1) 求实数a, b的值;
(2) 若点在直线???? 上,且满足,求点P的坐标.
(1)设直线l:ax+y=1上任意一点M(x,y)在矩阵A对应的变换作用下的象是M′(x′,y′),
由==,得,又点M′(x′,y′)在l′上,
所以x′+by′=1,即x+(b+2)y=1.依题意解得
(2)A=,得解得y0=0.又点P(x0,y0)在直线l上,所以x0=1,
故点P的坐标为(1,0).
B2. 已知矩阵
(1) 求矩阵M 的特征值及属于每个特征值的一个特征向量;
(2) 求
C 组[选修4 – 4:坐标系与参数方程]
C1. 在平面直角坐标系xoy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知射线:
(t 为参数)相交于A, B 两点.
(1) 写出射线l的参数方程和曲线C的直角坐标方程;
(2) 求线段AB 中点的极坐标.
解:(1)∵射线l:θ=,
∴其直角坐标方程为y=x(x≥0),则射线l的参数方程为,
由曲线C:,消掉t得:y=(x-2)2;
(2)由,得,.
令A(1,1),B(4,4).
则线段AB中点的直角坐标为(),极坐标为().
C2. 在平面直角坐标系xoy 中,以原点O 为极点,???? 轴的非负半轴为极轴建立极坐标系.已知点A的极坐标为(直线l的极坐标方程为且点A在直线l上.
(1) 求a 的值及直线l 的直角坐标方程;
(2) 若圆C的参数方程为为参数),试判断直线l与圆C的位置关系.
(1)由点A(,)在直线ρcos(-)=a上,可得a=,所以直线l的方程可化为,从而直线l的直角坐标方程为.
(2)由已知得圆C的直角坐标方程为(x-1)2+y2=1,所以圆C的圆心为(1,0),半径r=1,因为圆心C到直线l的距离d=<1,所以直线l与圆C相交.
D 组[选修4 – 5:不等式选讲]
D1. 已知函数
(1) 解关于x 的不等式;
(2) 设,若关于x 的不等式的解集不是空集,求实数m的取值范围.
D2. (1) 已知a, b, c 均为正实数,且
(2) 已知a > b > c,且a + b + c = 0,求证:.
(苏州市2015-2016(2017-2018)高二 理(下)期末)请从以下4组中选做2组作答,如果多做,则按作答的前两组题评分.A组[选修4-1:几何证明选讲]
21.如图,在△ABC中,AB=AC,△ABC的外接圆是⊙O,D是劣弧上的一点,弦AD,BC的延长线相交于点E,连结BD并延长到点F,连结CD.
(1)求证:DE平分∠CDF;
(2)求证:AB2=AD?AE.
证明:(1)∵圆O是四边形ABCD的外接圆,
∴∠ABC=∠DEC,
∵AB=AC,∴∠ABC=∠ADB,
∵∠ADB与∠EDF是对顶角,∴∠ADB=∠EDF,
∴∠DEC=∠EDF,
∴DE平分∠CDF.
(2)∵∠ABE=∠ADB,∠BAD=∠BAE,
∴△ABD∽△ABE,
∴,
∴AB2=AD?AE.
22.如图,AD,CF是△ABC的两条高,AD,CF相交于点H,AD的延长线与△ABC的外接圆⊙O相交于点G,AE是⊙O的直径.
(1)求证:AB?AC=AD?AE;
(2)求证:DG=DH.
证明:(1)连接CE,
∵AE是⊙O的直径,∴AC⊥CE,
∵AD是△ABC的两条高,∴AD⊥BC,
∵∠B=∠E,
∴△ADB∽△ACE,
∴,
∴AB?AC=AD?AE;
(2)连接BG,
∵AD、BE、CF分别是△ABC三边的高,H是垂心,
∴∠BEC=90°,∠ADC=90°,
∴∠EBC+∠ECB=∠3+∠ACD,
∴∠EBC=∠3,
∵∠CBG=∠3,
∴∠EBC=∠CBG,
而BD⊥HG,
∴BD平分HG,
即DH=DG.
B组[选修4-2:矩阵与变换]
23.已知矩阵A=,B=
(1)求A的逆矩阵A﹣1;
(2)求矩阵C,使得AC=B.
解:(1)因为|A|=2×3﹣1×4=2,
所以;
(2)由AC=B得(A﹣1A)C=A﹣1B,
故.
24.已知矩阵,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,﹣3),
(1)求实数a的值;
(2)求矩阵A的特征值及特征向量.
解:(1)由=,
得a+1=﹣3
∴a=﹣4
(2)由(1)知,
则矩阵A的特征多项式为
令f(λ)=0,得矩阵A的特征值为﹣1或3
当λ=﹣1时二元一次方程
∴矩阵A的属于特征值﹣1的一个特征向量为
当λ=3时,二元一次方程
∴矩阵A的属于特征值3的一个特征向量为.
C组[选修4-4:坐标系与参数方程]
C组[选修4-4:坐标系与参数方程]
25.在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知曲线C1的极坐标方程为ρ=8,曲线C2的参数方程为,(θ为参数).
(1)将曲线C1的极坐标方程化为直角坐标方程,将曲线C2的参数方程化为普通方程;
(2)若P是曲线C2上的动点,求P到直线l:,(t为参数)的距离的最大值.
【考点】参数方程化成普通方程;简单曲线的极坐标方程.
【分析】(1)将极坐标方程展开,两边同乘ρ,根据极坐标与直角坐标的对应关系得出C1的直角坐标方程,根据同角三角函数的关系消元得出C2的普通方程;
(2)求出直线l的普通方程,根据点到直线的距离公式得出P到直线l的距离d关于θ的函数,利用三角恒等变换得出d的最大值.
【解答】解:(1)∵曲线C1的极坐标方程为ρ=8cos(θ﹣),
∴ρ=8sinθ﹣8cosθ,∴ρ2=8ρsinθ﹣8ρcosθ,
∴曲线C1的极坐标方程为x2+y2﹣8y+8x=0,即(x+4)2+(y﹣4)2=32.
∵曲线C2的参数方程为,(θ为参数)
∴曲线C2的普通方程为.
(2)直线l的普通方程为x﹣2y﹣7=0.
∴P(8cosθ,3sinθ)到直线l的距离d==.
∴当cos(θ+φ)=﹣1时,d取得最大值=.
∴P到直线l的最大距离为.
26.选修4﹣4:坐标系与参数方程
曲线C1的参数方程为(α为参数),在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为.
(1)求曲线C1的极坐标方程和曲线C2的直角坐标方程;
(2)若射线l:y=kx(x≥0)与曲线C1,C2的交点分别为A,B(A,B异于原点),当斜率k∈(1,]时,求|OA|?|OB|的取值范围.
【考点】参数方程化成普通方程.
【分析】(1)先将C1的参数方程化为普通方程,再华为极坐标方程,将C2的极坐标方程两边同乘ρ,根据极坐标与直角坐标的对应关系得出C2的直角坐标方程;
(2)求出l的参数方程,分别代入C1,C2的普通方程,根据参数的几何意义得出|OA|,|OB|,得到|OA|?|OB|关于k的函数,根据k的范围得出答案.
【解答】解:(1)曲线C1的直角坐标方程为(x﹣1)2+y2=1,即x2+y2﹣2x=0,
∴曲线C1的极坐标方程为ρ2﹣2ρcosθ=0,即ρ=2cosθ.
∵曲线C2的极坐标方程为ρcos2θ=sinθ,即ρ2cos2θ=ρsinθ,
∴曲线C2的直角坐标方程为x2=y.
(2)设射线l的倾斜角为α,
则射线l的参数方程为(t为参数,).
把射线l的参数方程代入曲线C1的普通方程得:t2﹣2tcosα=0,
解得t1=0,t2=2cosα.
∴|OA|=|t2|=2cosα.
把射线l的参数方程代入曲线C2的普通方程得:cos2αt2=tsinα,
解得t1=0,t2=.
∴|OB|=|t2|=.
∴|OA|?|OB|=2cosα?=2tanα=2k.
∵k∈(1,],∴2k∈(2,2].
∴|OA|?|OB|的取值范围是(2,2].
D组[选修4-5:不等式选讲]
27.已知关于x的不等式|ax﹣1|+a|x﹣1|≥1(a>0).
(1)当a=1时,求此不等式的解集;
(2)若此不等式的解集是R,求正实数a的取值范围.
【考点】绝对值三角不等式;绝对值不等式的解法.
【分析】(1)当a=1时,可得2|x﹣1|≥1,即|x﹣1|≥,由此求得不等式的解集.
(2)不等式|ax﹣1|+|ax﹣a|≥1解集为R,等价于|a﹣1|≥1,由此求得实数a的取值范围.
【解答】解:(1)当a=1时,可得2|x﹣1|≥1,即|x﹣1|≥,解得x﹣1≥或x﹣1≤﹣,∴x≥或x≤﹣
∴不等式的解集为(﹣∞,﹣]∪[,+∞). …
(2)∵|ax﹣1|+|ax﹣a|≥|a﹣1|,不等式|ax﹣1|+|ax﹣a|≥1解集为R,等价于|a﹣1|≥1.
解得a≥2,或a≤0. 又∵a>0,∴a≥2.
∴实数a的取值范围为[2,+∞). …
28.已知a,b,c均为正实数,求证:
(1)+≥;
(2)++≥++.
【考点】不等式的证明.
【分析】(1)运用两个正数的均值不等式,可得a+b≥2, +≥2,相乘即可得证;
(2)由(1)可得+≥;同理可得+≥; +≥.三式相加,整理即可得证.
【解答】证明:(1)a,b均为正实数,
可得a+b≥2,
+≥2,
相乘可得(a+b)(+)≥2?2=4,
当且仅当a=b,取得等号.
则+≥;
(2)由(1)可得+≥;
同理,由b,c为正实数,可得+≥;
由c,a为正实数,可得+≥.
相加可得,2(++)≥++,
即有++≥++.
(苏州市2016-2017高二 理(下)期末)
A组(选修4-2矩阵与变换)
A1、已知矩阵A=,B=
(1)求矩阵A的逆矩阵
(2)若矩阵X满足AX=B,试求曲线y=x2在矩阵X对应的变换作用下得到的曲线方程
A2、已知二阶矩阵M=,α=
(1)求矩阵M的特征值域特征向量
(2)求M5α
B组(选修4-4:坐标系与参数方程)
B1、在平面直角坐标系xOy中,曲线C的参数方程为,(θ为参数)
(1)写出曲线C的直角坐标系方程
(2)若直线l经过点A(0,),倾斜角为45°,且与曲线C交于两M,N点,求MN的长.
B2、在平面直角坐标系xOy中,直线AB的参数方程为,(t为参数),以原点为极点,x正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=
2sin(θ+)(ρ≥0)
(1)求曲线C的参数方程
(2)设点M为曲线C上的动点,求点M与直线AB距离d的最小值.
11
