江苏省苏州市2008-2018学年高二(下)期末数学试卷(理科)分类汇编:圆锥曲线
文档属性
| 名称 | 江苏省苏州市2008-2018学年高二(下)期末数学试卷(理科)分类汇编:圆锥曲线 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 15:54:01 | ||
图片预览




文档简介
圆锥曲线
(苏州市2008-2009高二 理(下)期末)3.准线方程为的抛物线的标准方程为 。
(苏州市2008-2009高二 理(下)期末)20. 已知椭圆的短轴长为4,分别是椭圆的左,右焦点,直线与椭圆在第一象限内的交点为,的面积为,点是椭圆上的动点
(1)求椭圆的方程;
(2)若为钝角,求点的横坐标的取值范围;
(3)求的最小值。
(苏州市2009-2010高二 理(下)期末)3.?在平面直角坐标系xOy中,双曲线的右准线方程为? .
(苏州市2009-2010高二 理(下)期末)13.?椭圆(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若椭圆上存在点P,使得c?·?PF2?=a?·?PF1则该椭圆离心率的取值范围是??????????.
(苏州市2009-2010高二 理(下)期末)20.?(本小题满分16分)如图,椭圆的左顶点,右焦点分别为A,F,直线l的方程x=9,N为l上位于x轴上方的一点.
?(1)设线段AN与椭圆C交于点M,且点M是线段AN的中点,求证:MA⊥MF;
????(2)过三点A,F, N的圆与y轴交于P,Q两点,求线段PQ的长的取值范围
(苏州市2010-2011高二 理(下)期末)6.若双曲线8kx2-ky2=8的一个焦点为(0,3),则k的值为.
(苏州市2010-2011高二 理(下)期末)12.已知A,B,F分别是椭圆(a>b>0)的上、下顶点和右焦点,直线AF与椭圆的右准线交于点M.若直线MB∥x轴,则该椭圆的离心率e= .
(苏州市2010-2011高二 理(下)期末)14.将一块边界为椭圆的铁皮截成一块梯形铁皮.已知椭圆的长轴长为 4,短轴长为2.若以椭圆的短轴为梯形的一条底边,则梯形面积的最大值等于
(苏州市2010-2011高二 理(下)期末)20.(本小题满分16分)如图,在平面直角坐标系xOy中,椭圆E:(a>b>0)的离心率为,点B(0,)是椭圆E的上顶点,F1,F2分别是椭圆 E的左,右焦点.
(1)求椭圆 E的方程;
(2)已知M为椭圆E上的动点,若以点M为圆心,MF1为半径的圆与椭圆 E的右准线有公共点,求△ F1MF2面积的最大值;
(3)过点B作直线l1,l2,使l1⊥l2,设直线 l1,l2分别交椭圆 E于点P,Q,连接PQ,求证:直线PQ必经过y轴上的一个定点.
(苏州市2011-2012高二 理(下)期末)7.若双曲线的右焦点在抛物线的准线上,则实数m的值为 .
(苏州市2011-2012高二 理(下)期末)13.椭圆E:的左顶点为A,点B,C是椭圆E上的两个动点,若直线AB与AC的斜率乘积为定值,则动直线BC恒过定点的坐标为 .
(苏州市2011-2012高二 理(下)期末)20.(本小题满分16分)椭圆E:的左、右焦点分别为F1,F2,左、右顶点分别为A,B.
(1)若Rt△F1F2C的顶点C在椭圆E上的第一象限内,求点C的坐标;
(2)在定直线l:x m(m 2)上任取一点P(P不在轴上),线段PA交椭圆于点Q,若?PBQ始终为钝角,求实数m的取值范围.
(苏州市2012-2013高二 理(下)期末)2.抛物线y2 = 4x的准线方程为 .
(苏州市2012-2013高二 理(下)期末)11.过椭圆的焦点作垂直于x轴的直线交椭圆于A,B两点,若AB =,则双曲线的离心率为 .
(苏州市2012-2013高二 理(下)期末)16.(本小题满分14分)已知点M到双曲线的左、右焦点的距离之比为2︰3.
(1)求点M的轨迹方程;
(2)若点M的轨迹上有且仅有三个点到直线y = x + m的距离为4,求实数m的值.
(苏州市2012-2013高二 理(下)期末)20.(本小题满分16分)如图,点A( a,0),B(,)是椭圆上的两点,直线AB与y轴交于点C(0,1).
(1)求椭圆的方程;
(2)过点C任意作一条直线PQ与椭圆相交于P,Q,求PQ的取值范围.
(苏州市2013-2014高二 理(下)期末)5.在平面直角坐标系xOy中,设点p是抛物线x2=2y上位于第一象限的点,若点p到抛物线准线的距离为1,则点p的坐标为 .
(苏州市2013-2014高二 理(下)期末)12.椭圆c:(a>b>0),过定点A(1,2),椭圆的中心到准线的距离的最小值 .
(苏州市2013-2014高二 理(下)期末)13.已知A={(x,y)|y2=4x},B={(x,y)||x-a|+|y|≤6},若A∩B=?,则a的范围为___.
(苏州市2013-2014高二 理(下)期末)16.(本小题满分14分)在平面直角坐标系xOy中,已知双曲线(a>0)的一条渐近线方程为3x+2y=0,点A为双曲线C的右顶点,圆O的方程为x2+y2=1.
(1)求a的值;
(2)点M为平面内一动点,过M引圆O的切线MN(N为切点),若=,求动点M的轨迹方程.
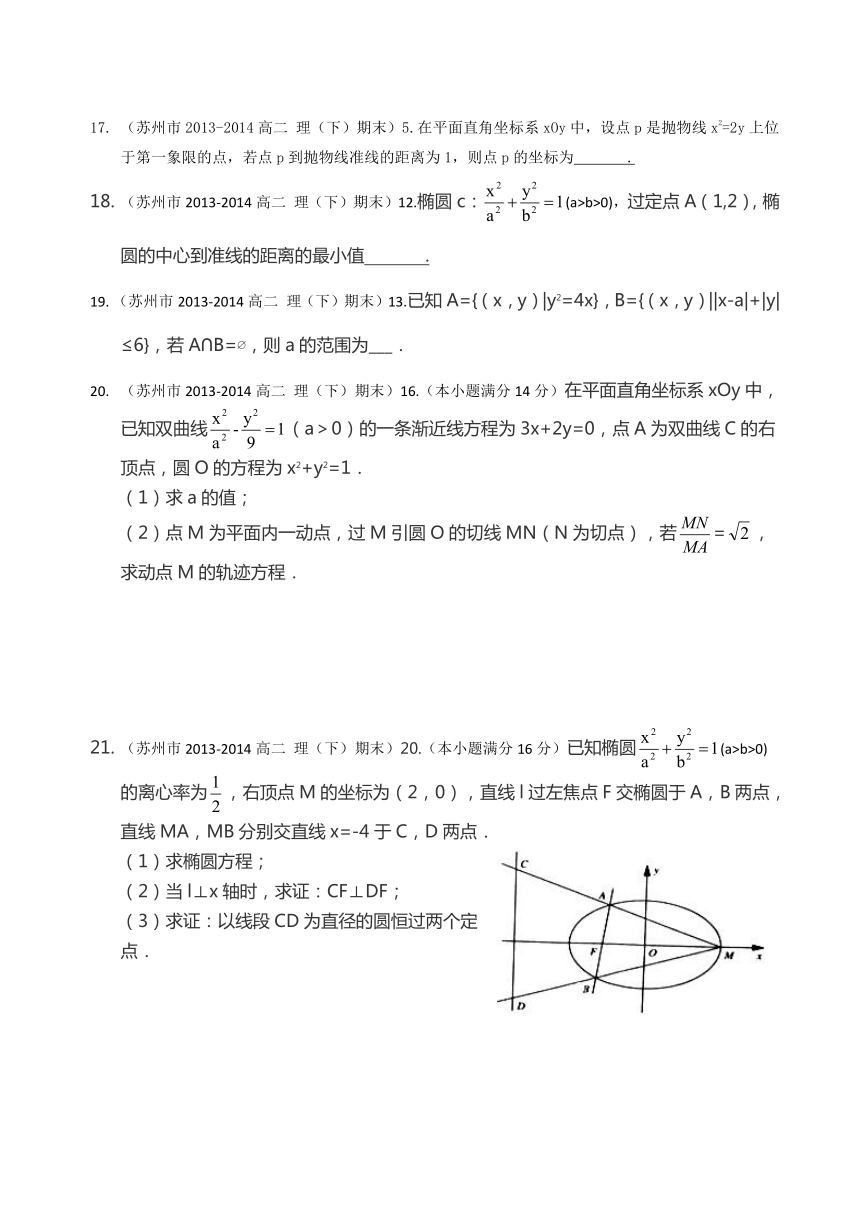
(苏州市2013-2014高二 理(下)期末)20.(本小题满分16分)已知椭圆(a>b>0)的离心率为,右顶点M的坐标为(2,0),直线l过左焦点F交椭圆于A,B两点,直线MA,MB分别交直线x=-4于C,D两点.
(1)求椭圆方程;
(2)当l⊥x轴时,求证:CF⊥DF;
(3)求证:以线段CD为直径的圆恒过两个定点.
(苏州市2014-2015高二 理(下)期末)5.在平面直角坐标系xoy中,已知抛物线x2 = ay 经过点,则点A 到抛物线的焦点的距离为 .
(苏州市2014-2015高二 理(下)期末)17.(本小题满分14 分)在平面直角坐标系xoy 中,已知圆心在第二象限,半径为 的圆C与直线y = x 相切于坐标原点O,椭圆与圆C 的一个交点到椭圆的两焦点的距离之和为10.
(1) 求圆C 的方程;
(2) 若圆C上存在一点Q(异于坐标原点),满足点Q 到椭圆右焦点F的距离等于OF的长,试求出
点Q的坐标.
(苏州市2014-2015高二 理(下)期末)19.(本小题满分16 分)在平面直角坐标系xoy中,已知双曲线的左、右顶点分别为是双曲线上不同的两个动点.
(1) 求直线A1P与A2Q交点的轨迹E的方程;
(2) 过坐标原点O作一条直线交轨迹E于A, B 两点,过点B作x轴的垂线,垂足为点C,连AC交
轨迹E于点D,求证:AB? BD.
(苏州市2015-2016(2017-2018)高二 理(下)期末)4.若双曲线(a>0)的离心率为2,则a等于 .
(苏州市2015-2016(2017-2018)高二 理(下)期末)11.已知点A(﹣3,﹣2)在抛物线C:x2=2py的准线上,过点A的直线与抛物线C在第二象限相切于点B,记抛物线C的焦点为F,则直线BF的斜率是 .
(苏州市2015-2016(2017-2018)高二 理(下)期末)14.若实数a,b满足a=+2,则a的最大值是 .
(苏州市2015-2016(2017-2018)高二 理(下)期末)19.如图,已知椭圆M:(a>b>0)的离心率为,且经过过点P(2,1).
(1)求椭圆M的标准方程;
(2)设点A(x1,y1),B(x2,y2)是椭圆M上异于顶点的任意两点,直线OA,OB的斜率分别为k1,k2,且k1k2=.
①求x12+x22的值;
②设点B关于x轴的对称点为C(点C,A不重合),试求直线AC的斜率.
(苏州市2016-2017高二 理(下)期末)3.在平面直角坐标系xOy中,双曲线-=1的离心率为.
(苏州市2016-2017高二 理(下)期末)9.在平面直角坐标系xOy中,过抛物线y2=4x的焦点F作弦AB,则●= .
(苏州市2016-2017高二 理(下)期末)19.在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0),其焦点到相应准线的距离为,离心率为.
(1)求椭圆C的标准方程;y1
(2)如图所示A,B是椭圆C上两点,且△AOB的面积为,设射线OA,OB的斜率分别为k1,k2
①求k1●k2的值.
②延长OA到P,使得OP=2OA,且PB交椭圆C于Q,求证为定值.
答案:
x2=-y
【答案】
(1)∵2b=4,∴b=2,①
由题意,设A(x,x)(x>0),则,②
AF1F2的面积为2,∴cx=2③,
由①②③得:a=2,椭圆C的方程为:.
设p(x,y),则 F1(-2,0),F2(2,0),
且∠F1PF2是钝角
?PF12+PF22<F1F22?(x+2)2+y2+(x-2)2+y2<32
?x2+y2<8?-<x<.
椭圆与y=x(x>0)解得A(-,),
自P作椭圆左准线的垂线,垂足为H,∵==,
左准线方程:x=-3,
∴PF1+PA即为:(PH+PA)
当A,P,H三点共线时,其和最小,
|PA|+|PB|的最小值为|AB|,
因点A到左准线的距离为:+3,
∴PF1+PA的最小值(+3)=6+.
x=
-1e1
由题意得A(-6,0),F(4,0),xN=9∴xM=
又M点在椭圆上,且在x轴上方,得yM=
∴MA=(-,-),MF=(,-)
∴MA·MF=-+=0
∴MA⊥MF
(2)设N(9,t),其中t>0,∵圆过A,F,N三点,
∴设该圆的方程为x2+y2+Dx+Ey+F=0,有
解得?D=2,E=?t?,F=?24
∴圆心为(?1,(t+)),半径r=25+(t+)2
∴|PQ|=2=,
∵t>0∴t+≥2=10,当且仅当t=,即t=5时取“=”
∴|PQ|≥2=6,
∴|PQ|的取值范围是[6,+∞)
-1
-4
(1,0)
20.解:(1)椭圆E中,a2 4,b2 1,c2 3,
F1(,0),F2(,0),A(2,0),B(2,0),设C(x,y).
① 若∠F2F1C 90°,则点C不在第一象限内,与条件矛盾,不成立. ……… 1分
② 若∠F1F2C 90°,将x ,代入椭圆E的方程,得y ?.
∵点C在第一象限内,∴C(,). ………………… 3分
③ 若∠F1CF2 90°,∴OC OF2 .则x2 + y2 3. ………………… 5分
又,∴x2 ,y2 .
∵点C在第一象限内,x 0,y 0,
∴,. 即C(,). ………………… 7分
(2)设,则直线AQ方程为:.
∴. ……………………………… 9分
,.
∵y0≠0时,又为钝角,∴.
∴. ……………………………… 12分
∵2 x0 2,∴.
∵,∴.∴. ……………………… 16分
x=-1.
解:(1)双曲线的左、右焦点为,.………1分
设点,则, 即. ……………3分
化简得点M的轨迹方程为. ……………7分
(2)点M的轨迹方程即为,
它表示以为圆心,12为半径的圆. ……………9分
因为圆上有且仅有三点到直线y = x + m的距离为4,
所以圆心到直线y = x + m的距离为8,即. ……………12分
解得 . ……………14分
解:(1)由B(,),C(0,1),得直线BC方程为.………… 2分
令y = 0,得x = 2,∴a = 2. ………… 3分
将B(,)代入椭圆方程,得.∴b2 = 2.
椭圆方程为. ………… 5分
(2)① 当PQ与x轴垂直时,PQ = ; ………… 6分
② 当PQ与x轴不垂直时,不妨设直线PQ:y = kx 1(k≥0),
代入椭圆方程x2 2y2 4 = 0,得x2 2(kx 1)2 4 = 0.
即 (2k2 1) x2 4kx 2 = 0. ………… 8分
设P(x1,y1),Q(x2,y2),则 .
则 | x1 x2 | = .PQ = . ………… 10分
=. ………… 12分
∵,在k =时取等号, ………… 14分
∴PQ2 = (8,9].则PQ. ………… 15分
由①,②得PQ的取值范围是. ………… 16分
(1,)
+2
(-∞,-6)
解:(1)∵双曲线
的渐近线方程为3x±ay=0,
由其中一条渐近线方程为3x+2y=0,
解得a=2.
(2)由(1)知双曲线方程为
∵点A为双曲线C的右顶点,∴A(2,0),
设M(x,y),∵圆O的方程为x2+y2=1,
∴N(cosθ,sinθ),0≤θ<π,
则(x-cosθ)2+(y-sinθ)2+1=x2+y2,
解得(x-cosθ)2+(y-sinθ)2=x2+y2-1,
∵=
∴=
∴=,
整理,得:x2+y2-8x+9=0.
∴动点M的轨迹方程为x2+y2-8x+9=0
(1)∵椭圆(a>b>0)的离心率为,右顶点M的坐标为(2,0),
∴= a=2,解得a=2,c=1,∴b2=4-1=3,
∴椭圆方程为
(2)证明:∵直线l过左焦点F(-1,0)交椭圆于A,B两点,l⊥x轴,
∴直线l的方程为x=-1,
联立,得A(-1,),B(-1,-),
∴直线MA:x+2y-2=0,联立x=-4;x+2y-2=0,得C(-4,3),
从而能证明CF⊥DF.
(3)设A(x1,y1),B(x2,y2),AB:x=my-1,代入椭圆方程,得(3m2+4)y2-6my-9=0,由此利用已知条件能证明以线段CD为直径的圆过x轴上的两个定点(-1,0)和(-7,0).
解:(1)设圆C的圆心为A(p,q),则圆C的方程为(x-p)2+(y-q)2=8
∵直线y=x与圆C相切于坐标原点O,?
∴O在圆C上,且直线OA垂直于直线y=x
于是有
由于点A(p,q)在第二象限,故p<0
所以圆C的方程为(x+2)2+(y-2)2=8;
(2)∵椭圆与圆C的一个交点到椭圆两焦点距离之和为10
∴2a=10a=5
故椭圆右焦点为F(4,0)
若圆C上存在异于原点的点Q(x0,y0)到椭圆右焦点F的距离等于线段OF的长,
则有|QF|=|OF|,于是
由于Q(x0,y0)在圆上,故有
解①和②得?
故圆C上存在满足条件的点。
由A1,A2为双曲线的左右顶点知,A1(- ,0),A2( ,0),
则A1P:y= (x+ ),A2Q:y= - (x- ),
两式相乘得y2= (x2-2),
因为点P(x0,y0)在双曲线上,所以 ,即 =,
所以y2=- (x2-2),即 x2 2 +y2=1,
故直线A1P与A2Q交点的轨迹E的方程为 +y2=1.(x≠± ,x≠0)
由(1)知,轨迹E的方程为 +y2=1.(x≠± ,x≠0)
设B(x1,y1),D(x2,y2),A(-x1,-y1).
因为点B和D都在曲线E上,所以+y12=1,+y22=1
两式相减得+(y1+y2)(y1-y2)=0,
所以KAD·KBD=·=-
又KAD=KAC==KAB
KAB·KBD=-1
所以AB⊥BD
1
20
解:(1)由题意可得e==, +=1,a2﹣b2=c2,
解得a=,b=,可得椭圆标准方程为+=1;
(2)①由题意可得k1k2==﹣,
即为x12x22=16y12y22,
又点A(x1,y1),B(x2,y2)是椭圆M上异于顶点的任意两点,
可得4y12=6﹣x12,4y22=6﹣x22,
即有x12x22=(6﹣x12)(6﹣x22),化简可得x12+x22=6;
②由题意可得C(x2,﹣y2),
由4y12=6﹣x12,4y22=6﹣x22,
可得y12+y22==,
由x12+x22=(x1﹣x2)2+2x1x2=6,
可得(x1﹣x2)2=6﹣2x1x2,
由y12+y22=(y1+y2)2﹣2y1y2=,
可得(y1+y2)2=+2y1y2=(3+4y1y2),
由=﹣,即x1x2=﹣4y1y2,
可得(x1﹣x2)2=6﹣2x1x2=6+8y1y2,
则直线AC的斜率为kAC==±=±.
-3
(苏州市2008-2009高二 理(下)期末)3.准线方程为的抛物线的标准方程为 。
(苏州市2008-2009高二 理(下)期末)20. 已知椭圆的短轴长为4,分别是椭圆的左,右焦点,直线与椭圆在第一象限内的交点为,的面积为,点是椭圆上的动点
(1)求椭圆的方程;
(2)若为钝角,求点的横坐标的取值范围;
(3)求的最小值。
(苏州市2009-2010高二 理(下)期末)3.?在平面直角坐标系xOy中,双曲线的右准线方程为? .
(苏州市2009-2010高二 理(下)期末)13.?椭圆(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若椭圆上存在点P,使得c?·?PF2?=a?·?PF1则该椭圆离心率的取值范围是??????????.
(苏州市2009-2010高二 理(下)期末)20.?(本小题满分16分)如图,椭圆的左顶点,右焦点分别为A,F,直线l的方程x=9,N为l上位于x轴上方的一点.
?(1)设线段AN与椭圆C交于点M,且点M是线段AN的中点,求证:MA⊥MF;
????(2)过三点A,F, N的圆与y轴交于P,Q两点,求线段PQ的长的取值范围
(苏州市2010-2011高二 理(下)期末)6.若双曲线8kx2-ky2=8的一个焦点为(0,3),则k的值为.
(苏州市2010-2011高二 理(下)期末)12.已知A,B,F分别是椭圆(a>b>0)的上、下顶点和右焦点,直线AF与椭圆的右准线交于点M.若直线MB∥x轴,则该椭圆的离心率e= .
(苏州市2010-2011高二 理(下)期末)14.将一块边界为椭圆的铁皮截成一块梯形铁皮.已知椭圆的长轴长为 4,短轴长为2.若以椭圆的短轴为梯形的一条底边,则梯形面积的最大值等于
(苏州市2010-2011高二 理(下)期末)20.(本小题满分16分)如图,在平面直角坐标系xOy中,椭圆E:(a>b>0)的离心率为,点B(0,)是椭圆E的上顶点,F1,F2分别是椭圆 E的左,右焦点.
(1)求椭圆 E的方程;
(2)已知M为椭圆E上的动点,若以点M为圆心,MF1为半径的圆与椭圆 E的右准线有公共点,求△ F1MF2面积的最大值;
(3)过点B作直线l1,l2,使l1⊥l2,设直线 l1,l2分别交椭圆 E于点P,Q,连接PQ,求证:直线PQ必经过y轴上的一个定点.
(苏州市2011-2012高二 理(下)期末)7.若双曲线的右焦点在抛物线的准线上,则实数m的值为 .
(苏州市2011-2012高二 理(下)期末)13.椭圆E:的左顶点为A,点B,C是椭圆E上的两个动点,若直线AB与AC的斜率乘积为定值,则动直线BC恒过定点的坐标为 .
(苏州市2011-2012高二 理(下)期末)20.(本小题满分16分)椭圆E:的左、右焦点分别为F1,F2,左、右顶点分别为A,B.
(1)若Rt△F1F2C的顶点C在椭圆E上的第一象限内,求点C的坐标;
(2)在定直线l:x m(m 2)上任取一点P(P不在轴上),线段PA交椭圆于点Q,若?PBQ始终为钝角,求实数m的取值范围.
(苏州市2012-2013高二 理(下)期末)2.抛物线y2 = 4x的准线方程为 .
(苏州市2012-2013高二 理(下)期末)11.过椭圆的焦点作垂直于x轴的直线交椭圆于A,B两点,若AB =,则双曲线的离心率为 .
(苏州市2012-2013高二 理(下)期末)16.(本小题满分14分)已知点M到双曲线的左、右焦点的距离之比为2︰3.
(1)求点M的轨迹方程;
(2)若点M的轨迹上有且仅有三个点到直线y = x + m的距离为4,求实数m的值.
(苏州市2012-2013高二 理(下)期末)20.(本小题满分16分)如图,点A( a,0),B(,)是椭圆上的两点,直线AB与y轴交于点C(0,1).
(1)求椭圆的方程;
(2)过点C任意作一条直线PQ与椭圆相交于P,Q,求PQ的取值范围.
(苏州市2013-2014高二 理(下)期末)5.在平面直角坐标系xOy中,设点p是抛物线x2=2y上位于第一象限的点,若点p到抛物线准线的距离为1,则点p的坐标为 .
(苏州市2013-2014高二 理(下)期末)12.椭圆c:(a>b>0),过定点A(1,2),椭圆的中心到准线的距离的最小值 .
(苏州市2013-2014高二 理(下)期末)13.已知A={(x,y)|y2=4x},B={(x,y)||x-a|+|y|≤6},若A∩B=?,则a的范围为___.
(苏州市2013-2014高二 理(下)期末)16.(本小题满分14分)在平面直角坐标系xOy中,已知双曲线(a>0)的一条渐近线方程为3x+2y=0,点A为双曲线C的右顶点,圆O的方程为x2+y2=1.
(1)求a的值;
(2)点M为平面内一动点,过M引圆O的切线MN(N为切点),若=,求动点M的轨迹方程.
(苏州市2013-2014高二 理(下)期末)20.(本小题满分16分)已知椭圆(a>b>0)的离心率为,右顶点M的坐标为(2,0),直线l过左焦点F交椭圆于A,B两点,直线MA,MB分别交直线x=-4于C,D两点.
(1)求椭圆方程;
(2)当l⊥x轴时,求证:CF⊥DF;
(3)求证:以线段CD为直径的圆恒过两个定点.
(苏州市2014-2015高二 理(下)期末)5.在平面直角坐标系xoy中,已知抛物线x2 = ay 经过点,则点A 到抛物线的焦点的距离为 .
(苏州市2014-2015高二 理(下)期末)17.(本小题满分14 分)在平面直角坐标系xoy 中,已知圆心在第二象限,半径为 的圆C与直线y = x 相切于坐标原点O,椭圆与圆C 的一个交点到椭圆的两焦点的距离之和为10.
(1) 求圆C 的方程;
(2) 若圆C上存在一点Q(异于坐标原点),满足点Q 到椭圆右焦点F的距离等于OF的长,试求出
点Q的坐标.
(苏州市2014-2015高二 理(下)期末)19.(本小题满分16 分)在平面直角坐标系xoy中,已知双曲线的左、右顶点分别为是双曲线上不同的两个动点.
(1) 求直线A1P与A2Q交点的轨迹E的方程;
(2) 过坐标原点O作一条直线交轨迹E于A, B 两点,过点B作x轴的垂线,垂足为点C,连AC交
轨迹E于点D,求证:AB? BD.
(苏州市2015-2016(2017-2018)高二 理(下)期末)4.若双曲线(a>0)的离心率为2,则a等于 .
(苏州市2015-2016(2017-2018)高二 理(下)期末)11.已知点A(﹣3,﹣2)在抛物线C:x2=2py的准线上,过点A的直线与抛物线C在第二象限相切于点B,记抛物线C的焦点为F,则直线BF的斜率是 .
(苏州市2015-2016(2017-2018)高二 理(下)期末)14.若实数a,b满足a=+2,则a的最大值是 .
(苏州市2015-2016(2017-2018)高二 理(下)期末)19.如图,已知椭圆M:(a>b>0)的离心率为,且经过过点P(2,1).
(1)求椭圆M的标准方程;
(2)设点A(x1,y1),B(x2,y2)是椭圆M上异于顶点的任意两点,直线OA,OB的斜率分别为k1,k2,且k1k2=.
①求x12+x22的值;
②设点B关于x轴的对称点为C(点C,A不重合),试求直线AC的斜率.
(苏州市2016-2017高二 理(下)期末)3.在平面直角坐标系xOy中,双曲线-=1的离心率为.
(苏州市2016-2017高二 理(下)期末)9.在平面直角坐标系xOy中,过抛物线y2=4x的焦点F作弦AB,则●= .
(苏州市2016-2017高二 理(下)期末)19.在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0),其焦点到相应准线的距离为,离心率为.
(1)求椭圆C的标准方程;y1
(2)如图所示A,B是椭圆C上两点,且△AOB的面积为,设射线OA,OB的斜率分别为k1,k2
①求k1●k2的值.
②延长OA到P,使得OP=2OA,且PB交椭圆C于Q,求证为定值.
答案:
x2=-y
【答案】
(1)∵2b=4,∴b=2,①
由题意,设A(x,x)(x>0),则,②
AF1F2的面积为2,∴cx=2③,
由①②③得:a=2,椭圆C的方程为:.
设p(x,y),则 F1(-2,0),F2(2,0),
且∠F1PF2是钝角
?PF12+PF22<F1F22?(x+2)2+y2+(x-2)2+y2<32
?x2+y2<8?-<x<.
椭圆与y=x(x>0)解得A(-,),
自P作椭圆左准线的垂线,垂足为H,∵==,
左准线方程:x=-3,
∴PF1+PA即为:(PH+PA)
当A,P,H三点共线时,其和最小,
|PA|+|PB|的最小值为|AB|,
因点A到左准线的距离为:+3,
∴PF1+PA的最小值(+3)=6+.
x=
-1e1
由题意得A(-6,0),F(4,0),xN=9∴xM=
又M点在椭圆上,且在x轴上方,得yM=
∴MA=(-,-),MF=(,-)
∴MA·MF=-+=0
∴MA⊥MF
(2)设N(9,t),其中t>0,∵圆过A,F,N三点,
∴设该圆的方程为x2+y2+Dx+Ey+F=0,有
解得?D=2,E=?t?,F=?24
∴圆心为(?1,(t+)),半径r=25+(t+)2
∴|PQ|=2=,
∵t>0∴t+≥2=10,当且仅当t=,即t=5时取“=”
∴|PQ|≥2=6,
∴|PQ|的取值范围是[6,+∞)
-1
-4
(1,0)
20.解:(1)椭圆E中,a2 4,b2 1,c2 3,
F1(,0),F2(,0),A(2,0),B(2,0),设C(x,y).
① 若∠F2F1C 90°,则点C不在第一象限内,与条件矛盾,不成立. ……… 1分
② 若∠F1F2C 90°,将x ,代入椭圆E的方程,得y ?.
∵点C在第一象限内,∴C(,). ………………… 3分
③ 若∠F1CF2 90°,∴OC OF2 .则x2 + y2 3. ………………… 5分
又,∴x2 ,y2 .
∵点C在第一象限内,x 0,y 0,
∴,. 即C(,). ………………… 7分
(2)设,则直线AQ方程为:.
∴. ……………………………… 9分
,.
∵y0≠0时,又为钝角,∴.
∴. ……………………………… 12分
∵2 x0 2,∴.
∵,∴.∴. ……………………… 16分
x=-1.
解:(1)双曲线的左、右焦点为,.………1分
设点,则, 即. ……………3分
化简得点M的轨迹方程为. ……………7分
(2)点M的轨迹方程即为,
它表示以为圆心,12为半径的圆. ……………9分
因为圆上有且仅有三点到直线y = x + m的距离为4,
所以圆心到直线y = x + m的距离为8,即. ……………12分
解得 . ……………14分
解:(1)由B(,),C(0,1),得直线BC方程为.………… 2分
令y = 0,得x = 2,∴a = 2. ………… 3分
将B(,)代入椭圆方程,得.∴b2 = 2.
椭圆方程为. ………… 5分
(2)① 当PQ与x轴垂直时,PQ = ; ………… 6分
② 当PQ与x轴不垂直时,不妨设直线PQ:y = kx 1(k≥0),
代入椭圆方程x2 2y2 4 = 0,得x2 2(kx 1)2 4 = 0.
即 (2k2 1) x2 4kx 2 = 0. ………… 8分
设P(x1,y1),Q(x2,y2),则 .
则 | x1 x2 | = .PQ = . ………… 10分
=. ………… 12分
∵,在k =时取等号, ………… 14分
∴PQ2 = (8,9].则PQ. ………… 15分
由①,②得PQ的取值范围是. ………… 16分
(1,)
+2
(-∞,-6)
解:(1)∵双曲线
的渐近线方程为3x±ay=0,
由其中一条渐近线方程为3x+2y=0,
解得a=2.
(2)由(1)知双曲线方程为
∵点A为双曲线C的右顶点,∴A(2,0),
设M(x,y),∵圆O的方程为x2+y2=1,
∴N(cosθ,sinθ),0≤θ<π,
则(x-cosθ)2+(y-sinθ)2+1=x2+y2,
解得(x-cosθ)2+(y-sinθ)2=x2+y2-1,
∵=
∴=
∴=,
整理,得:x2+y2-8x+9=0.
∴动点M的轨迹方程为x2+y2-8x+9=0
(1)∵椭圆(a>b>0)的离心率为,右顶点M的坐标为(2,0),
∴= a=2,解得a=2,c=1,∴b2=4-1=3,
∴椭圆方程为
(2)证明:∵直线l过左焦点F(-1,0)交椭圆于A,B两点,l⊥x轴,
∴直线l的方程为x=-1,
联立,得A(-1,),B(-1,-),
∴直线MA:x+2y-2=0,联立x=-4;x+2y-2=0,得C(-4,3),
从而能证明CF⊥DF.
(3)设A(x1,y1),B(x2,y2),AB:x=my-1,代入椭圆方程,得(3m2+4)y2-6my-9=0,由此利用已知条件能证明以线段CD为直径的圆过x轴上的两个定点(-1,0)和(-7,0).
解:(1)设圆C的圆心为A(p,q),则圆C的方程为(x-p)2+(y-q)2=8
∵直线y=x与圆C相切于坐标原点O,?
∴O在圆C上,且直线OA垂直于直线y=x
于是有
由于点A(p,q)在第二象限,故p<0
所以圆C的方程为(x+2)2+(y-2)2=8;
(2)∵椭圆与圆C的一个交点到椭圆两焦点距离之和为10
∴2a=10a=5
故椭圆右焦点为F(4,0)
若圆C上存在异于原点的点Q(x0,y0)到椭圆右焦点F的距离等于线段OF的长,
则有|QF|=|OF|,于是
由于Q(x0,y0)在圆上,故有
解①和②得?
故圆C上存在满足条件的点。
由A1,A2为双曲线的左右顶点知,A1(- ,0),A2( ,0),
则A1P:y= (x+ ),A2Q:y= - (x- ),
两式相乘得y2= (x2-2),
因为点P(x0,y0)在双曲线上,所以 ,即 =,
所以y2=- (x2-2),即 x2 2 +y2=1,
故直线A1P与A2Q交点的轨迹E的方程为 +y2=1.(x≠± ,x≠0)
由(1)知,轨迹E的方程为 +y2=1.(x≠± ,x≠0)
设B(x1,y1),D(x2,y2),A(-x1,-y1).
因为点B和D都在曲线E上,所以+y12=1,+y22=1
两式相减得+(y1+y2)(y1-y2)=0,
所以KAD·KBD=·=-
又KAD=KAC==KAB
KAB·KBD=-1
所以AB⊥BD
1
20
解:(1)由题意可得e==, +=1,a2﹣b2=c2,
解得a=,b=,可得椭圆标准方程为+=1;
(2)①由题意可得k1k2==﹣,
即为x12x22=16y12y22,
又点A(x1,y1),B(x2,y2)是椭圆M上异于顶点的任意两点,
可得4y12=6﹣x12,4y22=6﹣x22,
即有x12x22=(6﹣x12)(6﹣x22),化简可得x12+x22=6;
②由题意可得C(x2,﹣y2),
由4y12=6﹣x12,4y22=6﹣x22,
可得y12+y22==,
由x12+x22=(x1﹣x2)2+2x1x2=6,
可得(x1﹣x2)2=6﹣2x1x2,
由y12+y22=(y1+y2)2﹣2y1y2=,
可得(y1+y2)2=+2y1y2=(3+4y1y2),
由=﹣,即x1x2=﹣4y1y2,
可得(x1﹣x2)2=6﹣2x1x2=6+8y1y2,
则直线AC的斜率为kAC==±=±.
-3
