人教A版高中数学必修五 第一章解三角形 章末总结(31张PPT)
文档属性
| 名称 | 人教A版高中数学必修五 第一章解三角形 章末总结(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-10 00:00:00 | ||
图片预览











文档简介
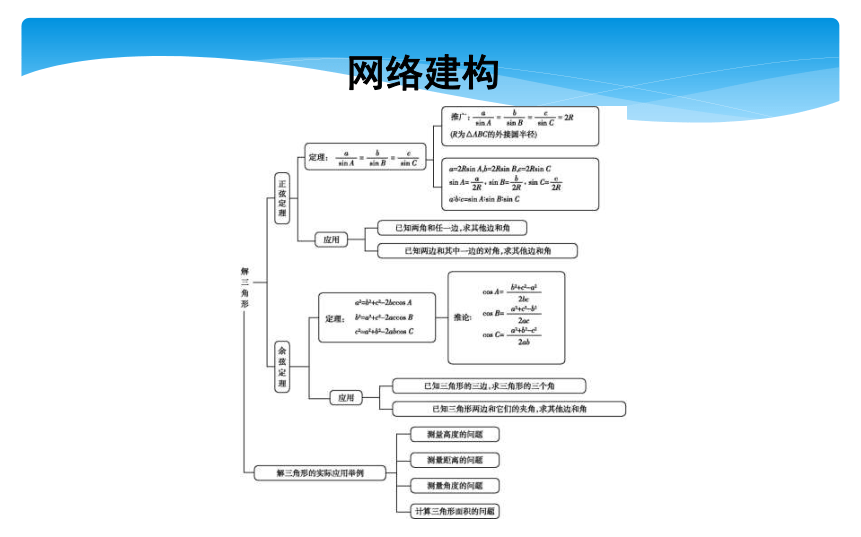
课件31张PPT。章末总结网络建构主题串讲一、利用正、余弦定理解三角形(1)证明:sin Asin B=sin C;(2)若b2+c2-a2= bc,求tan B.规律方法 应用正弦、余弦定理的解题技巧(3)已知两边和夹角或已知三边可利用余弦定理求解.
(4)灵活利用式子的特点转化:如出现a2+b2-c2=λab形式用余弦定理,等式两边是关于边或角的正弦的齐次式用正弦定理.二、利用正、余弦定理判定三角形的形状
【典例2】 (1)在△ABC中,角A,B,C所对的边分别为a,b,c,若(A)钝角三角形 (B)直角三角形
(C)锐角三角形 (D)等边三角形(A)等边三角形
(B)直角三角形
(C)等腰三角形或直角三角形
(D)等腰直角三角形规律方法 (1)判断三角形形状的方法
①化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
②化角:通过三角恒等变换,得出内角的关系,从而判断三角形的形状,此时要注意应用A+B+C=π这个结论.
(2)求解几何计算问题要注意
①根据已知的边角画出图形并在图中标示;
②选择在某个三角形中运用正弦定理或余弦定理.
另外,在判断三角形的形状时一定要注意解是否唯一,并注重挖掘隐含条件.另外,在变形过程中要注意角A,B,C的范围对三角函数值的影响,在等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.三、与三角形面积有关的问题【典例3】 已知a,b,c分别为△ABC三个内角A,B,C的对边,满足bcos C+
bsin C-a-c=0.
(1)求角B的值;(2)若a=2,且AC边上的中线BD长为 ,求△ABC的面积.(2)在涉及三角形面积时,常常借助正弦定理或余弦定理进行边和角的转化.四、三角形中的取值范围
【典例4】 设△ABC的内角A,B,C的对边分别为a,b,c,a=btan A,且B为钝角.
(1)证明:B-A= ;(2)求sin A+sin C的取值范围.规律方法 解三角形问题中,求解某个量(式子)的取值范围是命题的热点,其主要解决思路是:要建立所求量(式子)与已知角或边的关系,然后把角或边作为自变量,所求量(式子)的值作为函数值,转化为函数关系,将原问题转化为求函数的值域问题.这里要利用条件中的范围限制,以及三角形自身范围限制,要尽量把角或边的范围(也就是函数的定义域)找完善,避免结果的范围过大.
涉及求范围的问题,一定要搞清已知变量的范围,利用已知的范围进行求解,已知边的范围求角的范围时可以利用余弦定理进行转化.五、利用正、余弦定理解决实际应用问题(1)求该船的行驶速度(单位:海里/小时);(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.规律方法 解决实际问题的关键是根据问题所提供的信息画出图形,建立数学模型,通过解三角形,得到距离或角度.本题的限制区域是一个圆形,其实质是判断直线与圆的位置关系,所以要比较圆的半径与圆心到直线的距离的大小.六、易错类型
【典例6】 设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围.错因分析:产生以上错解的原因是在错解中求得的a> 不是2a+1,a,2a-1表示三角形三边的充要条件.如当a=1时,a+(2a-1)<2a+1,此时就不能作为三角形的三边.误区警示 (1)解题时,易忽略三角形的三边应满足两边之和大于第三边,而使某些字母的范围变大.
(2)本题实质上是求2a+1,a,2a-1能构成钝角三角形三边的充要条件,除了要保证三边长均为正数外,还应满足两边之和大于第三边、最大边所对角的余弦值为负数.真题体验B 2.(2017·山东卷,理9)在△ABC中,角A,B,C的对边分别为a,b,c.若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin Acos C+cos Asin C,则下列等式成立的是( )
(A)a=2b (B)b=2a
(C)A=2B (D)B=2A解析:因为等式右边=sin Acos C+(sin Acos C+cos Acos C)
=sin Acos C+sin(A+C)
=sin Acos C+sin B,
等式左边=sin B+2sin Bcos C,
所以sin B+2sin Bcos C=sin Acos C+sin B.
由cos C>0,得sin A=2sin B,
根据正弦定理,得a=2b,故选A.A3.(2017·全国Ⅲ卷,文15)△ABC的内角A,B,C的对边分别为a,b,c.已知C=60°,b= ,c=3,则A= .?答案:75°4.(2017·浙江卷,14)已知△ABC,AB=AC=4,BC=2.点D为AB延长线上一点,
BD=2,连接CD,则△BDC的面积是 ,cos∠BDC= .?5.(2017·天津卷,文15)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asin A=4bsin B,ac= (a2-b2-c2).
(1)求cos A的值;(2)求sin(2B-A)的值.(1)求c;(2)设D为BC边上一点,且AD⊥AC,求△ABD的面积.点击进入 检测试题谢谢观赏!
(4)灵活利用式子的特点转化:如出现a2+b2-c2=λab形式用余弦定理,等式两边是关于边或角的正弦的齐次式用正弦定理.二、利用正、余弦定理判定三角形的形状
【典例2】 (1)在△ABC中,角A,B,C所对的边分别为a,b,c,若
(C)锐角三角形 (D)等边三角形(A)等边三角形
(B)直角三角形
(C)等腰三角形或直角三角形
(D)等腰直角三角形规律方法 (1)判断三角形形状的方法
①化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
②化角:通过三角恒等变换,得出内角的关系,从而判断三角形的形状,此时要注意应用A+B+C=π这个结论.
(2)求解几何计算问题要注意
①根据已知的边角画出图形并在图中标示;
②选择在某个三角形中运用正弦定理或余弦定理.
另外,在判断三角形的形状时一定要注意解是否唯一,并注重挖掘隐含条件.另外,在变形过程中要注意角A,B,C的范围对三角函数值的影响,在等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.三、与三角形面积有关的问题【典例3】 已知a,b,c分别为△ABC三个内角A,B,C的对边,满足bcos C+
bsin C-a-c=0.
(1)求角B的值;(2)若a=2,且AC边上的中线BD长为 ,求△ABC的面积.(2)在涉及三角形面积时,常常借助正弦定理或余弦定理进行边和角的转化.四、三角形中的取值范围
【典例4】 设△ABC的内角A,B,C的对边分别为a,b,c,a=btan A,且B为钝角.
(1)证明:B-A= ;(2)求sin A+sin C的取值范围.规律方法 解三角形问题中,求解某个量(式子)的取值范围是命题的热点,其主要解决思路是:要建立所求量(式子)与已知角或边的关系,然后把角或边作为自变量,所求量(式子)的值作为函数值,转化为函数关系,将原问题转化为求函数的值域问题.这里要利用条件中的范围限制,以及三角形自身范围限制,要尽量把角或边的范围(也就是函数的定义域)找完善,避免结果的范围过大.
涉及求范围的问题,一定要搞清已知变量的范围,利用已知的范围进行求解,已知边的范围求角的范围时可以利用余弦定理进行转化.五、利用正、余弦定理解决实际应用问题(1)求该船的行驶速度(单位:海里/小时);(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.规律方法 解决实际问题的关键是根据问题所提供的信息画出图形,建立数学模型,通过解三角形,得到距离或角度.本题的限制区域是一个圆形,其实质是判断直线与圆的位置关系,所以要比较圆的半径与圆心到直线的距离的大小.六、易错类型
【典例6】 设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围.错因分析:产生以上错解的原因是在错解中求得的a> 不是2a+1,a,2a-1表示三角形三边的充要条件.如当a=1时,a+(2a-1)<2a+1,此时就不能作为三角形的三边.误区警示 (1)解题时,易忽略三角形的三边应满足两边之和大于第三边,而使某些字母的范围变大.
(2)本题实质上是求2a+1,a,2a-1能构成钝角三角形三边的充要条件,除了要保证三边长均为正数外,还应满足两边之和大于第三边、最大边所对角的余弦值为负数.真题体验B 2.(2017·山东卷,理9)在△ABC中,角A,B,C的对边分别为a,b,c.若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin Acos C+cos Asin C,则下列等式成立的是( )
(A)a=2b (B)b=2a
(C)A=2B (D)B=2A解析:因为等式右边=sin Acos C+(sin Acos C+cos Acos C)
=sin Acos C+sin(A+C)
=sin Acos C+sin B,
等式左边=sin B+2sin Bcos C,
所以sin B+2sin Bcos C=sin Acos C+sin B.
由cos C>0,得sin A=2sin B,
根据正弦定理,得a=2b,故选A.A3.(2017·全国Ⅲ卷,文15)△ABC的内角A,B,C的对边分别为a,b,c.已知C=60°,b= ,c=3,则A= .?答案:75°4.(2017·浙江卷,14)已知△ABC,AB=AC=4,BC=2.点D为AB延长线上一点,
BD=2,连接CD,则△BDC的面积是 ,cos∠BDC= .?5.(2017·天津卷,文15)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asin A=4bsin B,ac= (a2-b2-c2).
(1)求cos A的值;(2)求sin(2B-A)的值.(1)求c;(2)设D为BC边上一点,且AD⊥AC,求△ABD的面积.点击进入 检测试题谢谢观赏!
