初三数学专题——旋转相似讲义(含解析)
文档属性
| 名称 | 初三数学专题——旋转相似讲义(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 400.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 22:00:25 | ||
图片预览

文档简介
专题:旋转相似
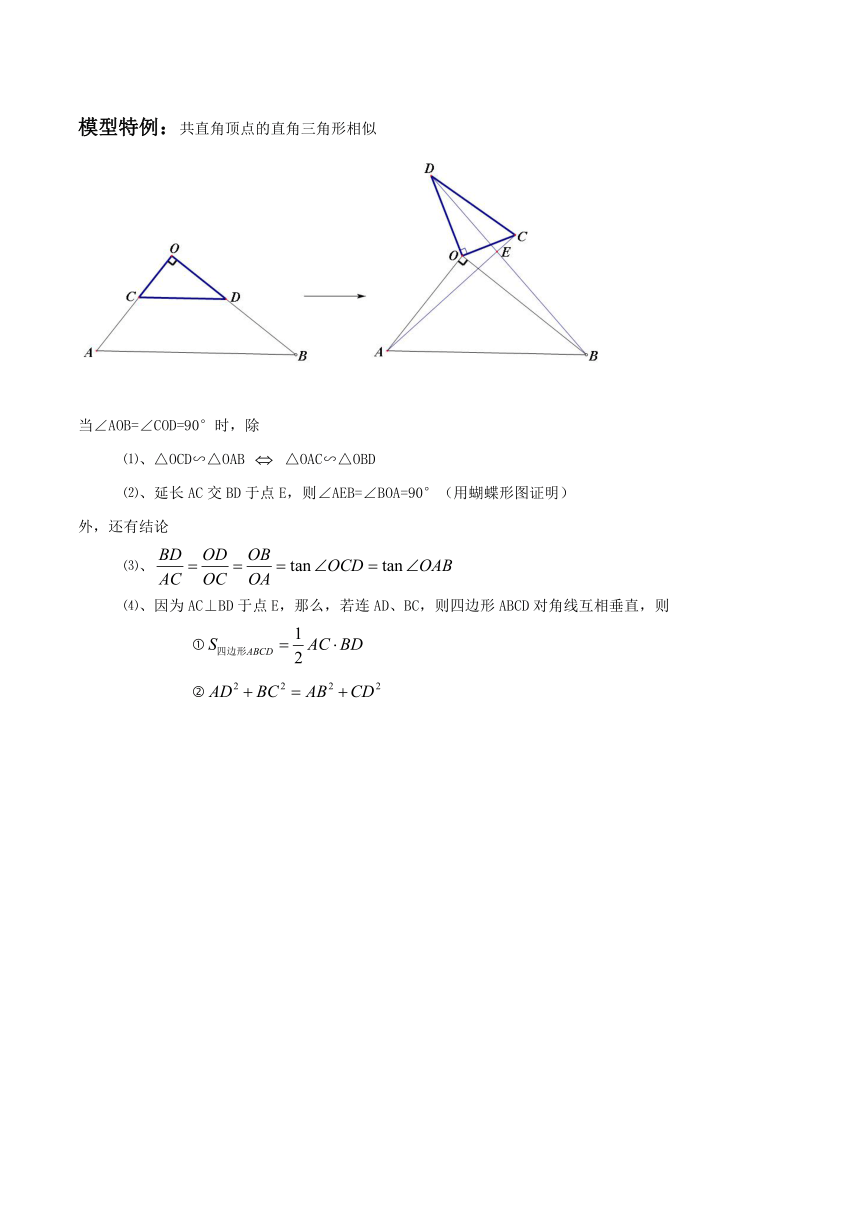
模型:手拉手相似模型,旋转相似成双对。
条件:CD∥AB(本质即为△OCD∽△OAB),将△OCD绕点O旋转到图1和图2的位置。
结论:⑴、△OCD∽△OAB △OAC∽△OBD。即连接对应点所得的一对新三角形相似。
⑵、延长AC交BD于点E,则∠AEB=∠BOA(用蝴蝶形图证明)(能得到点A、O、E、B四点共圆)
模型特例:共直角顶点的直角三角形相似
当∠AOB=∠COD=90°时,除
⑴、△OCD∽△OAB △OAC∽△OBD
⑵、延长AC交BD于点E,则∠AEB=∠BOA=90°(用蝴蝶形图证明)
外,还有结论
⑶、
⑷、因为AC⊥BD于点E,那么,若连AD、BC,则四边形ABCD对角线互相垂直,则
例题讲解
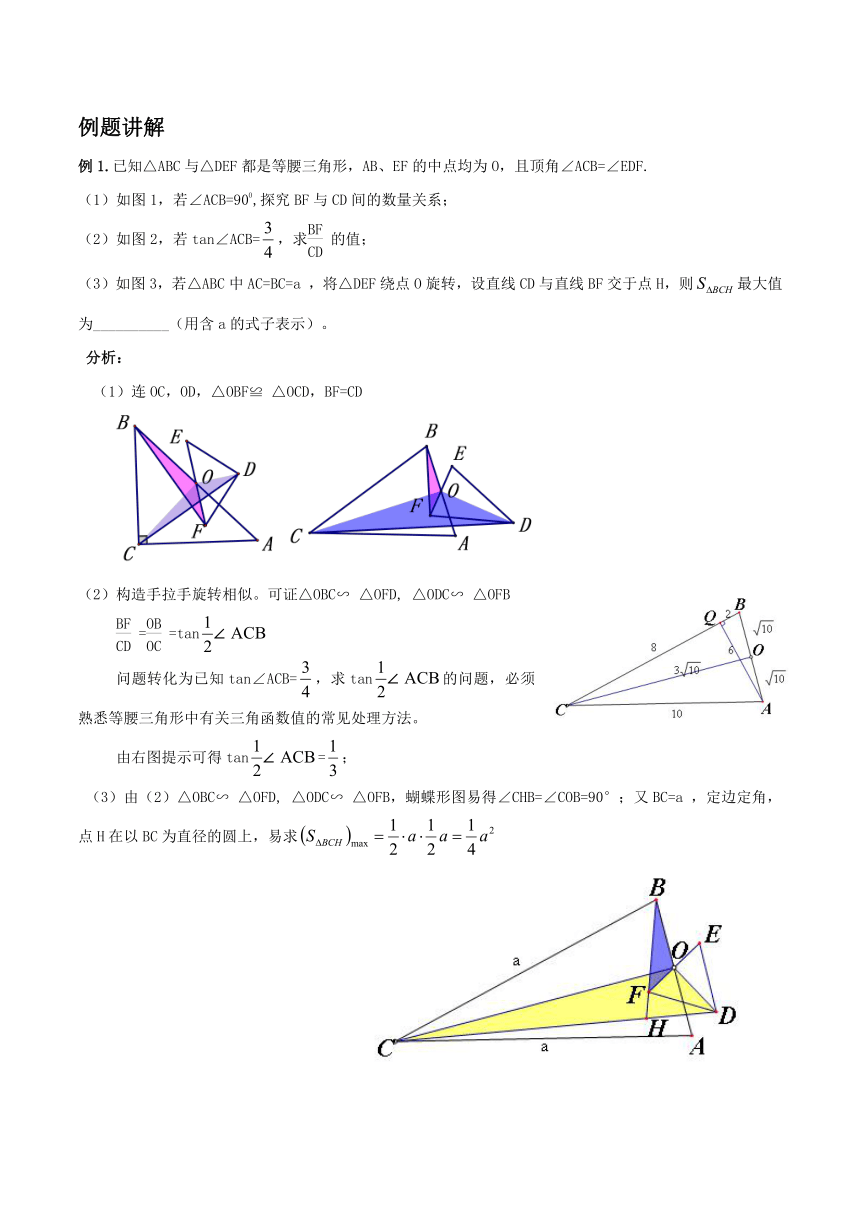
例1.已知△ABC与△DEF都是等腰三角形,AB、EF的中点均为O,且顶角∠ACB=∠EDF.
(1)如图1,若∠ACB=900,探究BF与CD间的数量关系;
(2)如图2,若tan∠ACB=,求的值;
(3)如图3,若△ABC中AC=BC=a ,将△DEF绕点O旋转,设直线CD与直线BF交于点H,则最大值为__________(用含a的式子表示)。
分析:
(1)连OC,OD,△OBF≌ △OCD,BF=CD
(2)构造手拉手旋转相似。可证△OBC∽ △OFD, △ODC∽ △OFB
==tan
问题转化为已知tan∠ACB=,求tan的问题,必须熟悉等腰三角形中有关三角函数值的常见处理方法。
由右图提示可得tan=;
(3)由(2)△OBC∽ △OFD, △ODC∽ △OFB,蝴蝶形图易得∠CHB=∠COB=90°;又BC=a ,定边定角,点H在以BC为直径的圆上,易求
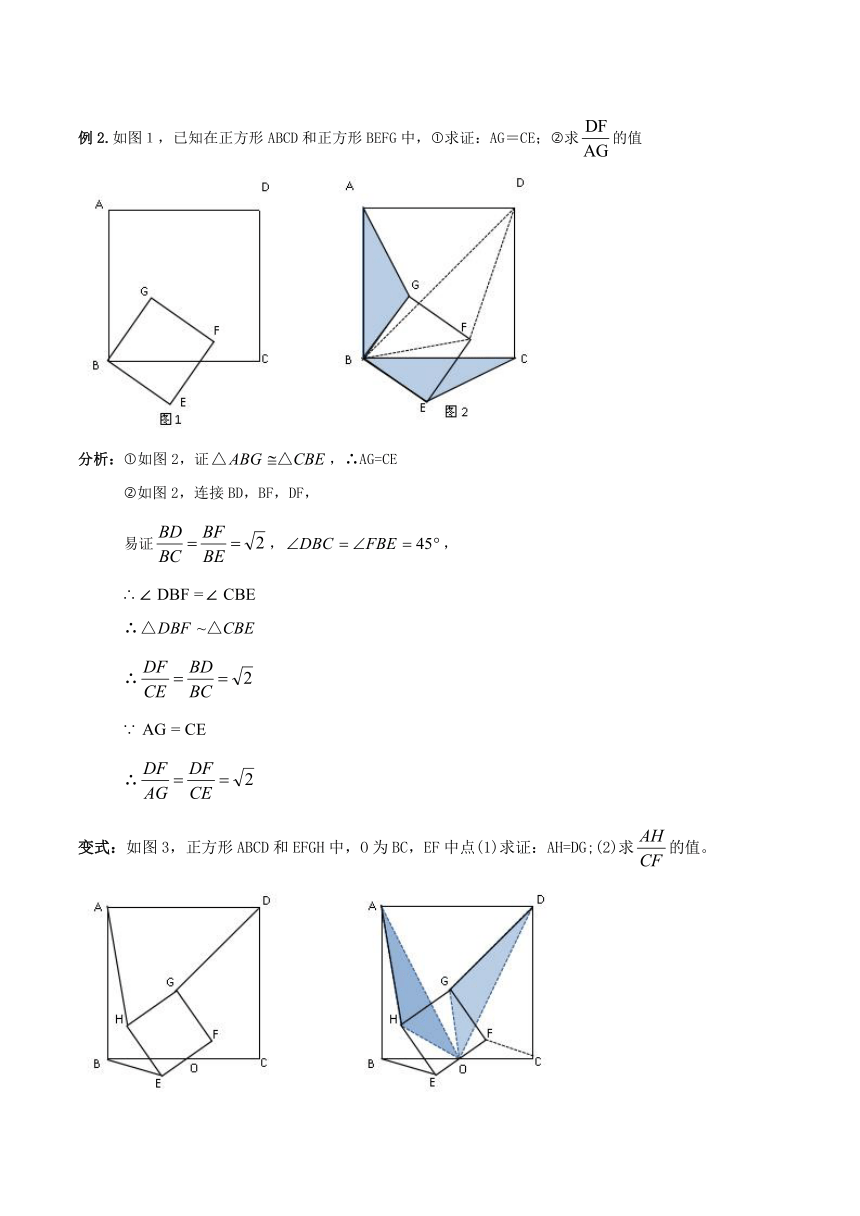
例2.如图1,已知在正方形ABCD和正方形BEFG中,求证:AG=CE;求的值
分析:如图2,证,∴AG=CE
如图2,连接BD,BF,DF,
易证,,
∴
∴
∴
变式:如图3,正方形ABCD和EFGH中,O为BC,EF中点(1)求证:AH=DG;(2)求的值。
分析:(1)连接
易证:
例3.如图,∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长。
分析:
连接BE,由基本图形易得
可证△ACD∽△BCE,AD= EQ \F(, 3 )BE,∠BAE=90°
在Rt△ABE作,由勾股定理求得BE=10
则AD= EQ \F(10, 3 )
练习1.如图,点A是△DBC内一点,求BD得长。
分析:构造旋转相似,由基本图形可得出以下几种方法,求出BD=10.
练习2.如图,在△ABC中,∠ACB=90°,BC=2AC,F、G分别为AC、BC的中点,将△CFG绕点C顺时针旋转,直线AF与直线BG交于点I.
(1) 求证:AF⊥BG;
(2) 当旋转角小于90°时,求的值;
(3) 若AC=4,直接写出△ACI面积的最大值___________.
分析:
(3)需分析出I点轨迹,由A、C、I、B四点共圆可得∠AIC=∠ABC,又AC=4,定边定角得I轨迹为圆弧。
练习3.将等腰Rt△ABC和等腰Rt△ADE按图1方式放置,∠A=90°,AD边与AB边重合,AB=2AD=4.将△ADE绕点A逆时针旋转(旋转角不超过180°),BD的延长线交直线CE于点P.
(1)如图2,BD与CE的数量关系是___________,位置关系是___________;
(2)在旋转的过程中,当AD⊥BD时,求CP的长;
(3)当点D落在BA的延长线上时,求点P所经过的路径的长.
分析:
(1)BD=CE BD⊥CE
(2)∵BD⊥CE,AD⊥BD,∴∠ADP=∠DPE=90°
又∠DAE=90°,AD=AE,∴四边形ADPE为正方形
∵AB=2AD=4,∴PE=AD=2
∴CE=BD==2
∴CP=2-2
(3)取BC中点O,连接OA、OP
∵在旋转过程中,BD⊥CE,∴∠BPC=90°
∴OP= BC=2
∴点P的运动路径是以O为圆心、半径为2的一段圆弧
即△ABC外接圆的一部分
则∠AOP=2∠ABP
易知点D在以A为圆心、半径为2的半圆上运动
当BP与半圆A相切于点D时,∠ABP最大,从而∠AOP最大
∵AD= AB,∴∠ABP=30°,∴∠AOP=60°
即当△ADE从初始位置旋转60°时,点P沿圆弧从A点运动到∠AOP=60°
当△ADE继续旋转,直至点D落在BA的延长线上时,∠ABP=0°,∠AOP=0°
∴点P从∠AOP=60°处又回到A点
∴点P所经过的路径的长为:2×=
A
E
D
B
C
A
E
D
B
C
A
E
D
B
C
A
E
B
C
图1
图2
D
A
D
B
C
E
P
A
E
B
C
D
O
P
模型:手拉手相似模型,旋转相似成双对。
条件:CD∥AB(本质即为△OCD∽△OAB),将△OCD绕点O旋转到图1和图2的位置。
结论:⑴、△OCD∽△OAB △OAC∽△OBD。即连接对应点所得的一对新三角形相似。
⑵、延长AC交BD于点E,则∠AEB=∠BOA(用蝴蝶形图证明)(能得到点A、O、E、B四点共圆)
模型特例:共直角顶点的直角三角形相似
当∠AOB=∠COD=90°时,除
⑴、△OCD∽△OAB △OAC∽△OBD
⑵、延长AC交BD于点E,则∠AEB=∠BOA=90°(用蝴蝶形图证明)
外,还有结论
⑶、
⑷、因为AC⊥BD于点E,那么,若连AD、BC,则四边形ABCD对角线互相垂直,则
例题讲解
例1.已知△ABC与△DEF都是等腰三角形,AB、EF的中点均为O,且顶角∠ACB=∠EDF.
(1)如图1,若∠ACB=900,探究BF与CD间的数量关系;
(2)如图2,若tan∠ACB=,求的值;
(3)如图3,若△ABC中AC=BC=a ,将△DEF绕点O旋转,设直线CD与直线BF交于点H,则最大值为__________(用含a的式子表示)。
分析:
(1)连OC,OD,△OBF≌ △OCD,BF=CD
(2)构造手拉手旋转相似。可证△OBC∽ △OFD, △ODC∽ △OFB
==tan
问题转化为已知tan∠ACB=,求tan的问题,必须熟悉等腰三角形中有关三角函数值的常见处理方法。
由右图提示可得tan=;
(3)由(2)△OBC∽ △OFD, △ODC∽ △OFB,蝴蝶形图易得∠CHB=∠COB=90°;又BC=a ,定边定角,点H在以BC为直径的圆上,易求
例2.如图1,已知在正方形ABCD和正方形BEFG中,求证:AG=CE;求的值
分析:如图2,证,∴AG=CE
如图2,连接BD,BF,DF,
易证,,
∴
∴
∴
变式:如图3,正方形ABCD和EFGH中,O为BC,EF中点(1)求证:AH=DG;(2)求的值。
分析:(1)连接
易证:
例3.如图,∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长。
分析:
连接BE,由基本图形易得
可证△ACD∽△BCE,AD= EQ \F(, 3 )BE,∠BAE=90°
在Rt△ABE作,由勾股定理求得BE=10
则AD= EQ \F(10, 3 )
练习1.如图,点A是△DBC内一点,求BD得长。
分析:构造旋转相似,由基本图形可得出以下几种方法,求出BD=10.
练习2.如图,在△ABC中,∠ACB=90°,BC=2AC,F、G分别为AC、BC的中点,将△CFG绕点C顺时针旋转,直线AF与直线BG交于点I.
(1) 求证:AF⊥BG;
(2) 当旋转角小于90°时,求的值;
(3) 若AC=4,直接写出△ACI面积的最大值___________.
分析:
(3)需分析出I点轨迹,由A、C、I、B四点共圆可得∠AIC=∠ABC,又AC=4,定边定角得I轨迹为圆弧。
练习3.将等腰Rt△ABC和等腰Rt△ADE按图1方式放置,∠A=90°,AD边与AB边重合,AB=2AD=4.将△ADE绕点A逆时针旋转(旋转角不超过180°),BD的延长线交直线CE于点P.
(1)如图2,BD与CE的数量关系是___________,位置关系是___________;
(2)在旋转的过程中,当AD⊥BD时,求CP的长;
(3)当点D落在BA的延长线上时,求点P所经过的路径的长.
分析:
(1)BD=CE BD⊥CE
(2)∵BD⊥CE,AD⊥BD,∴∠ADP=∠DPE=90°
又∠DAE=90°,AD=AE,∴四边形ADPE为正方形
∵AB=2AD=4,∴PE=AD=2
∴CE=BD==2
∴CP=2-2
(3)取BC中点O,连接OA、OP
∵在旋转过程中,BD⊥CE,∴∠BPC=90°
∴OP= BC=2
∴点P的运动路径是以O为圆心、半径为2的一段圆弧
即△ABC外接圆的一部分
则∠AOP=2∠ABP
易知点D在以A为圆心、半径为2的半圆上运动
当BP与半圆A相切于点D时,∠ABP最大,从而∠AOP最大
∵AD= AB,∴∠ABP=30°,∴∠AOP=60°
即当△ADE从初始位置旋转60°时,点P沿圆弧从A点运动到∠AOP=60°
当△ADE继续旋转,直至点D落在BA的延长线上时,∠ABP=0°,∠AOP=0°
∴点P从∠AOP=60°处又回到A点
∴点P所经过的路径的长为:2×=
A
E
D
B
C
A
E
D
B
C
A
E
D
B
C
A
E
B
C
图1
图2
D
A
D
B
C
E
P
A
E
B
C
D
O
P
同课章节目录
