人教高中数学选修4-4第二讲2.1.1参数方程普通方程互化课件(28张)
文档属性
| 名称 | 人教高中数学选修4-4第二讲2.1.1参数方程普通方程互化课件(28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-10 12:48:56 | ||
图片预览








文档简介
第2课时 参数方程和普通方程的互化
第二讲 一 曲线的参考方程
学习目标
1.了解参数方程化为普通方程的意义.
2.掌握参数方程化为普通方程的基本方法.
3.能根据参数方程与普通方程的互化灵活解决问题.
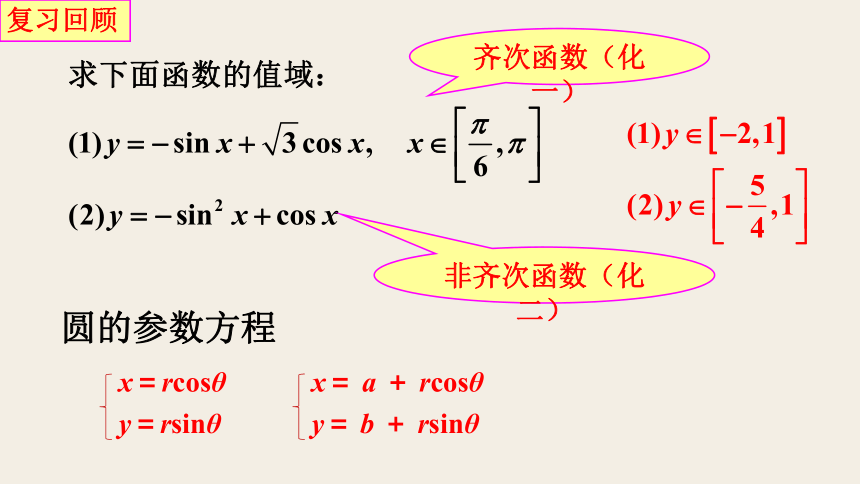
复习回顾
齐次函数(化一)
非齐次函数(化二)
x=rcosθ
y=rsinθ
x= a + rcosθ
y= b + rsinθ
圆的参数方程
1. 运用圆的参数方程,可以将相关问题转化为三角函数问题,利用三角函数知识解决问题.
反思与感悟
思考2
把参数方程化为普通方程的关键是什么?
答案
答案 关键是消参数.
(1)曲线的普通方程和参数方程的互相转化
①曲线的参数方程和普通方程是曲线方程的不同形式.一般地,可以通过
_________ 而从参数方程得到普通方程;
②如果知道变数x,y中的一个与参数t的关系,例如 ,把它代入普通方程,求出另一个变数与参数的关系 ,那么
梳理
就是曲线
的参数方程.
消去参数
x=f(t)
y=g(t)
(2)参数方程化为普通方程的三种常用方法
①代入法:利用解方程的技巧求出参数t,然后代入消去参数;
②三角函数法:利用三角恒等式消去参数;
③整体消元法:根据参数方程本身的结构特征,从整体上消去.
特别提醒:化参数方程为普通方程F(x,y)=0,在消参过程中注意变量x,y的取值范围,必须根据参数的取值范围,确定f(t)和g(t)的值域得x,y的取值范围.
例1 将下列参数方程化为普通方程,并判断曲线的形状.
类型一 参数方程化为普通方程
得y=-2x+3(x≥1),这是以(1,1)为端点的一条射线.
所以所求的方程为x+y=1(x≠-1,y≠2).
方程表示直线(去掉一点(-1,2)).
所以x+y=1(x≠-1,y≠2). 方程表示直线(去掉一点(-1,2)).
消去参数方程中参数的技巧
(1)加减消参数法:如果参数方程中参数的符号相等或相反,常常利用两式相减或相加的方法消去参数.
(2)代入消参数法:利用方程思想,解出参数的值,代入另一个方程消去参数的方法,称为代入消参法,这是非常重要的消参方法.
(3)三角函数式消参数法:利用三角函数基本关系式sin2θ+cos2θ=1消去参数θ.
反思与感悟
跟踪训练1 将下列参数方程化为普通方程.
∴(x-1)2+y=cos2θ+sin2θ=1, 即y=-(x-1)2+1(0≤y≤1),
∴普通方程为y=-x2+1(0≤y≤1).
(2) 由x=sin θ-cos θ,得x2=1-2sin θcos θ=1-sin 2θ,
∴x2+y=1, ∴普通方程为y=-x2+1(0≤y≤1).
例2 根据所给条件,把曲线的普通方程化为参数方程.
类型二 普通方程化为参数方程
(2)x2-y+x-1=0,x=t+1.(t为参数)
(2)将x=t+1代入x2-y+x-1=0,得
y=x2+x-1=(t+1)2+t+1-1=t2+3t+1,
(1)普通方程化为参数方程时,选取参数后,要特别注意参数的取值范围,它将决定参数方程是否与普通方程等价.
(2)参数的选取不同,得到的参数方程是不同的.
反思与感悟
跟踪训练2 已知曲线的普通方程为4x2+y2=16.
(1)若令y=4sin θ(θ为参数),如何求曲线的参数方程?
解 (1)把y=4sin θ代入方程,得到4x2+16sin2θ=16,
于是4x2=16-16sin2θ=16cos2θ,∴x=±2cos θ.
(2)若令y=t(t为参数),如何求曲线的参数方程?若令x=2t(t为参数),如何求曲线的参数方程?
(2)将y=t代入普通方程4x2+y2=16,得4x2+t2=16,
因此,椭圆4x2+y2=16的参数方程是
例3 已知x,y满足圆C:x2+(y-1)2=1的方程,直线l的参数方程为
类型三 参数方程与普通方程互化的应用
(1)求3x+4y的最大值和最小值; (2)若P(x,y)是圆C上的点,求P到直线l的最小距离,并求此时点P的坐标.
∴3x+4y的最大值为9,最小值为-1.
(1)参普互化有利于问题的解决,根据需要,合理选择用参数方程还是普通方程.
(2)解决与圆有关的最大值,最小值时,通常用圆的参数方程,将问题转化为三角函数的最大值,最小值问题.
反思与感悟
跟踪训练3 在直角坐标系xOy中,直线l的方程为x-y+4=0.以原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
.(1)求直线l的极坐标方程,曲线C的直角坐标方程;(2)若点P是曲线C上任意一点,P点的直角坐标为(x,y),求x+2y的最大值和最小值.
解 (1)直线l的方程为x-y+4=0,因为x=ρcosθ,y=ρsinθ,
所以l的极坐标方程为ρcosθ-ρsinθ+4=0.
所以ρ2-4ρcosθ-4ρsinθ+6=0,
因为ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
所以曲线C的直角坐标方程为(x-2)2+(y-2)2=2.
1.若点P在曲线ρcosθ+2ρsinθ=3上,其中0≤θ≤ ,ρ>0,则点P的轨迹是( )
A.直线x+2y=3 B.以(3,0)为端点的射线
C.圆(x-1)2+y2=1 D.以(1,1),(3,0)为端点的线段
D
2.将参数方程 (θ为参数)化成普通方程为( )
A.y=x-2 B.y=x+2
C.y=x-2(2≤x≤3) D.y=x+2(0≤y≤1)
解析 由x=2+sin2θ,得sin2θ=x-2,代入y=sin2θ,
∴y=x-2.
又sin2θ=x-2∈[0,1],∴x∈[2,3].
C
y2=x+1(-1≤x≤1)
圆
解析 x2+y2=(3cos φ+4sin φ)2+(4cos φ-3sin φ)2=25,表示圆.
x2-y=2(y≥2)
规律与方法
1.参数方程和普通方程的互化
参数方程化为普通方程,可通过代入消元法和三角恒等式消参法消去参数方程中的参数,通过曲线的普通方程来判断曲线的类型,研究曲线的性质.
由普通方程化为参数方程要选定恰当的参数,寻求曲线上任一点M的坐标x,y和参数的关系,根据实际问题的要求,可以选择时间、角度、线段长度、直线的斜率、截距等作为参数.
2.同一问题参数的选择往往不是惟一的,适当地选择参数,可以简化解题的过程,降低计算量,提高准确率.
3.参数方程与普通方程的等价性
把参数方程化为普通方程后,很容易改变变量的取值范围,从而使得两种方程所表示的曲线不一致,因此我们要注意参数方程与普通方程的等价性.
