21.1二次根式导学案
图片预览

文档简介
中小学教育资源及组卷应用平台
21.1二次根式导学案
课题 二次根式 单元 21 学科 数学 年级 九年级
知识目标 1.理解二次根式的概念。 2.通过讨论、交流,使学生学会分析二次根式的双重非负性及应用。
重点难点 重点:理解二次根式的概念。 难点:二次根式的双重非负性。
教学过程
知识链接 填一填 1.每一个正实数a有且只有 个平方根,其中一个平方根是 ,记作 ,称它为a的算术平方根,另一个平方根是 。 2.0的平方根是 ,记作 。 3.的平方根是 ,的算术平方根是 。 4.当x 时,的值是零 5.若,则 .
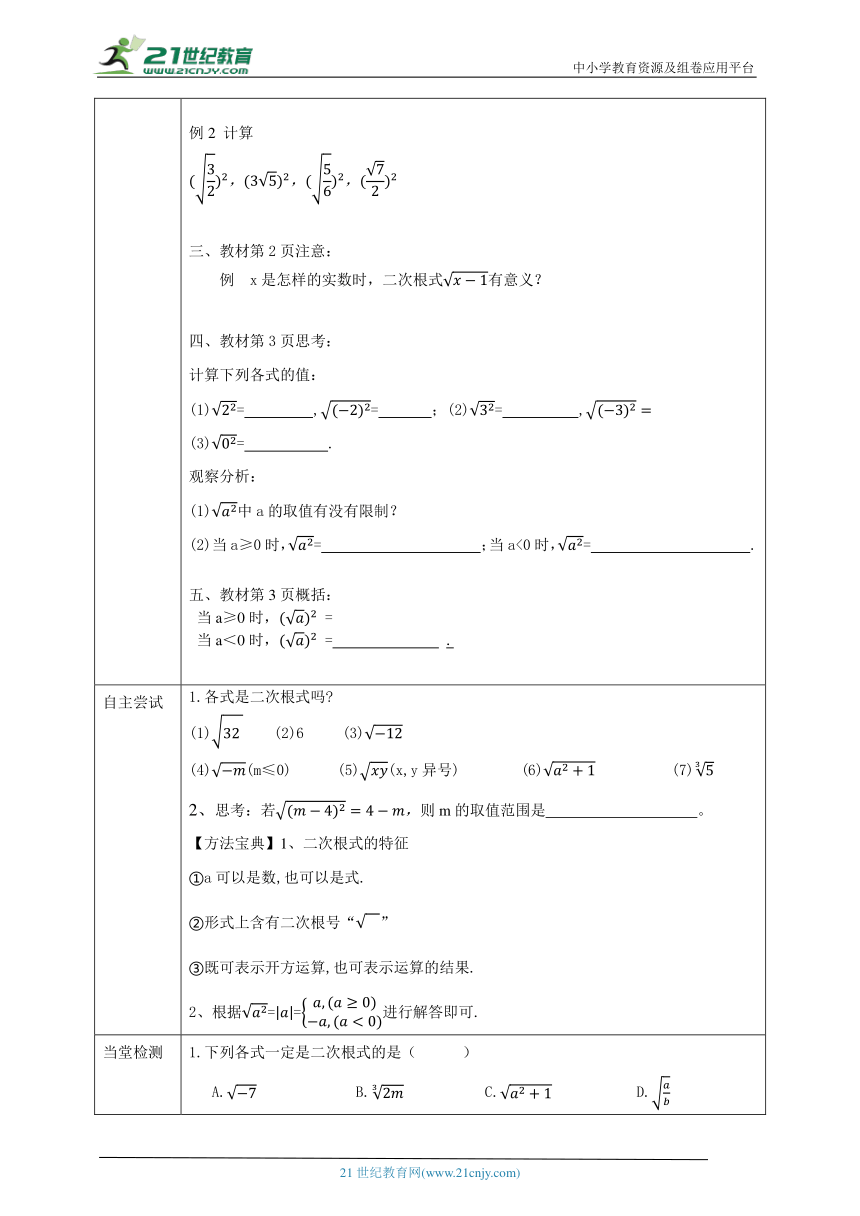
合作探究 一、教材第2页回顾: 表示什么? . . 二、教材第2页概括: 1. 叫做二次根式。 二次根式的概念有两个要点:一是从形式上看,应含有二次根号;二是被开方数的取值范围有限制:被开方数a必须是非负数. 二次根式表示为(a≥0),“”称为二次根号 讨论:①-1有算术平方根吗? ②0的算术平方根是多少? ③当a<0,有意义吗? 例1.下列式子,哪些是二次根式,哪些不是二次根式: ,, 归纳: 式子表示 。 表示 。 例2 计算 三、教材第2页注意: 例 x是怎样的实数时,二次根式有意义? 四、教材第3页思考: 计算下列各式的值: (1)= ,= ;(2)= , (3)= . 观察分析: (1)中a的取值有没有限制? (2)当a≥0时,= ;当a<0时,= . 五、教材第3页概括: 当a≥0时, = 当a<0时, = .
自主尝试 1.各式是二次根式吗 (1) (2)6 (3) (4)(m≤0) (5)(x,y异号) (6) (7) 2、思考:若则m的取值范围是 。 【方法宝典】1、二次根式的特征 ①a可以是数,也可以是式. ②形式上含有二次根号“” ③既可表示开方运算,也可表示运算的结果. 2、根据==进行解答即可.
当堂检测 1.下列各式一定是二次根式的是( ) A. B. C. D. 2.若2<a<3,则等于( ) A.5﹣2a B.1﹣2a C.2a﹣1 D.2a﹣5 3.若=1﹣x,则x的取值范围是( ) A.x>1 B.x≥1 C.x<1 D.x≤1 4.已知,则的值为( ) A. B.8 C. D.6 5. 若,则x=_______ ,y=___________ . 6.求使下列各式有意义的x的取值范围? (1) (2) (3) 拓展提高 已知、为实数,且,求的值.
小结反思 通过本节课的学习,你们有什么收获? 1.二次根式的概念。 2.二次根式的性质。 3.二次根式的化简.
参考答案: 当堂检测: 1、C 2、D 3、D 4、C 5、5, 6 6、(1)-2≤x≤ (2)x≤0且x≠-1 (3)x≠1 拓展提高 解:由题意得,,且. ∴, ∴. ∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
21.1二次根式导学案
课题 二次根式 单元 21 学科 数学 年级 九年级
知识目标 1.理解二次根式的概念。 2.通过讨论、交流,使学生学会分析二次根式的双重非负性及应用。
重点难点 重点:理解二次根式的概念。 难点:二次根式的双重非负性。
教学过程
知识链接 填一填 1.每一个正实数a有且只有 个平方根,其中一个平方根是 ,记作 ,称它为a的算术平方根,另一个平方根是 。 2.0的平方根是 ,记作 。 3.的平方根是 ,的算术平方根是 。 4.当x 时,的值是零 5.若,则 .
合作探究 一、教材第2页回顾: 表示什么? . . 二、教材第2页概括: 1. 叫做二次根式。 二次根式的概念有两个要点:一是从形式上看,应含有二次根号;二是被开方数的取值范围有限制:被开方数a必须是非负数. 二次根式表示为(a≥0),“”称为二次根号 讨论:①-1有算术平方根吗? ②0的算术平方根是多少? ③当a<0,有意义吗? 例1.下列式子,哪些是二次根式,哪些不是二次根式: ,, 归纳: 式子表示 。 表示 。 例2 计算 三、教材第2页注意: 例 x是怎样的实数时,二次根式有意义? 四、教材第3页思考: 计算下列各式的值: (1)= ,= ;(2)= , (3)= . 观察分析: (1)中a的取值有没有限制? (2)当a≥0时,= ;当a<0时,= . 五、教材第3页概括: 当a≥0时, = 当a<0时, = .
自主尝试 1.各式是二次根式吗 (1) (2)6 (3) (4)(m≤0) (5)(x,y异号) (6) (7) 2、思考:若则m的取值范围是 。 【方法宝典】1、二次根式的特征 ①a可以是数,也可以是式. ②形式上含有二次根号“” ③既可表示开方运算,也可表示运算的结果. 2、根据==进行解答即可.
当堂检测 1.下列各式一定是二次根式的是( ) A. B. C. D. 2.若2<a<3,则等于( ) A.5﹣2a B.1﹣2a C.2a﹣1 D.2a﹣5 3.若=1﹣x,则x的取值范围是( ) A.x>1 B.x≥1 C.x<1 D.x≤1 4.已知,则的值为( ) A. B.8 C. D.6 5. 若,则x=_______ ,y=___________ . 6.求使下列各式有意义的x的取值范围? (1) (2) (3) 拓展提高 已知、为实数,且,求的值.
小结反思 通过本节课的学习,你们有什么收获? 1.二次根式的概念。 2.二次根式的性质。 3.二次根式的化简.
参考答案: 当堂检测: 1、C 2、D 3、D 4、C 5、5, 6 6、(1)-2≤x≤ (2)x≤0且x≠-1 (3)x≠1 拓展提高 解:由题意得,,且. ∴, ∴. ∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
