人教版八年级数学下册第二十章 数据的分析测试题(一)含答案
文档属性
| 名称 | 人教版八年级数学下册第二十章 数据的分析测试题(一)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 187.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-10 15:58:54 | ||
图片预览

文档简介
第二十章 数据的分析测试题(一)
一、选择题(每小题3分,共30分)
1.11名同学参加数学竞赛初赛,他们的得分互不相同,按从高分录到低分的原则,取前6名同学参加复赛,现在小明同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的( )
A.平均数 B.中位数 C.众数 D.方差
2.某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分 B.82分 C.84分 D.86分
3.为迎接“义务教育均衡发展”检查,我市抽查了某校七年级8个班的班额人数,抽查数据统计如下:52,49,56,54,52,51,55,54,则这组数据的众数是( )
A.52和54 B.52 C.53 D.54
4.(2017年贺州) (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?071b2aec-89e6-424a-9bf4-25d659a10182" \t "_blank?)现有相同个数的甲、乙两组数据,经计算得:=,且=0.35,=0.25,比较这两组数据的稳定性,下列说法正确的是( )
A.甲比较稳定 B.乙比较稳定 C.甲、乙一样稳定 D. 无法确定
5.对于一组数据﹣1,﹣1,4,2,下列结论不正确的是( )
A.平均数是1 B.众数是﹣1 C.中位数是0.5 D.方差是3.5
6.某学习小组9名学生参加“数学竞赛”,他们的得分情况如下表:
人数(人) 1 3 4 1
分数(分) 80 85 90 95
那么这9名学生得分的众数和中位数分别是( )
A.90分,90分 B.90分,85分 C.90分,87.5分 D.85分,85分
7.一组数据1,5,7,x的众数与中位数相等,则这组数据的平均数是( )
A.6 B.5 C.4.5 D.3.5
8.图1所示是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A. 16小时,10.5小时 B. 8小时,9小时
C. 16小时,8.5小时 D. 8小时,8.5小时
9.已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是( )
A. 3,2 B. 3,4 C. 5,2 D. 5,4
10.已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中有一位同学的年龄登记错误,将14岁写成15岁.经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论正确的是( )
A. a<13,b=13 B. a<13,b<13 C. a>13,b<13 D. a>13,b=13
二、填空题(每小题3分,共18分)
11.对部分参加夏令营的中学生的年龄(单位:岁)进行统计,结果如下表:
年 龄 13 14 15 16 17 18
人 数 4 5 6 6 7 2
则这些学生年龄的众数是 .
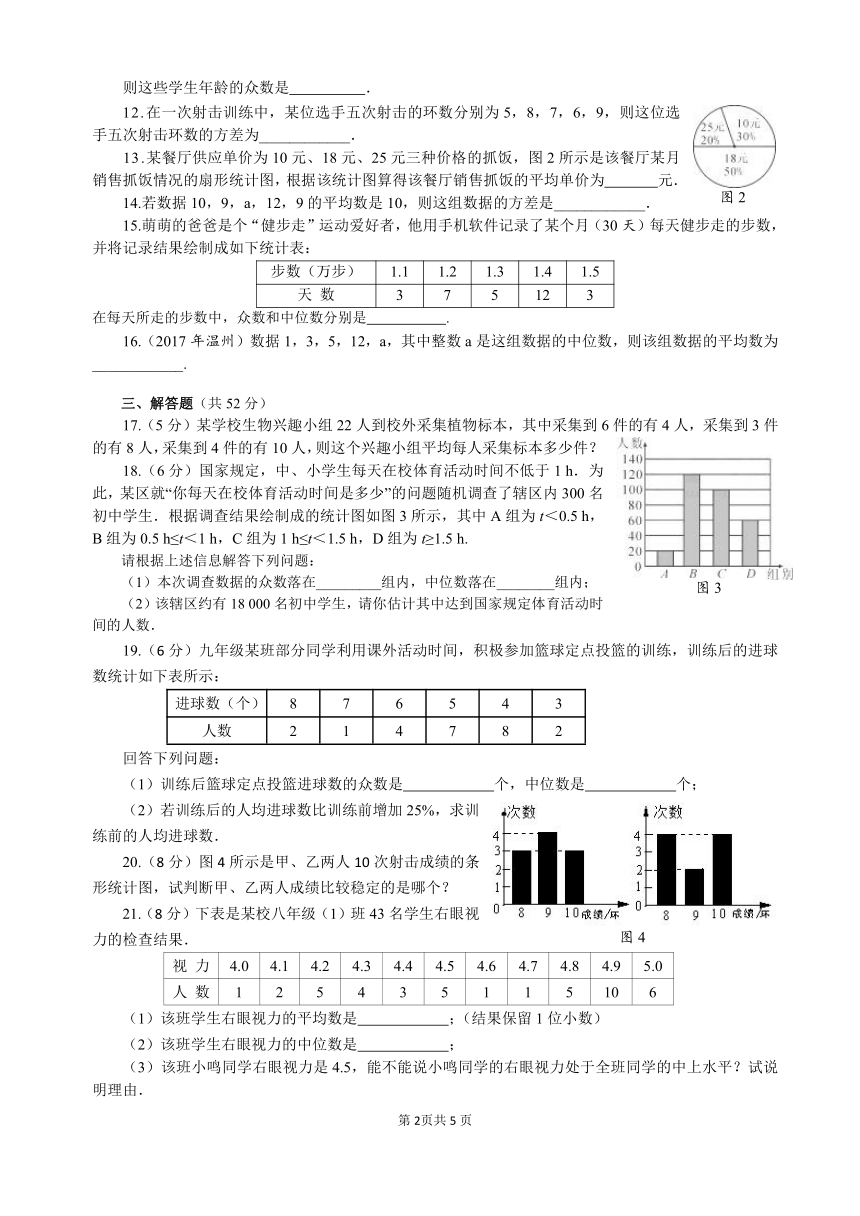
12.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为____________.
13.某餐厅供应单价为10元、18元、25元三种价格的抓饭,图2所示是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图算得该餐厅销售抓饭的平均单价为 元.
14.若数据10,9,a,12,9的平均数是10,则这组数据的方差是____________.
15.萌萌的爸爸是个“健步走”运动爱好者,他用手机软件记录了某个月(30天)每天健步走的步数,并将记录结果绘制成如下统计表:
步数(万步) 1.1 1.2 1.3 1.4 1.5
天 数 3 7 5 12 3
在每天所走的步数中,众数和中位数分别是 .
16.(2017年温州)数据1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数为____________.
三、解答题(共52分)
17.(5分)某学校生物兴趣小组22人到校外采集植物标本,其中采集到6件的有4人,采集到3件的有8人,采集到4件的有10人,则这个兴趣小组平均每人采集标本多少件?
18.(6分)国家规定,中、小学生每天在校体育活动时间不低于1 h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图3所示,其中A组为t<0.5 h,B组为0.5 h≤t<1 h,C组为1 h≤t<1.5 h,D组为t≥1.5 h.
请根据上述信息解答下列问题:
(1)本次调查数据的众数落在_________组内,中位数落在________组内;
(2)该辖区约有18 000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
19.(6分)九年级某班部分同学利用课外活动时间,积极参加篮球定点投篮的训练,训练后的进球数统计如下表所示:
进球数(个) 8 7 6 5 4 3
人数 2 1 4 7 8 2
回答下列问题:
(1)训练后篮球定点投篮进球数的众数是 个,中位数是 个;
(2)若训练后的人均进球数比训练前增加25%,求训练前的人均进球数.
20.(8分)图4所示是甲、乙两人10次射击成绩的条形统计图,试判断甲、乙两人成绩比较稳定的是哪个?
21.(8分)下表是某校八年级(1)班43名学生右眼视力的检查结果.
视 力 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人 数 1 2 5 4 3 5 1 1 5 10 6
(1)该班学生右眼视力的平均数是 ;(结果保留1位小数)
(2)该班学生右眼视力的中位数是 ;
(3)该班小鸣同学右眼视力是4.5,能不能说小鸣同学的右眼视力处于全班同学的中上水平?试说明理由.
组 别 平均分 中位数 方 差 合格率 优秀率
甲 组 6.8 a 3.76 90% 30%
乙 组 b 7.5 1.96 80% 20%
22.(9分)某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图表所示:
(1)求出成绩统计分析表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
23.(10分)某班九年级第二学期数学一共进行四次考试,小丽和小聪的成绩如下表:
姓 名 单元测验1 期中考试 单元测验2 期末考试
小 丽 85 75 95 85
小 聪 65 95 85 95
(1)请你通过计算这四次考试成绩的方差,比较谁的成绩比较稳定?
(2)若老师计算学生的学期总评成绩按照如下的标准:单元测验1占10%,期中考试占30%,单元测验2占10%,期末考试成绩占50%.请你通过计算,比较谁的学期总评成绩高?
附加题(20分,不计入总分)
24.我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
男生序号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
身高x(cm) 163 171 173 159 161 174 164 166 169 164
根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数和众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普通身高”的是哪几位男生?说明理由;
(3)若该年级共有280名男生,按(2)中选定标准,请你估算出该年级男生中具有“普通身高”的人数约有多少名?
(广东 雷成德)
第二十章 数据的分析测试题(一)参考答案
一、1. B 2. D 3. A 4. B 5. D 6. A 7. C 8. B 9. B 10. A
二、11. 17岁 12. 2 13. 17 14. 1.2 15. 1.4万步,1.35万步 16. 4.8或5或5.2
三、17. 解:×(6×4+3×8+4×10)=4(件),则该兴趣小组平均每人采集标本4件.
18. 解:(1)B C
(2)1 8 000×=9600(人).
答:达到国家规定体育活动时间的人数约有9600人.
19. 解:(1)4 5
(2)训练后人均进球数为=5(个).
设训练前的人均进球数为x,则(1+25%)x=5,解得x=4.
答:训练前的人均进球数为4个.
20. 解:甲的平均成绩为=(8×3+9×4+10×3)=9(环),方差为=[3×(8-9)2+4×(9-9)2+3×(10-9)2]=0.6;乙的平均成绩为=(8×4+9×2+10×4)=9(环),方差为=[4×(8-9)2+2×(9-9)2+4×(10-9)2]=0.8.
因为<,所以甲的成绩较稳定.
21. 解:(1)4.6
(2)4.7
(3)不能.
理由:因为小鸣同学右眼视力是4.5,小于中位数4.7,所以不能说小鸣同学的右眼视力处于全班同学的中上水平.
22. 解:(1)由折线统计图可知,甲组成绩从小到大排列为3,6,6,6,6,6,7,9,9,10,
所以其中位数a=6;乙组学生成绩的平均分b==7.2.
(2)因为甲组的中位数为6分,乙组的中位数为7.5分,而小英的成绩位于全班中上游,所以小英属于甲组学生.
(3)答案不唯一,如①乙组的平均分高于甲组,即乙组的总体平均水平高;②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定.
23. 解:(1)小丽四次考试成绩的平均分为×(85+75+95+85)=85(分),小聪四次考试成绩的平均分为×(65+95+85+95)=85(分).
=×[2×(85-85)2+(75-85)2+(95-85)2]=50,=×[(65-85)2+2×(95-85)2+(85-85)2]=150.
因为小丽和小聪的四次考试成绩的平均分相同,且<,所以小丽的成绩比较稳定.
(2)小丽的学期总评成绩为85×10%+75×30%+95×10%+85×50%=83(分),小聪的学期总评成绩为65×10%+95×30%+85×10%+95×50%=91(分),所以小聪的学期总评成绩高.
24. 解:(1)平均数为(163+171+173+159+161+174+164+166+169+164)=166.4(cm);中位数为=165(cm);众数为164(cm).
(2)选平均数作为标准:身高x满足166.4×(1-2%)≤x≤166.4×(1+2%),即163.072≤x≤169.728时为“普通身高”,此时⑦⑧⑨⑩男生的身高具有“普通身高”;
选中位数作为标准:身高x满足165×(1-2%)≤x≤165×(1+2%),即161.7≤x≤168.3时为“普通身高”,此时①⑦⑧⑩男生的身高具有“普通身高”;
选众数作为标准:身高x满足164×(1-2%)≤x≤164×(1+2%),即160.72≤x≤167.28时为“普通身高”,此时①⑤⑦⑧⑩男生的身高具有“普通身高”.
(3)以平均数作为标准,估计全年级男生中具有“普通身高”的人数约为280×=112(人);以中位数作为标准,估计全年级男生中具有“普通身高”的人数约为280×=112(人);以众数作为标准,估计全年级男生中具有“普通身高”的人数约为280×=140(人).
图2
图3
图4
图5
第4页共5页
