第三章 图形的平移与旋转综合测评 (含答案)
文档属性
| 名称 | 第三章 图形的平移与旋转综合测评 (含答案) | 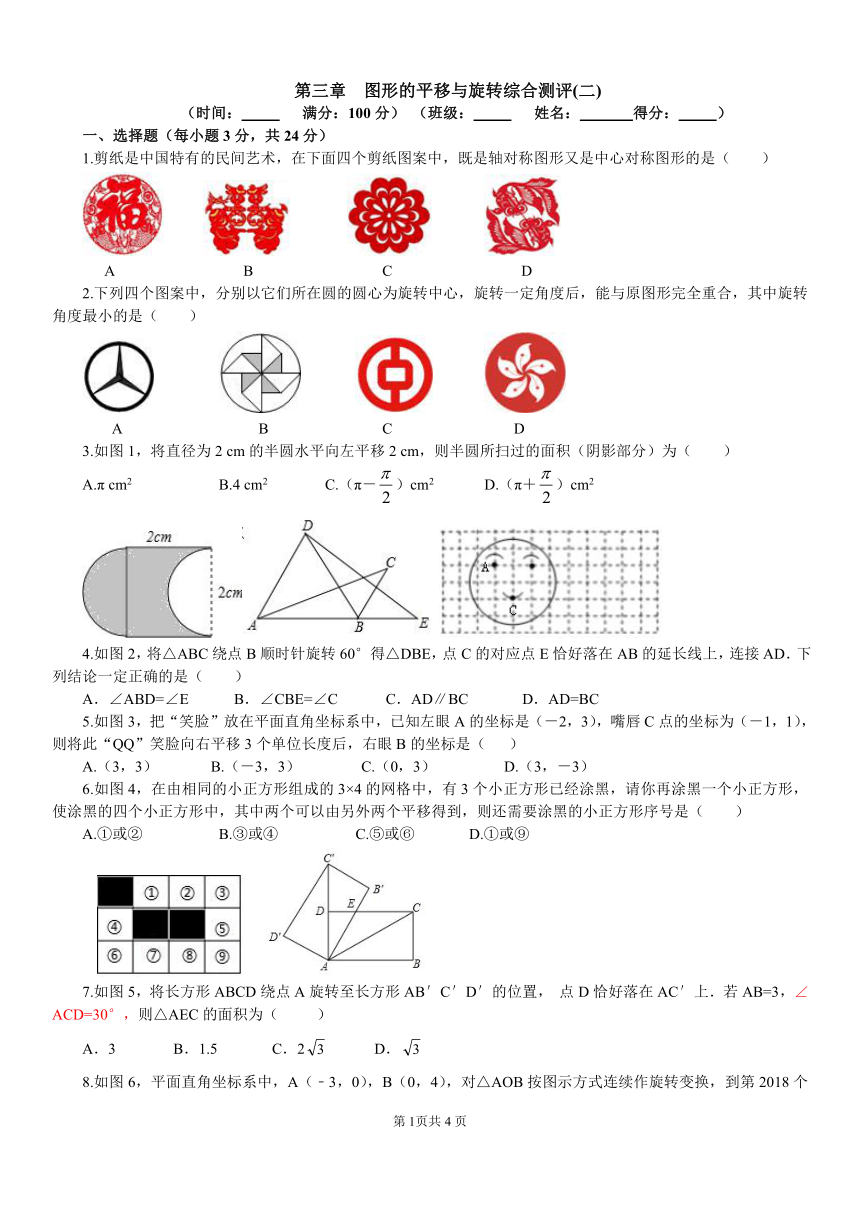 | |
| 格式 | zip | ||
| 文件大小 | 326.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-10 16:07:45 | ||
图片预览

文档简介
第三章 图形的平移与旋转综合测评(二)
(时间: 满分:100分) (班级: 姓名: 得分: )
一、选择题(每小题3分,共24分)
1.剪纸是中国特有的民间艺术,在下面四个剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列四个图案中,分别以它们所在圆的圆心为旋转中心,旋转一定角度后,能与原图形完全重合,其中旋转角度最小的是( )
A B C D
3.如图1,将直径为2 cm的半圆水平向左平移2 cm,则半圆所扫过的面积(阴影部分)为( )
A.π cm2 B.4 cm2 C.(π-)cm2 D.(π+)cm2
4.如图2,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD.下列结论一定正确的是( )
A.∠ABD=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC
5.如图3,把“笑脸”放在平面直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则将此“QQ”笑脸向右平移3个单位长度后,右眼B的坐标是( )
A.(3,3) B.(-3,3) C.(0,3) D.(3,-3)
6.如图4,在由相同的小正方形组成的3×4的网格中,有3个小正方形已经涂黑,请你再涂黑一个小正方形,使涂黑的四个小正方形中,其中两个可以由另外两个平移得到,则还需要涂黑的小正方形序号是( )
A.①或② B.③或④ C.⑤或⑥ D.①或⑨
7.如图5,将长方形ABCD绕点A旋转至长方形AB′C′D′的位置, 点D恰好落在AC′上.若AB=3,∠ACD=30°,则△AEC的面积为( )
A.3 B.1.5 C.2 D.
8.如图6,平面直角坐标系中,A(﹣3,0),B(0,4),对△AOB按图示方式连续作旋转变换,到第2018个三角形时,点A的对应点的坐标为( )
A.(8073,4) B.(8073,0) C.(8073,3) D.(8070,0)
二、填空题(每小题4分,共32分)
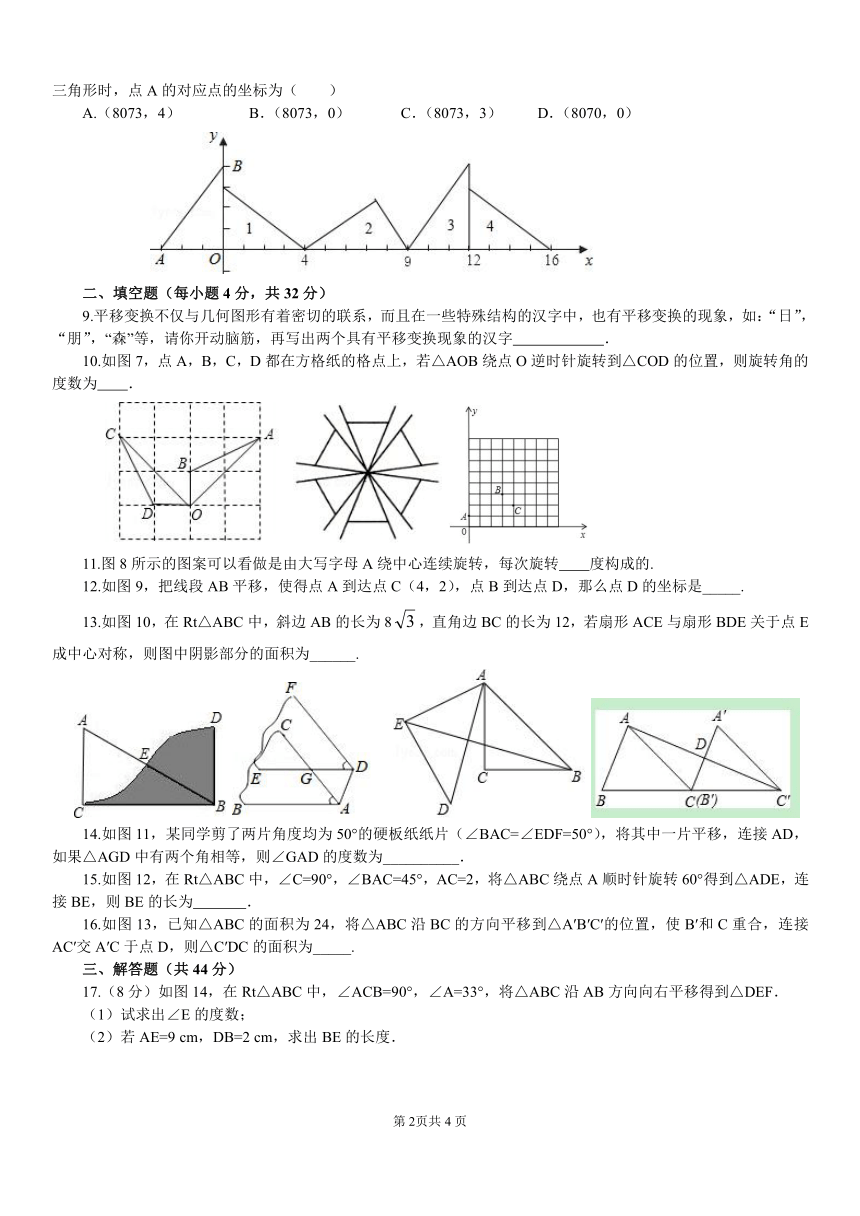
9.平移变换不仅与几何图形有着密切的联系,而且在一些特殊结构的汉字中,也有平移变换的现象,如:“日”,“朋”,“森”等,请你开动脑筋,再写出两个具有平移变换现象的汉字 .
10.如图7,点A,B,C,D都在方格纸的格点上,若△AOB绕点O逆时针旋转到△COD的位置,则旋转角的度数为 .
11.图8所示的图案可以看做是由大写字母A绕中心连续旋转,每次旋转 度构成的.
12.如图9,把线段AB平移,使得点A到达点C(4,2),点B到达点D,那么点D的坐标是_____.
13.如图10,在Rt△ABC中,斜边AB的长为8,直角边BC的长为12,若扇形ACE与扇形BDE关于点E成中心对称,则图中阴影部分的面积为______.
14.如图11,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连接AD,如果△AGD中有两个角相等,则∠GAD的度数为__________.
15.如图12,在Rt△ABC中,∠C=90°,∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,则BE的长为 .
16.如图13,已知△ABC的面积为24,将△ABC沿BC的方向平移到△A′B′C′的位置,使B′和C重合,连接AC′交A′C于点D,则△C′DC的面积为_____.
三、解答题(共44分)
17.(8分)如图14,在Rt△ABC中,∠ACB=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(1)试求出∠E的度数;
(2)若AE=9 cm,DB=2 cm,求出BE的长度.
18.(10分)如图15,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)经过平移,使△ABC的顶点A与坐标原点O重合,画出平移后的△OB′C′;
(2)已知△ABC内部一点G的坐标为(a,b),请直接写出点G在△OB′C′中的对应点的坐标(分别用含a,b的代数式表示);
(3)将△ABC绕坐标原点O逆时针旋转90°,得到△A″B″C″,画出△A″B″C″.
19.(12分)如图16-①,网格中每个小正方形的边长为1,请你认真观察图中三个网格中阴影部分构成的图案,解答下列问题:
(1)这三个图案都具有的特征:都是_____对称图形,都不是____对称图形;
(2)请在图16-②中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图20-①中所给出的图案相同.
20.(14分)将两块全等的含30°角的三角尺按图17-①所示的方式摆放在一起,它们较短的直角边BC=EC=3.
(1)将△ECD沿直线l向左平移到图17-②的位置,使点E′落在AB上,求CC′的长度;
(2)将△ECD绕点C逆时针旋转到图17-③的位置,使点E′落在AB上,求△ECD绕点C旋转的度数;
(3)将△ECD沿直线AC翻折到图17-④的位置,ED′与AB相交于点F,求证:AF=FD′.
(广东 吴丽)
第三章 图形的平移与旋转综合测评(二)参考答案
一、1.C 2.D 3.B 4.C 5.A 6.D 7.D 8.B
二、9.答案不唯一,如羽、圭、品、晶等 10.90° 11.60 12.(7,4) 13.24
14.50°或80°或65° 15.+ 16.12
三、17.解:(1)因为∠ACB=90°,∠A=33°,所以∠B=∠ACB﹣∠A=57°.
因为△ABC平移得到△DEF,所以∠E=∠B=57°.
(2)因为△ABC平移得到△DEF,所以AB=DE.所以AD=BE.
所以AE=AD+BD+BE=BE+2+BE=9,解得BE=3.5 cm.
18.解:(1)△OB′C′如图所示.
(2)点A先向右平移2个单位长度,再先向下平移3个单位长度可得到点O,所以点G在△OB′C′中对应点的坐标为(a+2,b-3).
(3)△A″B″C″如图所示.
19. (1)中心 轴
(2)略.
20.(1)解:由平移知,C′E′∥AC,C′E′=CE=3,所以∠BE′C′=∠A=30°.
因为BC=EC=3. 在Rt△BC′E′中,∠BE′C′=30°,所以BE′=2BC′.所以BE′2﹣BC′2=C′E′2,即4BC′2﹣BC′2=9,解得BC′=.所以CC′=BC﹣BC′=3-.
(2)解:因为∠ABC=60°,BC=CE′=3,AB=6,所以△E′BC是等边三角形.所以∠BCE′=60°.
所以∠ECE′=∠ACB-∠BCE′=90°-60°=30°,即△ECD绕点C旋转的度数是30°.
(3)证明:因为AE=AC﹣EC,D′B=D′C﹣BC,AC=D′C,EC=BC,所以AE=D′B.又因为∠AEF=∠D′BF=180°﹣60°=120°,∠A=∠BD′F=30°,所以△AEF≌△D′BF.所以AF=FD′.
①
②
图16
第4页共4页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
